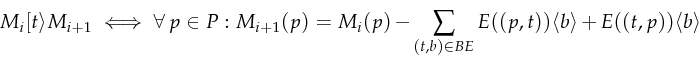| Home | Papers | Reports | Projects | Code Fragments | Dissertations | Presentations | Posters | Proposals | Lectures given | Course notes |
| << 11. Asynchronous Fractal Calculation | 13. Petrinet Design of a Whiteboard Voting System >> |
12. PetrinetsWerner Van Belle1 - werner@yellowcouch.org, werner.van.belle@gmail.com Abstract : Investigates the use of Petri-nets in distributed open systems, which also happen to be concurrent systems. This exercise was given in 2002-2003
Reference:
Werner Van Belle; Petrinets; |
1 Documented interfaces
Programming distributed systems is not easy because
- distributed systems are inherent concurrent systems, in which all too often multiple sessions have to be managed.
- one has to take into account the possibility of failures at virtually every possible moment.
A Petri-net is a drawing that formally and statically describes the possibilities and impossibilities of a system at runtime. In comparison to MSC's they fully describe the behavior which makes them perfectly suitable to do all kinds of static checking. For instance, can the system deadlock, will it stay running, what can happen if an error occurs and other questions can be answered automatically.
There are a lot of varieties of Petri-nets. For all practical purposes colored Petri-nets should be used, however, because it might be too much at once, we will first introduce elementary Petri-nets. Elementary nets offer a formalism that is relatively easy to explain and naturally extends to colored Petri-nets. A second reason why we introduce elementary nets is that all existing Petri-net formalisms are based upon the elementary ones.
2 Elementary Place/Transition Nets
2.1 Non-counting semaphore
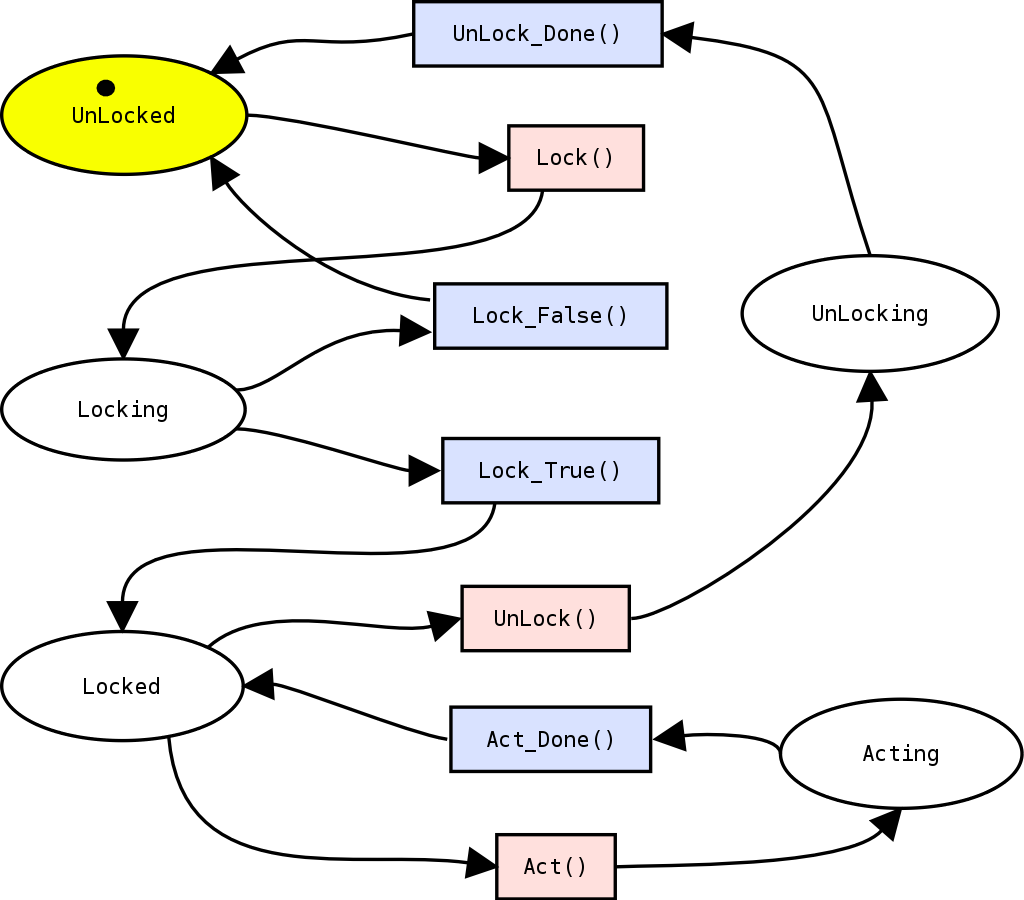
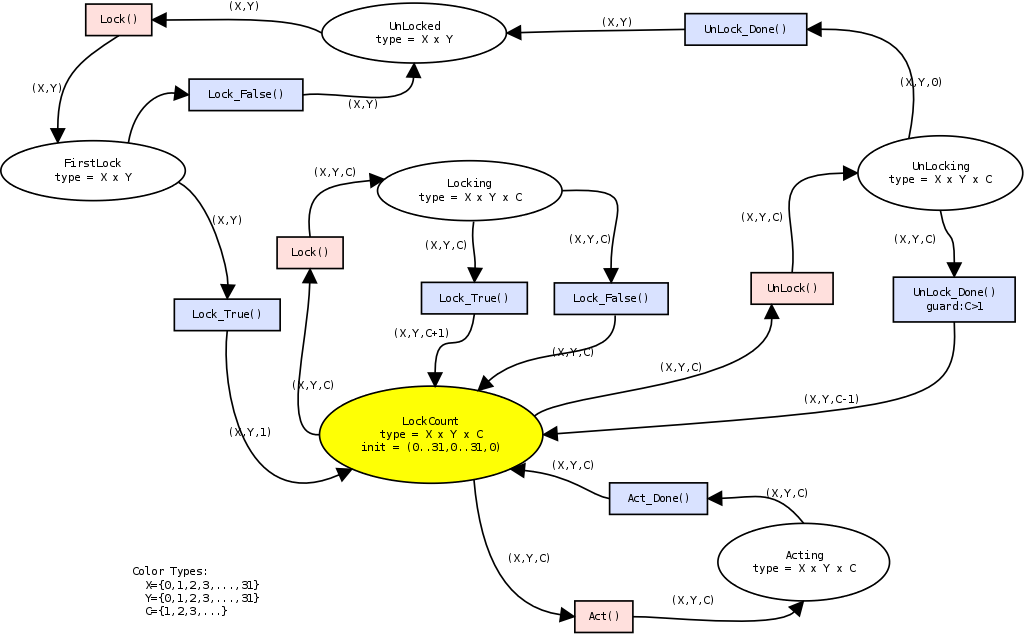
Petri-nets are drawn as box/circle diagrams. Figure 1 is a Petri-net describing the behavior of a non-counting semaphore. Petri-nets have a number of concepts:
- Places: places represent the state of a system. In our example, these are the circles. The places are unlocked, unlocking, locking, locked and acting. It is perfectly possible to have a Petri-net in which multiple places contain a token. Token can be moved from one place to another by transitions, however some rules should be considered:
- Tokens: A place can have zero, one or more tokens. Simple Petri-nets only have boolean tokens. A token is either there or is not there. In our example only the unlocked place contains a token. Tokens which contain values will be discussed when we describe colored Petri-nets.
- Transitions: A transition specifies how a token is replaced from one place to another. In our example, we have the transitions: UnlockDone, Lock, LockFalse, LockTrue, Unlock, ActDone and Act. A transition can be either enabled or disabled. If all the arcs coming into a transition offer a token the transition is enabled. In our case only the transition Lock is enabled because the only incoming arc from Unlocked offers a token. The transition Unlock is not enabled since there is no token at Locked. When a transition is executed all offered tokens are taken away from their place and transferred to all the places which receive an arc from this transition. If we would execute the transition Lock the token would be replaced from Unlocked to Locking. Afterward the transition LockFalse and LockTrue will be enabled. A transition of a P/T net is enabled only when all of its input-places offer a token and all its output places are empty.
- Marking: The marking of a Petri-net contains all the places that contain a certain token. The marking is in fact the global state of a Petri-net.
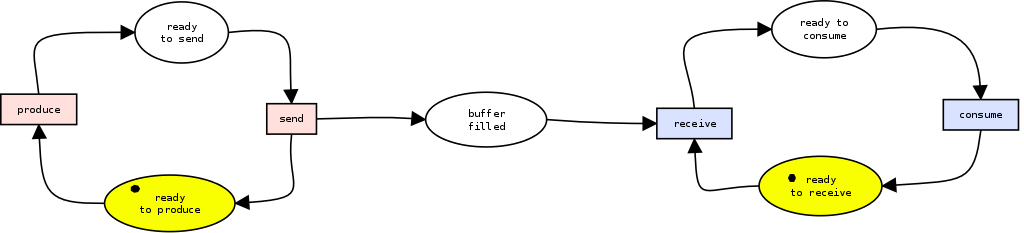
2.2 Producer/Consumer Example
Figure 2 is another P/T net. It describes the behavior of two actors. The first actor is a producer of data, the second is a consumer of data. In the above example, the only two enabled transitions are produce and receive. The above Petri-net is an illustration of how well Petri-nets can be combined.
To analyze the concurrency behavior of the above system, we can say that the consumer is only alive when the receive operation is alive. This is the case, only when the producer is alive and since this is also the case, the Petri-net in general is alive. The same counts for deadlock-freedom. The producer is deadlock-free if the place buffer filled can contain a token in all possible futures. This is again the case because the producer is alive and does not depend on anybody else.
2.3 A Note on implementation
Petri-nets can be implemented on control-flow machines, that is, machines with a 'fetch', 'execute', 'store', architecture. To do so one needs to keep a marking in working memory, to which all current transition are tested to make a step. The current marking in the working memory is then replaced by the new marking.1 However fast in execution, a typical control flow machine suffers from one enormous bottleneck: the memory access: since every single Petri-net step has to fetch and store data in the main working memory, Petri-nets are difficult to map efficiently to commonly used hardware.
Nevertheless, in the past, data-flow machines have been build which are much more efficient in executing Petri-nets. A data-flow machine consists of a number of registers that holds tokens, a token is transferred from operation to operation. In a typical data-flow machine an operation has at most two input-registers and at most two output operations. The input registers are filled in by other instructions that wants to pass a token to this operation. The destination registers contain the addresses where to put the result. These addresses refer to the input registers of other operations. Every operation has also two signaling registers which are used to schedule the passing of tokens.
[Moo96] contains a description of a number of existing data-flow machines. Not so strangely the evolution of data-flow machines follows very closely the evolution of formal Petri-net models.
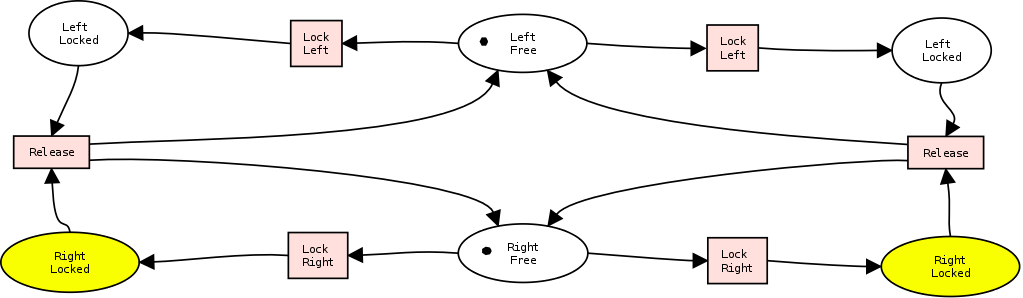
3 Exercise 1: Two Philosophers
Figure 3 shows two processes. The left process tries two lock two resources. The right process tries to do the same.
- Can you point out how a deadlock can arise ?
- How would you solve the problem?
4 Exercise 2: Call Semantics
- Draw a Petri-net of a regular call.
- How would you verify its behavior if one of both processes resets ?
5 Exercise 3: Java RMI
- Draw a Petri-net of the behavior of the server, down to the socket level. Make sure that at least two connections can be accepted
6 Colored P/T nets: CPNets
The previous description describes elementary place/transition Petri-nets (elementary PTNets). Although enough to describe the basic operation of a Petri-net they are barely useful in real life situations, unless we add some syntactical sugar. We will now explain how Petri-nets have been extended to be more practically useful. One of the first limitations one encounters is the lacks of values. Assume we want to extend the Petri-net in figure 1 to a nested locking strategy using an elementary PTNet.
To do so, with an elementary PTNet we would need to specify for every possible value of the lockcount variable a specific state, (e.g: we would have states 1, 2, 3, 4, 5, ...) and transitions in between them. This of course is a) no longer readable and as such not suitable as a specification language and is b) from a programmers point of view, not performant since we have a state explosion where it deems not necessary.
Another similar problem is the impossibility to easily replicate states. Consider the situation where we want to describe the interface behavior of a binary semaphore playfield. It is very simple to describe the behavior of a binary locking strategy for only a single square (see figure 1). The problem that now arises is how we should specify the same behavior for all squares on the playing field ? Without extensions the only thing we can do is write down a full exploded Petri-net, something that is clearly not manageable.
Therefore low level P/T nets were extended with the concept of colored tokens. Now instead of having only true/false tokens one can have tokens which contain a specific value (or color).
This small extension to Petri-nets complicates the formalism a lot. It is not clear when a certain transition is enabled: can we specifically check the color of a token or do we only check its presence. It is also not clear what should happen when a transition is executed, what color/value will the outgoing token(s) have ? Is it possible to send different tokens to different places ? Below we will explain how colored Petri-nets are defined.
6.1 Informal Discussion
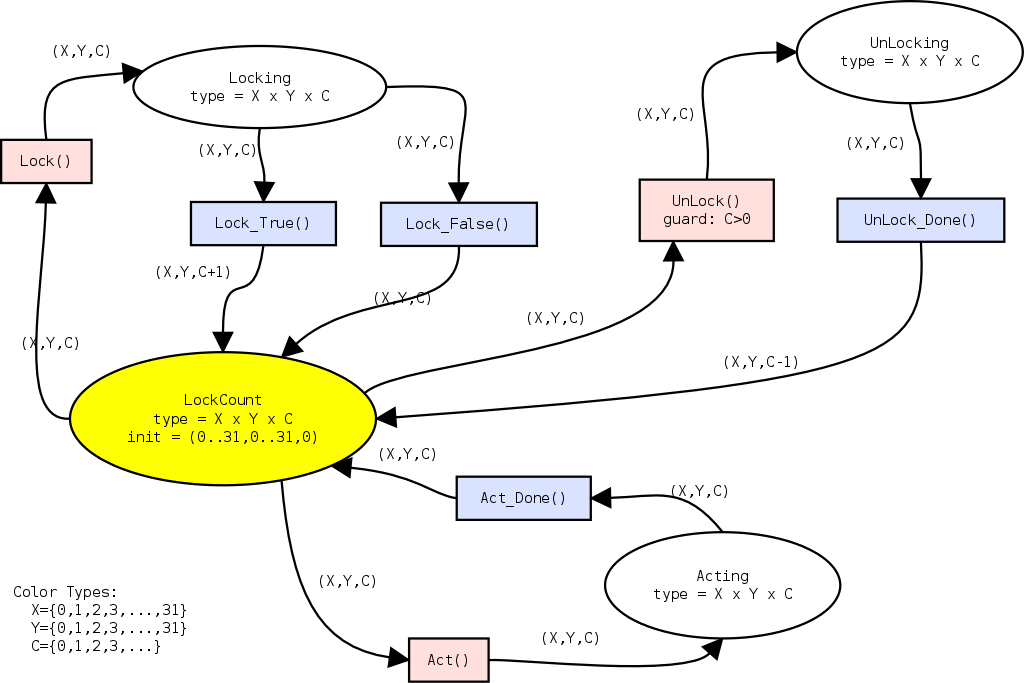
|
- First, every place has a type associated with it, a color set. This
type declares which possible values can be present at the given place.
For instance the Locking place has a type/color
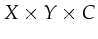 .
.
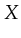 is the set of possible X values,
is the set of possible X values, 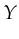 is the set of possible
Y values and
is the set of possible
Y values and 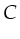 is the set of possible lockcounts, an infinite
set indeed. The possible colors of the tokens, or values for short,
at the locking place are tuples which belong to the set
is the set of possible lockcounts, an infinite
set indeed. The possible colors of the tokens, or values for short,
at the locking place are tuples which belong to the set
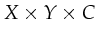 .
The values
.
The values 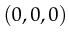 ,
, 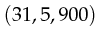 are valid tokens, while the values
are valid tokens, while the values
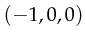 ,
, 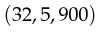 are invalid tokens.
are invalid tokens.
- Second, places can contain more than one token.
- Third, all arcs contain an expression which either describes the tokens
generated or the tokens to be matched. From the point of view of a
transition
- every incoming arc describes which tokens are looked for. For example,
the incoming arc on the 'Lock_True' transition needs a 3-tuple,
if one is available, such as
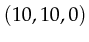 the variables
the variables 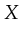 ,
, 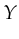 and
and 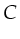 will be bound to the values present in the token/tuple. So,
will be bound to the values present in the token/tuple. So,
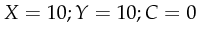 .
.
- every outgoing arc describes how new tokens are generated. If the
Lock_True transition is executed all incoming tokens are removed
from the input places and the output places receive newly created
tokens. For example, the outgoing arc of the Lock_True transition
contains the expression
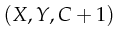 . Since the variables
. Since the variables 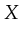 ,
, 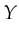 and
and 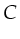 were bound to
were bound to 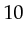 ,
, 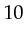 and
and 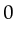 , the new token will be
, the new token will be
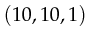 . This token will be put in the place LockCount.
. This token will be put in the place LockCount.
- every incoming arc describes which tokens are looked for. For example,
the incoming arc on the 'Lock_True' transition needs a 3-tuple,
if one is available, such as
- Fourth, some transitions can contain guards. A guard is an expression
which verifies whether the transition is enabled given a number of
input tokens. A guard is also an expression in some sort of language,
which will be described later. A guard should evaluate to true or
false. When a guard evaluates to true the transition is enabled, when
the guard evaluates to false but still all tokens are present the
transition is not enabled. For example, the transition Unlock has
a guard
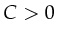 . Intuitively this means that a lock cannot be released
if the lock is not held. The outgoing arc of the UnlockDone transition
has an expression
. Intuitively this means that a lock cannot be released
if the lock is not held. The outgoing arc of the UnlockDone transition
has an expression 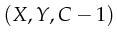 which decreases the lock counter with
one. Because we are sure that the incoming token has a lockcount
larger than
which decreases the lock counter with
one. Because we are sure that the incoming token has a lockcount
larger than 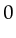 , the resulting token will always be in the set
, the resulting token will always be in the set
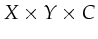 .
.
- Fifth, the expressions used within guards and on arcs can be chosen. However if one chooses a language too rigorous a lot of analyzing power is lost. The language we will choose will be described below.
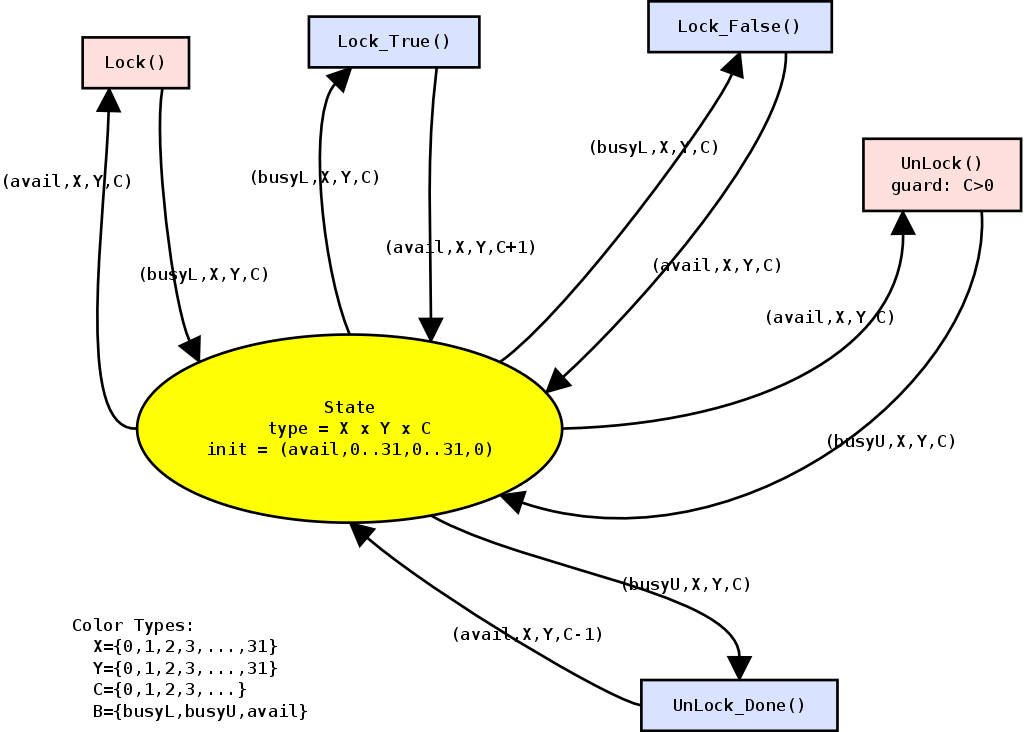
Given this, we can now clearly see the expressive power of Petri-nets. We can choose how much detail we include in our Petri-net. The Petri-net given in figure 4 only covers the locking of a single square with a lockcount. If we want we could add a session ID to check whether the incoming lock request is from the same one who already has obtained a lock. The fact that we do not need to specify this, without losing the ability to reflect over the behavior of the system is one of the greatest strengths of Petri-nets.
It is even possible to describe the same behavior with only one place.
Therefore we need to add another color ![]() which describes whether
a certain position is in busy locking (busyL), busy unlocking (busyU)
or available (avail). The associated Petri-net, without acting logic
for the sake of simplicity is pictured in 5.
On the other hand if we need to use this Petri-net in a larger context,
in which we only need to know whether a place is locked or unlocked
we can split the LockCount state of figure 4
in two as depicted in figure 6.
which describes whether
a certain position is in busy locking (busyL), busy unlocking (busyU)
or available (avail). The associated Petri-net, without acting logic
for the sake of simplicity is pictured in 5.
On the other hand if we need to use this Petri-net in a larger context,
in which we only need to know whether a place is locked or unlocked
we can split the LockCount state of figure 4
in two as depicted in figure 6.
|
6.2 The Expression Language
The formal definition of a colored Petri-net given earlier handled expressions as if they can be anything. Therefore we need to define what kind of expressions we will use. The expression language we will use has a syntax and semantics comparable to an enormously reduced variant of Scheme [SJ75]. The syntax:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Semantically speaking those expressions are straight forward. In the end everything evaluates to either a token or an integer. There are no other values to work with. If a compound statement is found, the arguments are evaluated in applicative order: they are all evaluated recursively, after that the operator is applied to the given values.
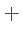 ,
, 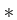 respectively adds, multiplies all given arguments.
respectively adds, multiplies all given arguments.
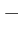 ,
, 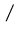 respectively subtracts, divides all arguments
respectively subtracts, divides all arguments 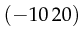 results in
results in 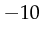 .
. 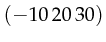 results in
results in 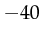 .
. 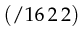 results in
results in 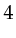 .
.
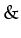 ,
, 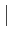 ,
, 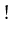 are logic operations. Something is considered to
be true if it is not zero.
are logic operations. Something is considered to
be true if it is not zero.
-
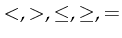 are comparison operators. They are not defined on
tokens.
are comparison operators. They are not defined on
tokens.
6.3 A Note on Implementation
Implementing an evaluator of CPNets seems trivial: instead of checking
whether a token is present and moving the token from the input places
to the output places we also have to check a guard. Unfortunately
it isn't that simple. Remember the formula 3,
if we want to know which transitions are enabled we must be able to
evaluate the right hand side of that expression. This means that we
must find a binding for which the guard (and accompanying expressions)
is satisfied. In contrast to an elementary net where we simply have
to check whether a token is present we now have to find out which
combination of tokens is suitable to satisfy the guard. Luckily,
when searching a suitable combination we only need to take into account
the set of all tokens present at places local to the transition under
investigation. This means that we don't have to check combinations
of tokens in places which are not immediately linked to the current
transition. This can be easily seen if we look at the two expressions
within formula 3. The first requirement,
there should be a ![]() , does not necessarily guarantee that
the values are present at the places local to t. In fact nothing says
where the values have to come from. It only guarantees that there
is a binding which satisfies the guard and which binds all necessary
values. The second part of the expression on the other hand
, does not necessarily guarantee that
the values are present at the places local to t. In fact nothing says
where the values have to come from. It only guarantees that there
is a binding which satisfies the guard and which binds all necessary
values. The second part of the expression on the other hand
![]() guarantees that all the values necessary to satisfy the guard are
present at the incoming places.
guarantees that all the values necessary to satisfy the guard are
present at the incoming places.
Practically this means that, when a transition has ![]() tokens in
total over all its input places (this set is called
tokens in
total over all its input places (this set is called ![]() and there
are
and there
are ![]() free variables (this set is called
free variables (this set is called ![]() we must try out
all permutations over X. If there are many tokens this number grows
fast. Hence we cannot check whether a transition is enabled in
we must try out
all permutations over X. If there are many tokens this number grows
fast. Hence we cannot check whether a transition is enabled in ![]() .
A second aspect to evaluating a Petri-net is knowing which transitions
have a chance to be enabled. If we start with an initial marking
.
A second aspect to evaluating a Petri-net is knowing which transitions
have a chance to be enabled. If we start with an initial marking ![]() we know that we only have to check the transitions immediately bound
to the places containing tokens. So we only need to check out
we know that we only have to check the transitions immediately bound
to the places containing tokens. So we only need to check out
![]() .
If a certain transition is selected to be executed we need to change
the marking from
.
If a certain transition is selected to be executed we need to change
the marking from ![]() to
to ![]() as specified in formula 4.
In human terms this equation transfers a certain amount of tokens
from the input place(s) to the output place(s). Thereby changing the
local states of all the input places and all the output places, formally
changing the state of
as specified in formula 4.
In human terms this equation transfers a certain amount of tokens
from the input place(s) to the output place(s). Thereby changing the
local states of all the input places and all the output places, formally
changing the state of
![]() . The transitions
connected to these places:
. The transitions
connected to these places:
![]() are the only ones who can possible change from disabled to enabled
(or vice versa).
are the only ones who can possible change from disabled to enabled
(or vice versa).
Because of this, it is important to have Petri-nets with enough distinct places: the amount of incoming tokens at a transition will be likely smaller if we have more places in a Petri-net. Also, evaluating the Petri-net can be much more oriented to a set of changed places as specified earlier. For example, a Petri-net as in figure 5 is very small, with only one place. Given the fact that the net is conservative2 and that we start with 3072 tokens, and there are 5 possible enabled transitions, we need to check out 15360 possibilities. This number rises exponentially with the number of input tokens taken by one transition. In comparison, consider the Petri-net in figure 4, we start with a token count of 1024 at place 'LockCount'. There are 3 possible output places so we need to check 3072 permutations.
Given the fact that we need to try out all permutations of incoming tokens we might start thinking of using something like a logic engine to evaluate a Petri-net. Indeed, it is very easy to write a Petri-net evaluator in something like Prolog. To do so one simply needs to translate the formal definition of a Petri-net to Prolog rules.
7 Exercise 4: Producer/Consumer
- Look at the producer/consumer Petri-net given earlier. If we would interpret this as a colored Petri-net what would be the difference ? How could we solve this problem ? Remember: a P/T-net only enables a transition if the output-places are empty. A CPNet does not impose this requirement.
8 Exercise 5: Compaction
- Draw the Petri-nets of the two dining philosophers as a colored Petri-net.
- Draw the Java RMI call as a colored Petri-net. Make sure that the same semantics are followed !
9 A word on formal analysis of Petri-nets
So, what is all this fuzz about Petri-nets ? It's a nice formalism and people like it, that's true, but why do a certain kind of people spend so many nights studying them ? To know how to answer these questions, and increase the universal IQ of the human race a tiny little bit, continue reading our intriguing saga, in which we introduce a number of very appealing properties of Petri-nets. Properties that those night-spending people like to call decidable, because they define a problem for which an answer can be calculated in some automatic way. In comparison to the answers given by mathematicians this is a tremendous improvement since they often end up simply proving that an answer exists to a certain problem without actually giving a way to find it. On the other hand, this so called decidability, often requires an exponential time to decide what they are supposed to decide... even if it is a simple question. This, given the fact that bare-to-the-metal programmers doesn't like exponential solutions to decide short answers, such as 'yes' or 'no', to not so large questions, such as for instance 'will this thing never stop ?', diminishes the fun a bit.
Luckily the past couple of decades, model-checking specialists came up with much better upper bounds to decide certain properties of Petri-nets... of course, only if the Petri-nets follows certain rules, which most computer scientists don't care about, they just like to think Petri-nets are easy to validate... :
- Boundedness: A Petri-net is bounded if the set of all possible
markings generated by a petri-net is finite. This property
is decidable, it is even possible to check whether the maximum amount
of tokens arriving at one place doesn't become larger than
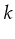 . In
this case a petri-net is called
. In
this case a petri-net is called 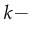 bounded.
bounded.
- Reachability: A marking
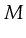 is reachable from marking
is reachable from marking 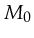 under Petri-net
under Petri-net 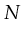 if there exists a sequence of transitions leading
from
if there exists a sequence of transitions leading
from 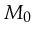 to
to 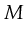 :
:
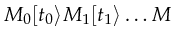 .
This is a very important property because it allows us to decide whether
a certain error condition can be met or not. Recursively we can define
this as follows:
.
This is a very important property because it allows us to decide whether
a certain error condition can be met or not. Recursively we can define
this as follows:
- Deadlock-freedom: A Petri-net is deadlock free if every reachable marking enables some transition. This property is decidable because it can be reduced to the reachability problem.
- Liveness: A Petri-net is alive if every transition can always occur again. Whether this is decidable or not is still an open question. This will turn out to be an important property, because it tells us that a certain concurrency strategy does not close any doors that shouldn't be closed.
- Homestate-problem: A Petri-net has a home state
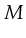 if this
marking can be reached from every other marking. The question to decide
now is whether a given marking is a homestate for a certain Petri-net.
This problem has shown to be decidable.
if this
marking can be reached from every other marking. The question to decide
now is whether a given marking is a homestate for a certain Petri-net.
This problem has shown to be decidable.
- Non-Termination: The question whether a Petri-net will never terminate is generally speaking undecidable.
A reachability analysis of a Petri-net gives an answer how whether we can reach a certain marking or not, often information is included how this marking can be reached. Reachability is decidable [EN94]. However it might take a look time. Generally, it is NP-complete. However for a lot of Petri-net classes better results exist. For instance:
- If the petri-net is symmetric then the reachability problem
is EXPTIME-complete (see glossary). A petri-net is symmetric when
for every transition
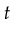 there is a transition
there is a transition 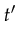 that undoes
the effect of the first transition and returns back to the original
marking. This is a property which is often found in concurrency interfaces.
Once a lock is obtained it is possible to release it again. However,
aside from this intuition nothing guarantees that the petri-net also
exhibits this behavior.
that undoes
the effect of the first transition and returns back to the original
marking. This is a property which is often found in concurrency interfaces.
Once a lock is obtained it is possible to release it again. However,
aside from this intuition nothing guarantees that the petri-net also
exhibits this behavior.
- If the petri-net is conflict-free and bounded then reachability is decidable in P. (see glossary) A Petri-net is bounded when there is a maximum to the number of possible tokens present at a certain place. A Petri-net is conflict-free if for every possible marking the net is persistent. A petri-net is persistent if for every place with more than one enabled output transition, the execution of one transition does not disable the other transition. In the case of concurrency interfaces this is highly likely because normally multiple transitions will not be enabled at once and the amount of resources remains fixed.
- Reachability in timed petri-nets is NP-complete [LLPY97,BP96]).
- Our expression language is no standard language so we don't exactly know whether all these proofs holds with the given language. I assume it does, because the language does not allow destructive operations, nor does it have access to a memory, nevertheless we cannot be sure of this.
- Colored petri-nets makes all these formal approaches a bit problematic. Expanding a colored petri-net to a simple petri-net may require an infinite explosion, hence all these decidability criteria needs to be investigated again.
Another approach is the construction of an unfolding of a Petri-net [ERV96]. An unfolding of a Petri-net is a new petri-net, usually with an infinite but simpler structure. McMillan proposed an algorithm for the construction of a finite initial prefix of the petri-net, which contains full reachability information. However, this information is difficult to generate, and can take a long time. Therefore we didn't investigate this track further.
To ease the pain of deciding reachability, other tools are possible. For instance it is possible to exploit symmetry between states by only looking at one side of the symmetry. To feed the reader's intuition: within a dining philosopher petri-net there is a 4 way symmetry. There is no need in trying out every philosopher, which reduces the state explosion drastically. how this can be done in practice is described in detail in [Jør].
10 Formal definition Of Elementary P/T Nets
We will now formally define what a Petri-net is. This definition is
loosely based upon [Rei00]. Formally speaking, an
elementary PTNet is a triple ![]() whereby
whereby ![]() contains all
the states,
contains all
the states, ![]() contains all the transitions and
contains all the transitions and ![]() contains the
flow relation, that is the linkage between states and transitions.
contains the
flow relation, that is the linkage between states and transitions.
![]() ,
, ![]() and
and ![]() are finite sets.
are finite sets.
-
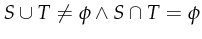
-
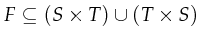
-
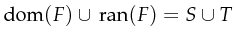
whereby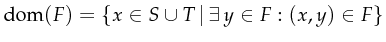
and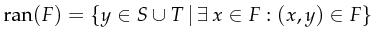
 the places of Petri-net
the places of Petri-net 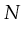
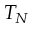 the transitions of Petri-net
the transitions of Petri-net 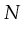
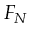 the flow relation of Petri-net
the flow relation of Petri-net 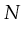
-
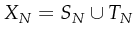 as the union of places and transitions of
Petri-net
as the union of places and transitions of
Petri-net  .
.
An elementary Petri-net is a 4-tuple
![]() whereby
whereby ![]() describes the underlying Petri-net and
describes the underlying Petri-net and ![]() defines the marking (which
tokens are where).
defines the marking (which
tokens are where). ![]() is the initial marking, or the startup
tokens of the Petri-net. To define the transition from one Marking
to another (or from one elementary Petri-net to another elementary
Petri-net) we need to define pre- and post-conditions of a single
transition:
is the initial marking, or the startup
tokens of the Petri-net. To define the transition from one Marking
to another (or from one elementary Petri-net to another elementary
Petri-net) we need to define pre- and post-conditions of a single
transition:
Informally, the above definition states that the precondition of ![]() is the set of all elements, either places or transitions, which have
a link toward
is the set of all elements, either places or transitions, which have
a link toward ![]() . The postcondition of
. The postcondition of ![]() is the set of all places
or transitions that have an outgoing link toward
is the set of all places
or transitions that have an outgoing link toward ![]() . We can easily
extend this pre-, post-condition definition of a transition to a
set of transitions.
. We can easily
extend this pre-, post-condition definition of a transition to a
set of transitions.
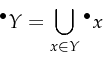
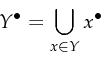
A transition ![]() is enabled, given marking
is enabled, given marking ![]() if and only
if all preconditions of
if and only
if all preconditions of ![]() hold for
hold for ![]() and no postcondition of
and no postcondition of
![]() holds for
holds for ![]() . We will write this down formally as:
. We will write this down formally as:
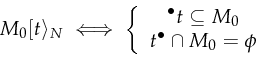
The notation
![]() can be read as: transition
can be read as: transition ![]() from Petri-net
from Petri-net ![]() is enabled under marking
is enabled under marking ![]() .
.
When an enabled transition is executed the precondition of the transition is removed from the marking and the postcondition of the transition is added to the marking. We write this down as
This notation can be read as: under marking ![]() the transition
the transition
![]() of Petri-net
of Petri-net ![]() give rise to marking
give rise to marking ![]()
A marking does not often gives rise to another uniquely defined marking. Depending on the executed transition other markings could be the result. Formally,
This can be read as: Given marking ![]() and Petri-net
and Petri-net ![]() , then
, then
![]() contains all the possible markings after one
transition.
contains all the possible markings after one
transition.
Some properties of elementary Petri-nets are:
- Every place can contain at most one token. No duplicates are allowed.
- Tokens represent boolean values: true or false, no content can be passed from one place to another
- Given a certain transition, the time necessary to check the preconditions
and post-conditions is known:
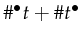 .
This is a nice property since it allows us to execute an elementary
Petri-net at a fixed rate.
.
This is a nice property since it allows us to execute an elementary
Petri-net at a fixed rate.
11 Formal Definition of CPNets
We will now define Colored Petri-nets formally. The definition given below is, to a large extent, based on the well known work of [Jen94]. However, other and often older definitions exists such as referenced in [EK98].
Before we can explain the nitty gritty detail of colored Petri-nets we need the ability to describe multiple tokens at the same place. Since this is something that cannot be easily expressed with mathematical sets, one resorts to multi-sets:
A multi-set is a set in which every element can occur multiple
times. Formally a multi-set ![]() is defined over a certain underlying
set
is defined over a certain underlying
set ![]() as a function that maps every element of S to a natural number:
as a function that maps every element of S to a natural number:
![]() . The domain of the multi-set: the occurrence
counts of every possible element of
. The domain of the multi-set: the occurrence
counts of every possible element of ![]() are called the coefficients
of
are called the coefficients
of ![]() . All possible multi-sets associated with a certain set
. All possible multi-sets associated with a certain set ![]() will be denoted as
will be denoted as ![]() . This should not be compared
to the power-set, denoted
. This should not be compared
to the power-set, denoted ![]() which is the set of all possible
subsets.
which is the set of all possible
subsets.
A second preliminary before we can explain the formal side of colored
Petri-nets are expressions. The guards and actions work on
values. The way in which these are represented is currently left open,
any type of expression can be inserted into a colored Petri-net. For
example, one can use ![]() expressions, or simple algebraic expressions.
One can choose whatever fits best. Of course, certain formal analysis
will no longer be possible if one chooses a language too expressive.
On the other hand, since we are not interested in model checking at
this stage we can safely choose
expressions, or simple algebraic expressions.
One can choose whatever fits best. Of course, certain formal analysis
will no longer be possible if one chooses a language too expressive.
On the other hand, since we are not interested in model checking at
this stage we can safely choose ![]() -expressions. Once one has
chosen an expression language one cannot change this anymore within
the same Petri-net. In the following definitions we will refer to
an expression as
-expressions. Once one has
chosen an expression language one cannot change this anymore within
the same Petri-net. In the following definitions we will refer to
an expression as ![]() .
. ![]() (with a capital) refers to all possible
expressions. For every expression
(with a capital) refers to all possible
expressions. For every expression ![]() it should be possible
to obtain the type and free variables. We should also be able to evaluate
it under a certain binding of values to variables:
it should be possible
to obtain the type and free variables. We should also be able to evaluate
it under a certain binding of values to variables:
- A type is a set of possible values, e.g; a type can be something like
 or it can be something like
or it can be something like
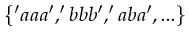 .
A type is not necessarily infinite. The boolean type:
.
A type is not necessarily infinite. The boolean type:
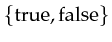 will be referenced to as 'bool'.
will be referenced to as 'bool'.
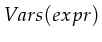 returns the set of unbound variables within
returns the set of unbound variables within 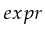 .
.
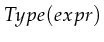 returns the set of possible values the expression can
return.
returns the set of possible values the expression can
return.
- A binding of a set variables
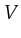 which associates with each element
which associates with each element
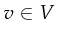 an element out of
an element out of 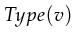 . So
. So
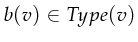
- The value of an expression
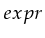 under a certain binding
under a certain binding 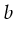 is
written down as
is
written down as
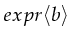 . The expression is evaluated
similarly to
. The expression is evaluated
similarly to 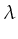 calculus by substituting every variable
calculus by substituting every variable
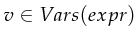 with the value
with the value 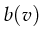 .
.
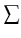 is a non empty set of types, called color sets.
is a non empty set of types, called color sets.
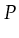 ,
, 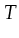 ,
, 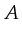 are, similarly to low level Petri-nets, the places,
transitions and the flow relation between places and
transitions.
are, similarly to low level Petri-nets, the places,
transitions and the flow relation between places and
transitions.
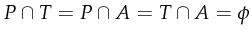 . The flow relation A
contains tuples from
. The flow relation A
contains tuples from
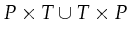 . This is in contrast
to the definition given in [Jen94], in which a node-function
is added to the Petri-net which maps an arc to such a tuple. This
little change however doesn't change any semantics associated with
the net as explained in [Jen94].
. This is in contrast
to the definition given in [Jen94], in which a node-function
is added to the Petri-net which maps an arc to such a tuple. This
little change however doesn't change any semantics associated with
the net as explained in [Jen94].
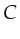 is a color function,
is a color function,
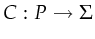 . This function associates
a type with every place. All tokens present at a place
. This function associates
a type with every place. All tokens present at a place 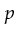 must be
of type
must be
of type 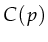 .
.
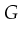 is a guard function,
is a guard function,
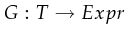 such that
such that
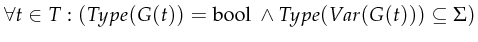 .
Informally speaking, we associate with every transition an expression
(the set of all expression is called
.
Informally speaking, we associate with every transition an expression
(the set of all expression is called 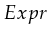 ). This expression should
result in a boolean type and all variables used within the expression
should be known, hence be part of
). This expression should
result in a boolean type and all variables used within the expression
should be known, hence be part of 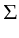 .
.
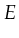 is an arc expression, or action:
is an arc expression, or action:
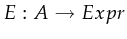 such
that
such
that
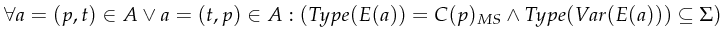 whereby
whereby 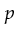 the place of
the place of 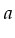 is. The arc expression associates with
every arc an expression, which will be used to verify or create new
token-values. Every arc expression should evaluate to a set of tokens
(a multi-set over the different types allowed by the place).
is. The arc expression associates with
every arc an expression, which will be used to verify or create new
token-values. Every arc expression should evaluate to a set of tokens
(a multi-set over the different types allowed by the place). 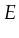 contains input expressions as well as outgoing actions.
contains input expressions as well as outgoing actions.
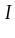 is an initialization function:
is an initialization function:
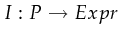 such that
such that
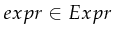 has no free variables and
has no free variables and
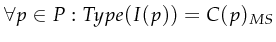
-
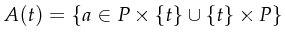 which returns the arcs
associated with the transition t.
which returns the arcs
associated with the transition t.
-
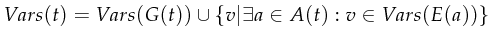
A marking is a multi-set over ![]() . The initial marking
. The initial marking ![]() is obtained from
is obtained from ![]() as follows
as follows
This means that there must exist a binding satisfying the guard (![]() )
and all expressions placed on the incoming arcs result in something
of the correct type. When an enabled transition
)
and all expressions placed on the incoming arcs result in something
of the correct type. When an enabled transition ![]() is executed the
marking
is executed the
marking ![]() changes to
changes to ![]() as follows :
as follows :
12 Tractability Overview
- [co-NP] A problem
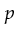 is co-NP if
is co-NP if 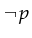 is NP. co-NP
problems often seem harder than NP problems, however it is still
an open question whether co-NP = NP.
is NP. co-NP
problems often seem harder than NP problems, however it is still
an open question whether co-NP = NP.
- [EXPTIME] A problem of size
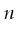 is EXPTIME if there is a constant
is EXPTIME if there is a constant
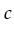 and the time to solve the problem takes at most
and the time to solve the problem takes at most 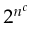 .
.
- [EXPTIME-complete] A problem is EXPTIME-complete if it is in EXPTIME
and other problems within EXPTIME are reducible to it. Essentially
this declares a class of problems which can be solved within exponential
time. It is known that EXPTIME
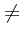 PTIME.
PTIME.
- [Non-deterministic] A machine is non-deterministic if it may execute different branches parallel on the same input.
- [NP] A problem is NP if it can be solved in polynomial time by a nondeterministic machine.
- [NP-complete] A problem is NP-complete if other NP-complete problems can be reduced to it.
- [P] A problem of size
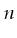 is P if there is a constant
is P if there is a constant 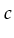 and
the time to solve the problem is at most
and
the time to solve the problem is at most 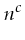 .
.
- [P-complete] A problem is P-complete if it is in P and other problems are reducible to it.
- [P-hard] A problem is P-hard if itself is not necessarily in P but other P-problems may reduce to it.
13 Summary: Advantages of using Petri-nets
Petri-nets have a number of very appealing properties. For an in-depth discussion of all these properties of Petri-nets, see [KCJ98].
- They are specified by means of a graphical representation. A representation that is intuitive and covers in one drawing enough detail to understand what the represented model is about.
- Petri-nets have a description of both states and actions, this in contrast to state diagrams or transition diagrams, which cover only part of the behavior of a system.
- Colored Petri-nets even include data manipulation within the Petri-net. A colored Petri-net covers state transition, state of a system and data manipulation in one drawing.
- Petri-nets are a formalism that can describe a system at any level of abstraction. Petri-nets can be used to describe the interaction between high level modules as well as the full interaction within these modules. Petri-nets can be described to specify a large variety of different systems. This can be illustrated by pointing out the number of practical situations in which Petri-nets have helped.
- The basic building blocks of Petri-nets are places, transitions (and tokens for colored Petri-nets). These primitives are easy to understand and very powerful.
- Petri-nets allows modularization of systems by means of hierarchical decomposition. Petri-nets can be combined using certain operators, which we will not discuss here. See [BFF+95] for more information.
- For real time systems, Petri-nets can be extended with a time concept. [PM93,BMAPY97]
- Petri-nets are stable toward minor changes of the modeled system. This is proved by many practical experiences. It means that small modifications of the modeled system does not require a complete rewrite of the Petri-net. In many other description languages this is not the case (e.g.: finite automaton).
- Petri-nets have a large number of formal analysis, by which properties of the modeled system can be verified. This includes: construction of occurrence graphs (which global states are reachable), calculation of invariants (pre- and post- conditions checking), reductions (shrink down a Petri-net but still preserve a number of properties) and checking of structural properties (such as starvation).
Bibliography
- BFF+95
-
Eike Best, Hans Fleischack, Wojciech Fraczak, Richard P. Hopkins, Hanna
Klaudel, and Elisabeth Pelz.
A Class of Composable High Level Petri Nets with an Application to the Semantics of .
.
In Giorgia De Michelis and Michel Diaz, editors, Application and Theory of Petri Nets, volume 935 of Lecture Notes in Computer Science, pages 103-120. Springer Verlag, 1995.
Describes a set of high level operations to compose petri-nets. - BMAPY97
-
Marius Bozga, Oded Maler, Amir Pnueli, and Sergio Yovine.
Some Progress in the Symbolic Verification of Timed Automata.
In O. Grumberg, editor, Proc. 9th International Conference on Computer Aided Verification (CAV'97), volume 1254, pages 179-190. Springer Verlag, 1997.
Describes how BDD (Binary Decission Diagrams) can be used in certain domains for a faster timing verification of large Petri Nets. - BP96
-
Eike Best and Ctuscia Palamidessi.
Linear Constraint Systems as High-Level Nets.
In Ugo Montanari and Vladimiro Sassone, editors, CONCUR, volume 1119, pages 498-513. Springer Verlag, 1996.
Makes the mapping from linear programming to timed Petri-nets. Also proves that constructing a reachability graph of timed Petri-Nets is NP-complete. - EK98
-
Mohammed Elkoutbi and Rudolf K. Keller.
Modelling Interactive Systems with Hierarchical Coloured Petri Nets.
Proceedings of the Conference on High Performance Computing, April 6-9 Boston 1998.
Given a set of UML usage scenarios, a Petri-net is generated. - EN94
-
Javier Esparza and M. Nielsen.
Decidability Issues for Petri Nets.
In Bulletin of the EATCS, volume 52, pages 115-129, February 1994.
A good introduction to the decidability issues of Petri-nets. - ERV96
-
Javier Esparza, Stefan Romer, and Walter Vogler.
An Improvement of McMillan's Unfolding Algorithm.
In Int'l Proceedings of Tools and Algorithms for Construction and Analysis of Systems, volume 1055 of Lecture Notes in Computer Science, pages 87-106. Springer Verlag, 1996.
Explains the reason behind Petri-net unfolding, their limitations and improves McMillans original algorithm. - Jen94
-
K. Jensen.
An Introduction to the Theoretical Aspects of Coloured Petri Nets.
In J.W. de Bakker, W.P. de Roever, and G. Rozenberg, editors, A Decade of Concurrency, volume 803 of Lecture Notes In Computer Science, pages 230-272. Springer Verlag, 1994.
Very good introduction to coloured petri nets. A must read for everyone involved with petri-nets. Also covers formal analysis of Petri Nets. - Jør
-
Jens Bæk Jørgensen.
Construction of Occurrence Graphs with Permutation Symmetries Aided by the Backtrack Method.
Technical report, Computer Science Department, University of Aarhus, Ny Munkegade, Bldg. 540, DK-8000 Aarhus C, Denmark.
Explains how to detect self-symmetries during reachability analysis by means of backtracking. However, not a published paper, it is a very interesting read. - KCJ98
-
Lars M. Kristensen, Soren Christensen, and Kurt Jensen.
The Practitioner's Guide to Coloured Petri-nets.
International Journal on Software Tools for Technology Transfer, pages 98-132, 1998.
This paper provides a comprehensive road map to the practical use of CPNets and the Design/CPN tool. The paper is self-contained and does not assume any prior knowledge of Petri nets. - LLPY97
-
K. Larsen, F. Larson, P. Pettersson, and W. Yi.
Efficient Verification of Real-Time Systems: Compact Data Structure and State-Space Reduction.
In Presented at 18th IEEE Real-Time Systems Symposium. San Francisca, California, USA, pages 14-24, December 1997.
Tries to solve the memory-requirements of reachability checks of timed automata. - Moo96
-
Simon W. Moore.
Data-flow machines.
University of Cambridge, http://www.cl.cam.ac.uk/users/swm11/dataflowlecture/dataflowlecture.html #compare, 25 April 1996.
Historically interesting pages. It is surprising to see how the evolution of dataflow machines follows closely the evolution of Petri nets. - Pet81
-
James L. Peterson.
Petri Net Theory and the Modeling of Systems.
Prentice-Hall, Englewood Cliffs, New Jersey, April 1981.
Chapter 7 describes how a number of extensions to Petri-nets break certain decidability issues. - PM93
-
P.Altenbernd and R. Milczewski.
Description of Timing Problems Using Petri Nets for Level-Independent Timing Verification.
Int'l Proceeding ACM/SIGDA Workshop on Timing Issues in the Specification and Synthesis of Digital Systems (TAU), August 1993.
Describes a number of complementary techniques to verify the dynamic and static aspects of timed petri nets. - Rei00
-
W. Reisig.
An Informal Introduction To Petri Nets.
Proc. 21st Int'l Conf on Application and Theory of Petri Nets, Aarhus, Denmark, Humboldt University of Berlin, June 26-30 2000.
Although a difficult read, it's a good introduction to the formal aspects of elementary Petri-nets. - SJ75
-
G. J. Sussman and G. L. Steele Jr.
Scheme, an Interpreter for Extended Lambda Calculus.
December 1975.
The original paper that introduces Scheme. The paper itself is written on a good old fashioned typewriter, and some nostalgy can be found between the lines. A must read.
Footnotes
- ...1
- Instead of testing all transitions to a certain marking it would be more useful to check only all postconditions of a marking.
- ... conservative2
- A Petri-net is said to be conservative if the total amount of tokens present doesn't change over time.
| http://werner.yellowcouch.org/ werner@yellowcouch.org |  |