| Home | Papers | Reports | Projects | Code Fragments | Dissertations | Presentations | Posters | Proposals | Lectures given | Course notes |
|
|
An experiment in automatic Adaptor Generation by means of Genetic Algorithms / Aamas2002Werner Van Belle1* - werner@yellowcouch.org, werner.van.belle@gmail.com Abstract : Mobile multi agent systems can be seen as a basis for global peer to peer computing. Nevertheless such an open environment makes it difficult to write agents which can interface with other agents because it is an excellent area for interface conflicts. Conflicting interfaces can be remedied by using adaptors. It is possible to automatically generate those glue-adaptors by means of genetically engineered classifier systems, which use Petri-nets as a model for the underlying interfaces. This paper reports on an experiment that illustrates this approach.
Keywords:
classifier systems petri-nets asynchronous communication open distributed systems adaptor generation interface conflicts |
Table Of Contents
Introduction
Mobile multi agent systems are a good basis for global peer to peer computing. In such a world, agents communicate with each other to reach specific goals. Applications are defined by the interactions of multiple agents which usually are written by different developers and different organisations. Over time, this results in interface conflicts, which makes it difficult to create applications which keeps working without a lot of reintegration.
In comparison to standard desktop software this is nothing new, only, when working with agents, the scale of the problem differs. In standard software development we deploy a certain application using a number of components and whenever new components come up, we reintegrate our application and release a new version. With software agents this is not possible because 1) we don't necessarily know with which agents our agents will communicate when executing on the net and 2) agent implementations can change over time without prior notification, thereby altering the offered API in a syntactic or semantic way. Whenever this happens, agents using this 'altered' API, will not work anymore. This will typically result in a cascaded application breakdown.
As long as we don't solve the problem of interface differentiation in some automatic fashion, mobile multi agent systems, with their very dynamic nature, may just be too impractical for programmers to use.
Genetic algorithms can provides us with a mean to automatically create program code for those adaptors and solve a number of interface conflicts automatically.
This paper reports on an experiment we performed to create automatic interface adaptors between agents. First we will explain what view we use on mobile multi agent systems, next we explain what kind of (typical) interface conflict we use in our experiment. Then we explain what a typical genetic algorithm looks like, which leads us to section 5 where we discuss the used model. Section 6, 7 then shows how this works on our previously introduced case.
Mobile Multi Agent Systems
Regarding the terminology mobile multi agent system there is some confusion. A multi agent system in AI [1] denotes a software system that simulates the behaviour of large groups of interacting agents (called multi agents), without focusing on the distribution aspect of these systems. In the world of distributed computing, a mobile multi agent system is a distributed environment in which multi agents can execute [2]. We adopt the second definition. A mobile multi agent is an active autonomous software component that is able to communicate with other agents; the term mobile refers to the fact that an agent can migrate to other agent systems, thereby carrying its program code and data along with itself.
A requirement for automatic adaptor generation is that we should be able to place at runtime adaptors between two agents in a completely transparent way. This can only be done if a number of requirements are met:
- Implicit Addressing: No agent can use an explicit address of another agent. This means no IP-number, DNS-name or alike can be used by agents. So we need to work in a connection oriented way. The connections are set up solely by one agent: the connection broker. The connection broker will also place adaptors where necessary. Jini [3] can be seen as a good example of this approach.
- Disciplined Communication: No agent can communicate with other agents by other means than the ports. An agent should not open a socket himself, or use files on disk to communicate with other agents. All communication should pass through the ports.
- No Shared Memory: All messages passed over a connection should be copied. Messages cannot be shared by agents (even if they are on the same host), because this would result in concurrency problems.
So, our mobile multi agents can be compared to processes [4, 5, 6]. Agents can communicate with each other only by sending messages over a communication channel [7]. An agent can have multiple communication channels: one for every communication partner, or more than one for every interface on a communication partner. Communication channels are offered by means of ports on the agent. In our system, agents communicate asynchronously and always copy their messages completely upon sending (see figure 1). This, because synchronous communication can be easily expressed with asynchronous constructs, while the opposite is difficult.
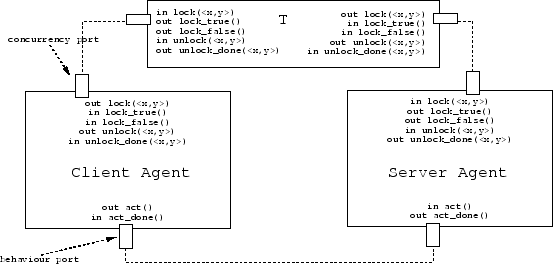 Figure 1: Client and server agent, both honouring the
same interface, whereby the client agent sends out
lock requests and the server agent can accept incoming
lock requests. Agents interact with each other over ports. This enables us to easily place
adaptors in between them. (Eg: Adaptor T)
Figure 1: Client and server agent, both honouring the
same interface, whereby the client agent sends out
lock requests and the server agent can accept incoming
lock requests. Agents interact with each other over ports. This enables us to easily place
adaptors in between them. (Eg: Adaptor T)
|
The connections between agents are full duplex. This means that every agent can send and receive messages over a port. This brings us in a situation where a certain interface is required from another agent and where an agent can provide a certain interface. E.g: an agent can accept incoming 'lock' requests and send back a result. In this case the agent provides a locking interface. If an agent requires a locking interface it will send out a lock and wait for an incoming result.
The above view on agents with the given requirements are no restraint. In fact, most mobile multi agent systems use these requirements because they are inherent distributed systems and typically distributed systems are bound by such a constraints.
The Case
The case we will use in our experiment is a typical problem of open distributed systems: how agents synchronise with each other. In closed distributed systems this is not really a problem. A server provides a concurrency interface (typically a transaction interface) [8] which can be used by clients. The clients have to adhere to this specification or they won't work. Since the server concurrency API doesn't change that much this is a usable setup.
In peer to peer computing, every agent has to offer a concurrency interface, and has to use the concurrency interfaces provided by other agents. To which extent an agent provides a concurrency interface is often a problem. It can provide a full-fledged optimal transaction interface or it can provide a simple lock/unlock interface. How two interfaces of a different kind interface with each other gives rise to problems.
In our example we use a simple lock/unlock interface of the server which a client can typically use to lock a resource and then use it. This API is as follows:
port concurrency
incoming lock(resource)
outgoing lock_true(resource)
outgoing lock_false(resource)
// lock_true and lock_false are sent back whenever a lock
// request comes in: lock_true when the resource is locked,
// lock_false when the resource couldn't be locked.
incoming unlock(resource)
outgoing unlock_done(resource)
// will unlock the resource. Send unlock_done back when done.
In our case, the server agent also offers some behaviour on another port. This behaviour is as simple as possible.
port behaviour
incoming act(resource)
outgoing act_done(resource)
// will perform some action on the agent.
Even with this simple definition of a concurrency interface, the semantics can be implemented in different ways. We will use two kinds of concurrency implementations:
Counting Semaphores
In our first version, somebody can lock a resource multiple times. Every time the resource is locked the lock counter is increased. If the resource is unlocked the lock counter is decreased. The resource is finally unlocked when this counter reaches zero. These semantics allows us to use routines which autonomously lock resources.
Binary Semaphores
The second version of our locking semantics, doesn't offer a counter. It simply remembers who has locked a resource and doesn't allow a second lock. When unlocked, the resource is fully unlocked.
Differences in how the API considers lock and unlock can give rise to interface conflicts. In figure 2 the client agent expects a counting semaphore from the server agent. The server agent offers binary semaphore. The client can lock a resource twice and expects that the resource can be unlocked twice. In practice the server just has marked the resource as locked. If the client now unlocks the resource, the resource will be unlocked. Acting upon the server now is impossible, while the client expects it to be possible.
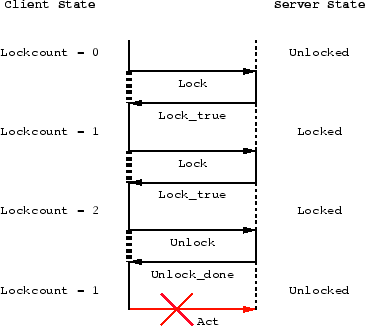 Figure 2: An
interface conflict when the client agent expects a counting semaphore
from the server agent and the server agent only offers a binary
semaphore.
Figure 2: An
interface conflict when the client agent expects a counting semaphore
from the server agent and the server agent only offers a binary
semaphore.
|
In the remaining of the paper we will try to generate an adaptor agent between both locking strategies automatically. This will be achieved by means of genetic algorithms, which are introduced in the next section.
Genetic Algorithms
A genetic algorithm [9] is an algorithm which tries to solve a problem by trying out a number of possible solutions. Every solution is measured with respect to the problem at hand. From the best solutions, new solutions are created. This process is repeated until a suitable solution is found. The solutions to a problem are called chromosomes or individuals. Every individual has a number of parameters which can be modified. This are the genes. A generation is a set of individuals which all try to solve the same problem(s). How well an individual performs is called the fitness of the individual.
When a generation is measured we keep (reproduce) 10% of the best individuals. We throw away 10% of the worst individuals (not fit enough) and add crossovers from the 10% best group. A crossover is a random selection of genes from each individual. The other 80% are simply mutated, which means that the genes of each individual are simply changed at random. The control flow of a typical genetic algorithm can be seen in figure 3.
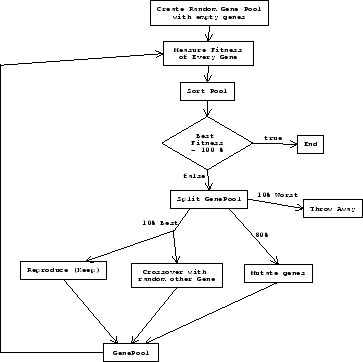 Overview of a genetic algorithm
Overview of a genetic algorithm
|
- What are the individuals ?
What are the genes of the individuals (ie, the parameters that can change for every individual) ? - How do we represent the individuals ?
- How do we measure the fitness of an individual ?
- How do we initially create individuals ?
- How do we mutate individuals ?
- How do we cross over individuals ?
In our case the individuals are the adaptor agents that we will place between communication partners. Representing the programs we place in an adaptor can be done in a number of different ways: we can use Scheme [10], Java [3] or other human-used languages as a representation. The problem with this is that human-usable languages are very verbose and the space of valid programs is very small. If we would generate a random program, there is 99% chance it won't even be syntactically correct. Therefore we choose another (well known) format for our programs: classifier systems. These will be explained in section
6.A problem of genetic algorithms, and learning systems in general, is that they cannot learn what they do not see. How can we make sure that our adaptors/individuals have enough input from the environment to make correct decisions ? This will be discussed in the next section.
Petri-nets
How can we make sure that our concurrency adaptors have enough input from the environment ? Our concurrency adaptors should at least know
- which state the client agent expects the server to be in. (or the projected client-state).
- in which state the server agent is.
Representing the state and state-transitions of an agent will be done by means of Petri-nets [11]. Petri-nets offer a model in which we can have multiple actors which each go from state to state by means of state transitions. Both concepts, the states as well as the state transitions, are modelled.
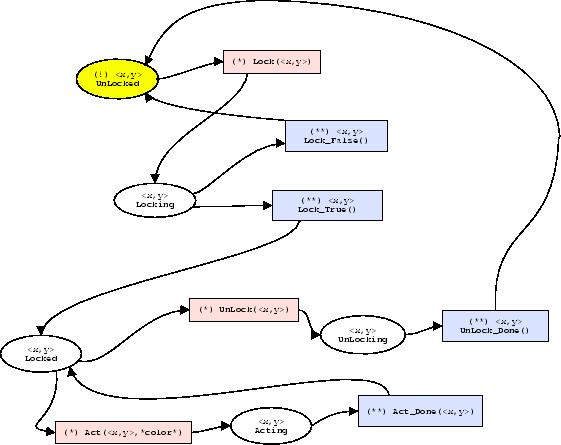 Figure:semaphore locking strategy,
described in a Petri-net. The red boxes (marked with *) are the
messages which either comes in are goes out. The blue ones (marked
with **) are exactly the opposite.
Figure:semaphore locking strategy,
described in a Petri-net. The red boxes (marked with *) are the
messages which either comes in are goes out. The blue ones (marked
with **) are exactly the opposite.
|
For example, in figure 4 one sees how a binary semaphore locking strategy is modelled. States are shown as circles, while transitions are shown as boxes. The current state unlocked is coloured in yellow (marked with a '!'). From this state the agent requiring this interface, can choose only one action: lock. When it chooses this action, it is in the locking state until lock_true or lock_false comes back. Note that we can also use this Petri-net to model the behaviour of an agent which provides this interface. It is perfectly possible to offer an interface which adheres to this specification, in which case, the incoming lock is initiated from the client, and lock_true or lock_false is sent back to the client when making the transition.
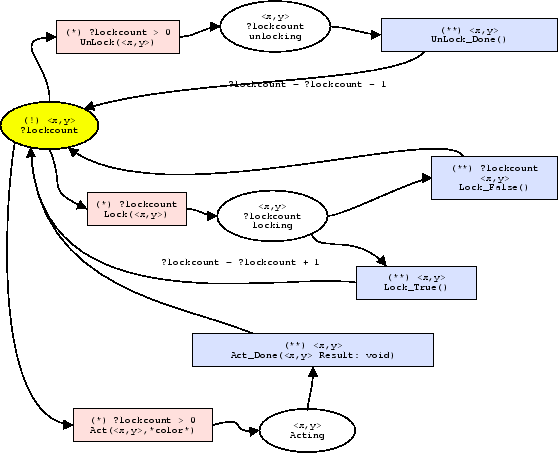 Figure 5:Counting semaphore locking Strategy described as a Petri-net.
Figure 5:Counting semaphore locking Strategy described as a Petri-net.
|
Figure 5 represents the counting semaphore locking strategy. One sees how a transition can only be made when a certain condition holds true: an agent can only unlock when it has a lock count which is larger than 0. The agent state holds this extra field: ?lockcount.
In the next section we will discuss the representation we will use for our adaptors (the individuals in the genetic algorithm). To be able to make correct decisions this representation needs enough input from its environment. In our experiment we use the petri-net states as input for our adaptors.
Classifier Systems
Adaptors should ease the semantic differences between two agents. Since we want to learn this we need to specify our programs in some kind of way. We choose to use classifier systems for this because it is simple, contains a memory and is Turing complete.
A classifier system [12] is a system which has an input interface, a classifier-list and an output interface. The input and output interface put and get messages to and from the classifier-list. The classifier list takes a message list as input and produces a new message list as output. Every message in the message list is a set of bits (0 or 1) which are matched against a set of classifiers. A classifier, also called a classifier rule, contains a number of (possible negated) conditions and an action. We will work with four conditions.
Conditions and actions are both ternary strings which can contain 0, 1 or #. A '#'-character is a pass-through which, in a condition, means 'either 0 or 1 matches'. If found in an action, we simply replace that character with the character from the original message (see figure 6).
 Figure 6: Illustration of how actions produce
a result when the condition matches. ~ is negation
of the next condition. In this illustrative example only two conditions
are used.
Figure 6: Illustration of how actions produce
a result when the condition matches. ~ is negation
of the next condition. In this illustrative example only two conditions
are used.
|
Such a classifier system will need to reason about the actions to be performed based on the available input. The input of a classifier system consists of a full description of the client state, a full description of the server state and possible the requested actions from either the client or the server. To be able to distinguish all those different kinds of messages we reserve the 3 first bits in every message for internal use (shown in figure 9). After the first 3 bits comes either some domain dependent description of the state (of client or server), or a domain dependent description of the action which should be taken.
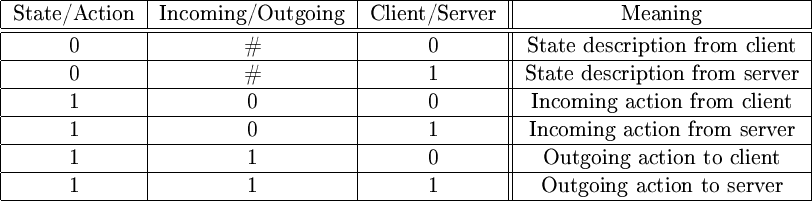 Figure 7: The first 3 bits of a classifier message describes what kind of message it is.
Figure 7: The first 3 bits of a classifier message describes what kind of message it is.
|
If we consider for example actions coming from the client, it would contain the name of the message and the position. The possible actions sent to the client are return of different function calls. On server side, the outgoing actions are returns from function calls and the incoming actions are the calls which can be executed upon the server. Figure 8 illustrates this.
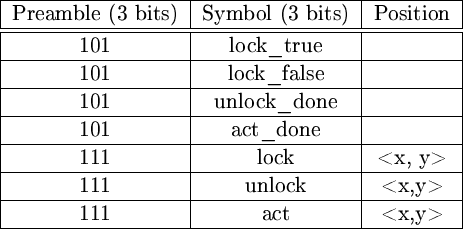 Figure 8: Possible client and server actions. Please
note that the symbols are bit- encoded in practice.
Figure 8: Possible client and server actions. Please
note that the symbols are bit- encoded in practice.
|
The representation of the Petri-net state offered by both agents will us the semantics described in figure 9. We model the full state representation one classifier message. We define the semantics of our messages as a 14 bit tuple (shown in figure 9), where the first 7 bits are the possible server actions, the next 7 bits represent the possible client actions. In our example we do not model the petrinet states of client of server, but only the petri-net transitions, because it reduces the complexity and expresses the same.
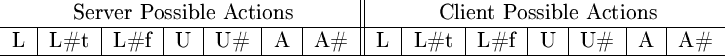 Figure 9:
L = lock; L#t = lock_true; L#f = lock_false;
U = unlock; U# = unlock_done; A = act; A# = act_done. A bit is
set when either a certain action is possible or a certain action is
required.
Figure 9:
L = lock; L#t = lock_true; L#f = lock_false;
U = unlock; U# = unlock_done; A = act; A# = act_done. A bit is
set when either a certain action is possible or a certain action is
required.
|
With these semantics for the messages, simply translating a request from the client to the server requires 1 rule. Another rule is need to translate requests from the server to the client (see figure 10).
 Figure 10: Blind translation between client
and server agents. Column condition 2 to 4 are omitted because they are not neceassary.
Figure 10: Blind translation between client
and server agents. Column condition 2 to 4 are omitted because they are not neceassary.
|
Although this is a simple example, more difficult actions can be represented. Suppose we are in a situation where the client uses a nested-locking strategy and the server uses a non-nested locking strategy. In such a situation we don't want to send out the lock-request to the server if there is a lock count is larger than zero. Figure 11 shows how we can represent such a behaviour.
 Figure 11:Translating a client-lock to a server lock when necessary.
Figure 11:Translating a client-lock to a server lock when necessary.
|
Adaptor Generation
As seen in section 4 a genetic algorithm requires individuals to test. We defined our individuals as classifier systems. They form the chromosomes of the genetic algorithm while the classifier conditions and actions are the genes. This method of using full classifier systems is also known as the Pittsburgh approach.
Individuals are initially empty. Every time a certain situation arises and there is no matching gene we will add a new gene. This gene, which is a classifier rule has a matching condition with a random action on the server and/or the client from the list of possible actions. This guarantees that we don't start with completely useless rules which cover situations which will never exist and allows us to generate smaller genes which can be checked faster.
Mutating individuals is done by randomly adapting a number of genes. A gene is adapted by selecting a new random action.
To create a crossover of individuals we iterate over both classifier-lists and each time we decide whether we keep the rule or throw it away.
Fitness is measured by means of a number of test-sets (which will be discussed in the next section). Every test-set illustrates a typical behaviour (scenario) the client will request from the server. The fitness of an individual is determined by how far the scenario can execute without unexpected behaviour. Of course this is not enough, we should not have solutions which completely avoid the server. For example, return lock_true every time a request comes in from the client, without even contacting the server. To avoid this kind of behaviour from our algorithm the test-set will need a covert channel over which it can contact the server to verify some things.
The Experiment
Setup
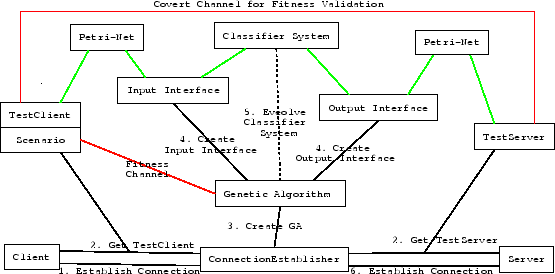 Figure 12:The setup of the system.
Figure 12:The setup of the system.
|
The experiment (pictured in 12) is set up as a connection broker between two components. The first component tries to make contact with the server by means of the broker. Before the broker sets up the connection it will generate an adaptor between the two parties to mediate slight semantic differences. It does this by requesting a test-agent from both parties. The client will produce a test-client and a test-scenario. The server will produce a test-server. In comparison with the original agent, these testing agents have an extra testing port, over which we can reset them. Furthermore, this testing port is also used as the covert channel for validating actions at the server.
The genetic algorithm, using a gene pool of 100 agents, will now use the test-agents to measure the fitness of a particular classifier system. Only when a perfect solution is reached; ie a correct adaptor has been found, the connection is set up.
Scenarios
The scenarios offered by the client are the ones which will determine what kind of classifier system is generated. We have tried this with three scenarios. Scenario 1 is a sequence: [lock(), act(), unlock()] x 3. (See figure 13) Scenario 2 is basically the same: [lock(), act(), act(), unlock()] x 3. The reason why we added such a second look-alike scenario will become clear in our observations. The third scenario is the case we explained earlier in the paper.
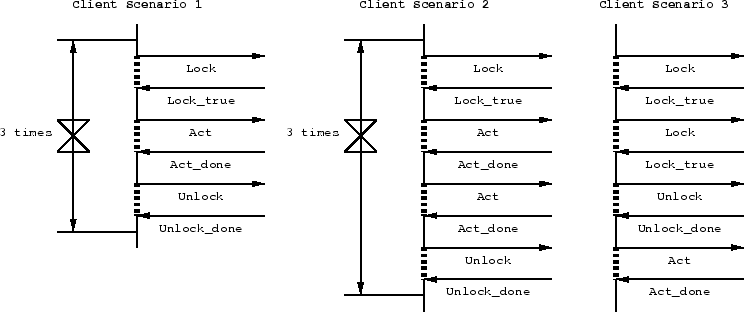 Figure 13:The three test scenarios we used to measure the
fitness of an adaptor. The dashed vertical lines are waits for a specific
message (Eg: Lock_true).
Figure 13:The three test scenarios we used to measure the
fitness of an adaptor. The dashed vertical lines are waits for a specific
message (Eg: Lock_true).
|
Observations
Without the covert channel
If we don't use the covert channel to check the actions at the server side, the genetic algorithm often creates a classifier which doesn't even communicate with the server. In such a situation the classifier would immediately respond lock_true whenever the client requests a lock.
With covert channel, only scenario 1
If we use the covert channel to measure the fitness more accurately, we see that a perfect solution is created within approximately 11 generations. In this case the fitness of each individual was measured by scenario 1 and scenario 3. See figure 14.
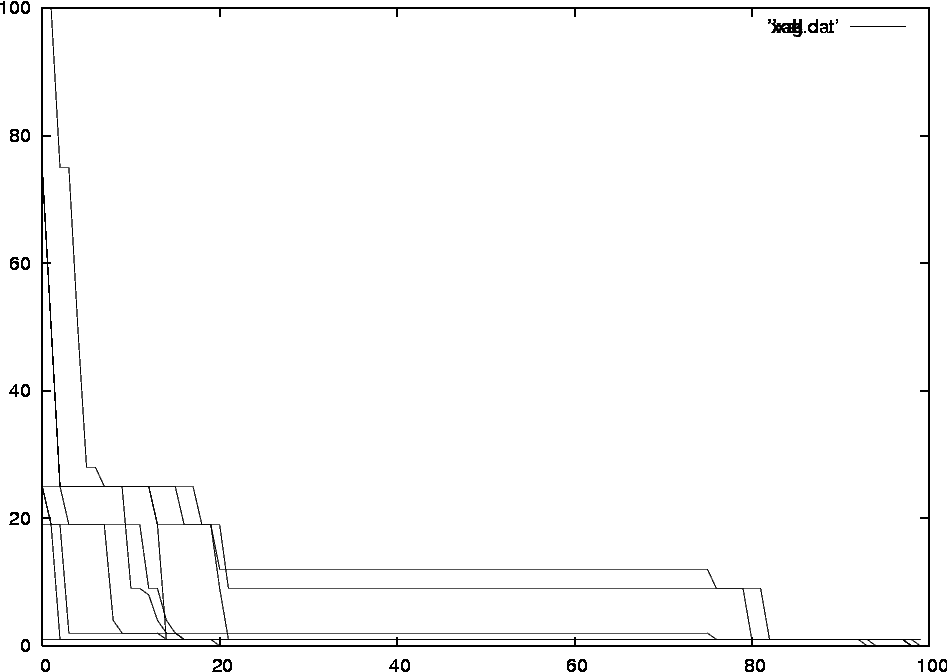 Figure 14:Fitness of the individuals in each generation
Figure 14:Fitness of the individuals in each generation
|
Anticipation of what will happen
One of the learned classifiers developed a strange behaviour. Its fitness was 100%, but it worked asynchronously, as illustrated in figure 15. At the moment an act request arrived from the client it sent this message to the server, which would respond with act_done. In response to this act_done the adaptor would automatically send back an unlock operation to the server. The server would respond with unlock_done, to which the classifier would send an act_done to the client. The client in its turn now send a lock_request which immediately results in an unlock_done from the classifier.
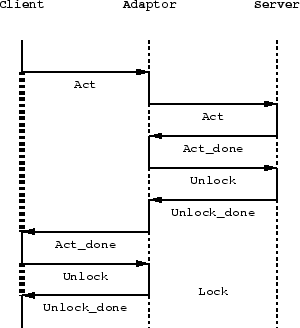 Figure 15:How an adaptor anticipates the next request
from the client and afterwards fakes a correct response.
Figure 15:How an adaptor anticipates the next request
from the client and afterwards fakes a correct response.
|
This example shows how such a learned algorithm can anticipate future behaviour.
Too much anticipation of what will happen
A problem we encountered was the fact that sometimes, the adaptor anticipates too much and after the first act, doesn't stop acting anymore. We solved this problem by assigning a fitness of zero to such solutions.
Fitness measured with scenario1 and scenario2 and scenario3
If we measure the fitness with both scenarios, we avoid a lot of the (wanted or unwanted) anticipated behaviour. After maximum 10 generations we find a perfect solution.
Conclusion & Future Work
In this paper we gave an overview of how we can create intelligent interfaces which can be used in open distributed systems.
Our approach lets a genetic algorithm learn a classifier system. This classifier system contains classifiers which react upon the context they receive from client and server. The context is defined as a combination of the possible client-side and server-side states.
The case studied was concurrency because this is known to be a major problem in peer to peer computing. It is clear that this approach is not restricted to the domain of concurrency.
As for future work there remains some important problems. First of all we need to do more rigorous experiments. This includes, using larger interfaces (with more functions, or larger petri-nets), using Turing complete classifier-systems and see how they evolve.
A second problem involves the use of the test-scenarios. The test scenarios should cover all the actions which will be invoked upon the server in all possible combinations. How can we write good tests which doesn't leave any open holes for the programmer. And if we can, are the petri-nets still necessary ? In other words: can we learn the model automatically just by looking at the interaction between the agents. The reason we used petri-nets is because they offer immediately a set of possible actions for each state. This reduces the time needed to learn an adaptor because it reduces the search space drastically. Of course these are not necessary, if we know the state we should now enough
A third problem is the representational mapping. In our example we use two alike representations. This makes learning an adaptor easy. To make this algorithm stronger we need a representational mapping which is able to translate one state to another state.
Acknowledgements
I would like to thank my promotor Theo D'Hondt for the discussions we had on this subject and for giving me the time to investigate this matter. Thanks to Johan Fabry, Tom Tourwe and Tom Mens for proofreading this paper.
Bibliography
| 1. | A real-life experiment in creating an agent marketplace. A. Chavez, D. Dreilinger, R. Guttman, Pattie Maes Proceedings of the Second International Conference on the Practical Application of Intelligent Agents and Multi-Agent Technology, April 1997. |
| 2. | Experiences in Mobile Computing: The CBorg Mobile Multi-Agent System Werner Van Belle, Johan Fabry, Theo D'Hondt, Karsten Verelst Proceedings TOOLSEE 2001, Zurich; IEEE Computer Society Press; pages: 1-9; volume: 38; address: http://borg.rave.org/; editor: Wolfgang Pree; March; 2001 http://werner.yellowcouch.org/Papers/expmobcom/index.html |
| 3. | Core Jini W. K. Edwards. The Sun Microsystems Press Java Series. Prentice Hall, 1999 |
| 4. | A Calculus of Mobile Processes, Part I + II R. Milner, J. Parrow, D. Walker Information and Computation; volume: 100; number: 1; pages: 1-77; 1992 |
| 5. | Communicating and Mobile Systems: the Pi-calculus Robin Milner Cambridge University Press; May; 1999 |
| 6. | The Polyadic pi-Calculus: A Tutorial Robin Milner LFCS report ECS-LFCS-91-180 |
| 7. | The Component System Werner Van Belle, David Urting institution: Technical Report 3.4 for the {SEESCOA} project, Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussel, Belgium; October 2000, http://www.cs.kuleuven.ac.be/cwis/research/distrinet/projects/SEESCOA |
| 8. | Concurrent programming in Java. Design principles and Patterns Doug Lea 2nd Edition, ISBN: 0-201-31009-0, The Java Series, Addison Wesley, 2000 http://g.oswego.edu/ |
| 9. | Genetic Programming; on the programming of computers by means of natural selection. J. R. Koza. MIT Press 1992 |
| 10. | Scheme: an Interpreter for Extended Lambda Calculus Gerald Jay Sussman, Guy L. Steele Jr. Mass. Institute of Technology, Artificial Intelligence Laboratory, Cambridge; December; 1975 |
| 11. | An Informal Introduction To Petri Nets. W. Reisig. Proc. Int'l Conf. Application and Theory of Petri Nets, Aarhus, Denmark, June 2000. |
| 12. | Introduction to evolutionary computation. R. Poli Technical report, School of Computer Science; University Of Birmingham, October 1996. |
| http://werner.yellowcouch.org/ werner@yellowcouch.org |  |