| Home | Papers | Reports | Projects | Code Fragments | Dissertations | Presentations | Posters | Proposals | Lectures given | Course notes |
|
|
Ambient Actors as a Formalism for Ubiquitous and Mobile ComputingWerner Van Belle1*+ - werner@yellowcouch.org, werner.van.belle@gmail.com Abstract : Networks formed by the interconnection of mobile wireless devices are often called mobile ad-hoc networks. Such networks are highly volatile because communication partners can move in and out of range. This leads to unwanted interruptions of communication sessions, which in turn complicates the development of software that relies on a long term distributed state. Standard solutions seem inadequate because all too often they assume an inherent client server role or they assume a bound latency on communication sessions. One cannot make such assumptions in mobile ad-hoc networks. In order to resolve this matter a programming model must support the ability to pick up previous communication sessions; it must remember the devices/resources it has seen in the past; and it must provide a realistic approach towards concurrency, taking into account the limitations of a peer to peer ad-hoc network. This article presents the ambient actor model which extends the operational semantics of the actor model to capture the limitations posed by this novel paradigm
Keywords:
ambient pervasive ubiquitous computing asynchronous distributed systems actor systems |
Table Of Contents
1. Motivation
Networks formed by the interconnection of mobile wireless devices are often called mobile ad-hoc networks. Such networks are highly volatile because communication partners can move in and out of range. This leads to unwanted interruptions of communication sessions, which in turn complicates the development of software that relies on a long term distributed state. Standard solutions seem inadequate because all too often they assume an inherent client server role or they assume a bound latency on communication sessions. One cannot make such assumptions in mobile ad-hoc networks.
In order to resolve this matter a programming model must support the ability to pick up previous communication sessions; it must remember the devices/resources it has seen in the past; and it must provide a realistic approach towards concurrency, taking into account the limitations of a peer to peer ad-hoc network.
This article presents the ambient actor model which extends the operational semantics of the actor model to capture the limitations posed by this novel paradigm.
Pervasive computing captures the idea that computing technology will gracefully integrate into our everyday life such that the user is no longer aware of the technology [1]. From a hardware point of view much progress has been made the past couple of years. Technology such as WiFi, Bluetooth [2] and 802.11 [3] provide already decent hardware abstractions and improvements in chip design already led to the creation of ultra-low power chips that organize themselves automatically into time synchronized ad-hoc networks [4, 5, 6]. Research into such sensory networks concerns itself with the question on how to aggregate information properly. This can be useful to acquire and query sensory information from different locations, such as in vibration monitoring of buildings [7].
Such highly visible and interesting applications provide a radical rework of the software layer [8] but provide little help for more common 'personal digital assistant' (PDA) applications. As a working example in this article, we consider a PDA, that travels along with its user. As the user moves about, the software on the PDA encounters new environments, each possibly containing new devices to provide useful information and resources (e.g: other PDA's, printers, local computers and so on). We find that this kind of applications tend to rely heavily on abstraction layers that might not be feasible to realize because they assume inherent client-server roles, stable connections and/or availability of specific communication partners.
Based on such scenarios, we determined a number of novel concepts for, and restrictions on, the communication architecture for mobile ad-hoc networked devices.
- Local communication
- In pervasive computing, the single most outstanding concept is probably 'location'. Whether we work with ad-hoc sensor networks or PDA's, such devices are mobile and in order to allow to software to react and recognize its environment, the communication architecture needs to link every computation to a physical location. Furthermore, unlike most desktop computers today, mobile devices are not necessarily continuously connected to a network such as the Internet. Local direct device-to-device communication might be the only means for devices to communicate with other devices in their immediate proximity.
- Connection Volatility
- The limited communication range of the wireless technology combined with the fact that users can move out of range can result in broken connections at any point in time. Therefore, communicating devices that perform a meaningful task together cannot assume a stable connection. However, upon re-establishing a broken connection, users typically expect the task to resume and performed, regardless of the quality and availability of connections.
- Finding Resources
- If a user moves about with his/her mobile device, remote resources become dynamically available or unavailable. This is in contrast with stationary networks in which references to remote resources are obtained based on the explicit knowledge of the availability of the resource. A challenge in mobile ad-hoc networks is how to recognize particular resources and services [9]. The problem of unreliable availability of communication partners connections can also be present in open distributed systems, such as Internet, but they are less prominent, because the incidence rate of unavailable communication partners is much lower and communication partners are often unavailable for only small amounts of time.
- Autonomy
- Most distributed applications today are developed using the client-server approach. The server often plays the role of a ``higher authority'' which coordinates interactions between the clients. In mobile networks a connection to such a ``higher authority'' is not always available. Every device should be able to act as an autonomous computing unit. This means that no device should indefinitely postpone its own processing when waiting for information from other devices.
Currently none of the formalisms we studied was able to capture those four basic premises into a coherent formal model. Therefore, we felt the need to take these basic facts and incorporate them into a formalism for ubiquitous computing, which is sometimes also called 'ambient intelligent computing' [10].
2. Related Work & Comparative Analysis
Based on the concepts identified in the previous section, we now analyse the state of the art of programming models for ubiquitous computing systems. The presented formalisms were mainly conceived in the context of peer to peer networks, open distributed systems or mobile multi agent research. Table 1 presents the overview of our findings. For every model we investigated whether the model a) provides the concept of locations, b) whether communication can only occur within the same locations. We were also interested in c) whether the model supports the detection of incoming or outgoing communication candidates and will notify the program layer. d) The 'resource' column describes whether remote resources can be detected using some form of resource descriptor (e.g: pattern-matching on capabilities). Finally, we probed the autonomy of every model by looking at the synchronicity of the model (The reason for this will become clear in section 3.1
| Only Local | Detection of incoming | Finding of | Asynchronous | |
| Name | Communication | and leaving devices | Resources | Communication |
| Linda | No | No | No, possible | No |
| Locality Based Linda | No | No | No, possible | No |
| Mobile Ambient Calculus | Yes | No | No, possible | No |
| Distributed Join Calculus | No | Extension | Yes | No |
| No | Half | No | No | |
| ActorSpaces | No | No | Yes | Yes |
| Actor systems | No | No | No | Yes |
| Ambient Actors | Yes | Yes | Yes | Yes |
2.1. Tuple Spaces: Linda & Locality Based Linda
Linda [11, 12] is a coordination language based on Tuple spaces. There are several primitives that make communication explicit in the code. There is a primitive for putting values in the Tuple space (asynchronous) and primitives for getting values from the Tuple space (blocking). Tuple spaces are interesting because they allow communication without the need to specify the communication address of the receiver (which is also known as anonymous communication). If used properly, such a Tuple space might be usable for local communication. Nevertheless, the standard Linda architecture is based on a central server architecture, with one central Tuple space in which to put tuples. This makes it not suitable for ad-hoc wireless network environments.Locality based Linda [13] is an extension to Linda but with the explicit notion of locations. Primitives in Locality based Linda now work on a specific Tuple space. Anonymous communication becomes impossible, because the location needs to be provided. In our context this would mean that the addresses of communicating devices need to be known, which is impossible to determine in ad-hoc wireless network environments. The model also does not define what happens with communications when the target location is unavailable or unreachable.
- Local communication: Standard Tuple-spaces rely on a centralized architecture, which does not provide a concept for the locality of an agent. Extensions exist that take into account locality (e.g: locality based Linda), but in these communication remains global by prefixing every Tuple with a target Tuple space.
- Detection of incoming and leaving devices: Tuple spaces do not provide a standardized way to detect incoming or outgoing devices since there is no concept of direct communication between the devices (all communication goes through the global Tuple space).
- Finding Resources: Tuple spaces can be used to detect specific resources, based on some form of pattern matching, however, there is no standard provision that dictates how resources are to be found and to what kind of messages a resource/device needs to reply. On the other hand, standard Tuple space provide for anonymous communication which is already an important concept to realize automated resource finding. Therefore, we marked 'finding resources' as 'No, but possible'.
- Autonomy: Tuple spaces provide asynchronous events, however these are often wrapped in blocking primitives which makes the models not suitable for networks with unbound latencies.
2.2. Mobile Ambient Calculus
The mobile ambient calculus [14] expresses an abstraction between mobile computing and mobile computation in administrative domains. Mobile computation is the physical movement of devices between administrative domains, while mobile computing is the movement of a logical process (also called migration). The mobile ambient calculus describes movement of processes between different locations and communication between Ambients that are located in an ambient. Mobile Ambients allow the posting of anonymous messages (without explicitly targeting the receiver). This is a concept that can be used for detection of resources since a mobile ambient can post its own information. Notwithstanding, the model itself does not provide a standardisation how such a mechanism needs to work.- Locations and local communication: The mobile ambient calculus provides the concept of 'ambient' to represent locations and location awareness. It also assumes that only local communication between Ambients in the same environment is possible.
- Detection of incoming and outgoing Ambients and notification to the program is not provided by the mobile ambient calculus.
- Finding resources: The mobile ambient calculus provides anonymous communication, which might be used to set up some form of resource recognition. Notwithstanding, there is no standard provided.
- Autonomy: The mobile ambient calculus relies on distributed computation, in which parts of the computation can be redirected elsewhere. This means that any device can receive new incoming Ambients. We perceive this as problematic because device might leave indefinitely and thus delete part of the computational trace. Furthermore, typical communications are written in a blocking manner.
2.3. Distributed Join Calculus
The distributed join calculus [15] gives semantics for logical movement (migration), failures and failure detection of agents. The distributed join calculus comes with a number of possible extension, among which locality as defined in the mobile ambient calculus and failure detection.- Local communication is not available in the standard model, instead it assumes a fully interconnected network.
- Connection Volatility: Detection of incoming and outgoing devices can be realized as an extension to the system.
- Finding Resources seem standard in the Distributed Join Calculus.
- Autonomy: Blocking primitives are standard in this formalism and thus is not reconcilable with the autonomy of devices.
2.4. The 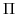 -calculus
-calculus
The - Local communication: The
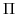 -calculus has no concept of locality and thus there is also no
assumption that only local communication is possible.
-calculus has no concept of locality and thus there is also no
assumption that only local communication is possible. - Connection Volatility: processes in this model communicate through channels. Those channels, comparable to TCP connections, might allow for the detection of leaving devices. There is no standard support to notify the presence of new processes.
- Finding Resources: The
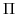 -calculus does not provide a means to recognize and anonymously detect
new resources.
-calculus does not provide a means to recognize and anonymously detect
new resources.
- Autonomy: Similar to the observations on the mobile ambient calculus: the migration of channels and processes does not respect the autonomy of the receiving device and the standard use of blocking primitives does not work well in networks with unbound latencies.
2.5. Actors
The actor model was developed by Hewitt [18] in the late seventies and later further developed by Agha [19, 20]. It was only in the late nineties that Agha et. al published a description of the operational semantics [21] of an actor system. Since the ambient actor model we will present, bases itself on the standard actor model, we will elaborate on some of its details. This will provide the reader with a better understanding of what lies at the heart of actors.
The Actor programming language [22]was designed for use in open distributed network environments (i.e. the Internet). A distributed application is modelled with actors that are distributed throughout the network. Communication between actors occurs solely with asynchronous message passing. Figure 1 shows the conceptual representation of an actor. Each actor has a behavior associated with it, which defines how it handles incoming messages. Incoming messages are handled by the actor its own thread of control. An actor is fully encapsulated and can only be addressed by other actors through its mailbox. In other words if an actor sends a message to another actor or itself it always places a message in this mailbox. A message is transparently and non-deterministically selected from the mailbox and processed according to the actor its behavior. Fairness is assumed such that all messages are eventually processed.
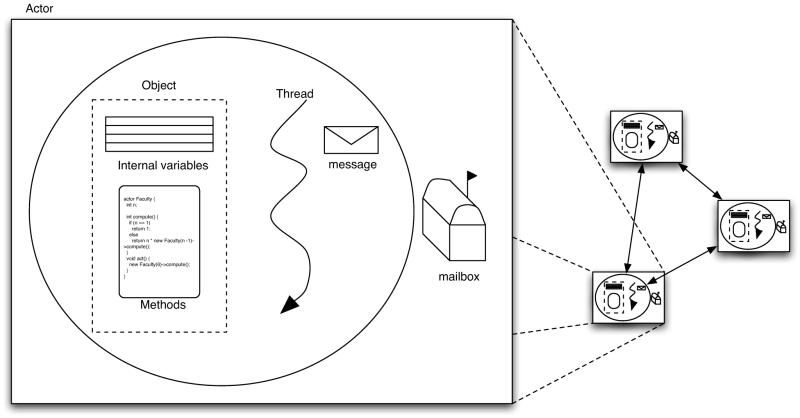
|
The semantics of the actor programming language [21] are defined as an extension of the operational semantics of a simple functional language. The behavior of an actor is modelled using functions, each taking one parameter, which is a message. Based on this parameter a number of expressions can be evaluated. In the operational semantics of the actor language the functional language is conceptualized by the untyped lambda calculus [23, 24] which is further extended with three actor primitives to support programming in a distributed environment:
- New actors can be created using the letactor primitive. The letactor primitive takes one argument, a function that is the initial behavior of that actor and returns the mail address of an actor.
- Messages are sent to known actors using the send primitive. The send primitive takes two arguments, the recipient's actor address and a message. Such a message can contain the address of other actors.
- An actor can modify its own behavior using the become primitive. The become primitive takes one argument, a function that is the new behavior of the actor. There is no shared data between actors.
These primitives are illustrated by the example shown below, which is an implementation of an ML reference cell expressed in the actor language defined by the operational semantics. This cell example also illustrates how the become operator can be used to model state.
if(get?(m),
seq(become(b(c)), send(cust(m), c)),
if(set?(m),
become(b(contents(m))),
become(b(c)))))
In the ![]() -calculus functions are first-class entities and do
not necessarily have a name. Such anonymous functions are of the form
-calculus functions are first-class entities and do
not necessarily have a name. Such anonymous functions are of the form
![]() where a is an argument and exp is
the body of the function. The last expression that is evaluated
determines the return-value of the function. In the
where a is an argument and exp is
the body of the function. The last expression that is evaluated
determines the return-value of the function. In the
![]() -calculus functions take only
one argument at a time.
Multiple arguments are simulated by currying. This is the process
where one function returns another function that takes one argument
and this process is repeated for all arguments.
-calculus functions take only
one argument at a time.
Multiple arguments are simulated by currying. This is the process
where one function returns another function that takes one argument
and this process is repeated for all arguments.
The function ![]() describes the behavior of a
cell actor. The
function call to rec calculates the fixed-point of a function
[25] and calls the
describes the behavior of a
cell actor. The
function call to rec calculates the fixed-point of a function
[25] and calls the ![]() -expression with that
fixed-point as its argument. Hence,
-expression with that
fixed-point as its argument. Hence, ![]() refers to a function
which takes two arguments c and m as its arguments
and where b has been bound to the fixed point in the lexical
environment of that function. The argument c refers to the
contents of the cell and the variable m refers to the message
that an actor receives.
refers to a function
which takes two arguments c and m as its arguments
and where b has been bound to the fixed point in the lexical
environment of that function. The argument c refers to the
contents of the cell and the variable m refers to the message
that an actor receives.
The cell-behavior responds to two kinds of messages, get- and set-messages. The get-messages are responded to in two steps: first, the become operation is used to define the replacement behavior of the actor. The replacement behavior is defined with a recursive call through the fixed-point and the contents of the cell remains unchanged. Hence, the replacement behavior of the actor will refer to a function that takes one argument m that has b bound to the fix-point and c bound to the original contents of the cell. Next, the contents of the cell is sent to the customer of the message. The set-messages are responded to by changing the function to a new one with the variable c bound to the contents found in the message m.
In the code that handles the get-message, we find that a become is placed before a send instruction. This order of statement influences the degree of concurrency. Once the become operation has been performed the actor can process its next message while the expressions that follow the become are executed concurrently. The become operation dynamically creates a new anonymous (An anonymous actor is an actor whose address is not known by any other actor in the system). actor which executes the following expressions, in this case the send, while the current actor processes its next message in the context of its new behavior. Accordingly the actor model supports intra-object concurrency. What is more, this intra-object concurrency does not lead to race conditions on the internal state of an actor. The main reason for this is that the state change (achieved by installing another function using the become operation) of an actor occurs in a single operation, because naturally the functional language does not include assignments. Hence, only a become can change the state of an actor.
The function which describes the behaviour of the cell can now be used to initialize the actor:
The actor language relies on an actor system to support parallelism and communication between actors. An actor system hosts multiple actors. These actors may concurrently process messages from one another, irrespective of their individual states. Conceptually, an actor system can be modelled as a message set and the behavior of the actors running on the system. This message set contains two types of messages: 1) messages received, but not yet processed and 2) messages sent, but not yet transmitted. Both types are discussed below:
- A message, whose target address is that of an actor running in the actor system, is taken from the message set and passed as an argument to the function that is assigned to the target actor address. When the message set is empty the system waits for a new message to arrive. As explained above, an actor can handle the next message from the moment it has performed the become operation.
- When a message is sent then the message is put in the message set. When the target actor address of the message is that of an actor running on another actor system then the message is transparently transferred to the message set of that actor system. The operational semantics of the actor language do not define any order in which the messages from the message set are processed, but it assumes fairness so that no starvation can occur.
We now discuss the applicability of actor systems in light of mobile ad-hoc networks.
- Local Communication: The actor model was designed for open distributed networks, where communication partners are sometimes unavailable for a short period of time. The model guarantees delivery through the use of message sets: messages sent to actors running on an unavailable actor system are kept in the message set until the actor system becomes available again for communication. Each actor system has its own message set that contains the messages sent, but not yet transmitted to another actor system and the messages received, but not yet processed. An actor system is therefore self-sufficient and does not rely on a general server infrastructure from the environment for its communication. The abstraction of an actor system however does not fit well with the concept of a location since every single device will need to run their own actor system. Actor systems rely on a virtual full interconnected network, without taking into consideration the mobility of devices nor the restriction that only local communication might be possible.
- Connection Volatility: A message set enables transparent asynchronous communication in intermittently connected environments, because a message is transparently and automatically transferred from the message set of the sender to the message set of the receiver whenever communication is possible. Hence, the connection between two actor systems is automatically restored after it was broken. This is important because it permits transparent communication in networks where failures are common, whereas many other asynchronous protocols put the burden of expressing delivery guarantees on the developer.
- Autonomy: The actor model explicitly states that no expressions containing closures can be communicated. Agha et al. [21] argue that this is not a serious limitation, because the actor address can be communicated instead and by sending messages to this actor address one can indirectly access the lambda-abstraction. We agree with this view and point out that, in order to remain autonomous, an actor cannot assume that incoming code will behave properly, and thus must treat transmitted data differently from other code. Furthermore, in the actor model, communication amongst actors can only occur by means of the send primitive. Compared to other distributed frameworks, no implicit communication is allowed through shared data. The send operation is also non-blocking and thus preserves the autonomy of a mobile device.
- Finding Resources: Finding and detecting new resources with the standard actor model seems complicated. In the actor model all resources that can be shared are modeled as actors and actors are referred to by actor addresses. Actors can only communicate with one another if they have an actor mail address. Miller et al. [26] noted that in capability secure languages, such as the actor model, actors can only make acquaintance with one another in four modes: connectivity by introduction (a message containing an actor address sent to another actor); connectivity by parenthood (when an actor creates another actor using letactor, then the creating actor has the address of the created actor); connectivity by endowment (an actor is initialized with the address of another actor); connectivity through system bootstrapping. This means that he actor model does not provide a means for an actor to independently get a reference to a remote actor in its direct environment. In other words, if two devices move in the communication range of one another then there is no rule that permits one actor running on a device to get a reference to another actor running elsewhere, unless they both have a reference to a third party acting as a middleman. Such a middleman could be a naming server or name registry which is used in middleware approaches, such as Java RMI [27] and CORBA [28, 29]. However, such a middleman would imply that infrastructure always needs to be present in the environment. This would not only conflict with the autonomy of mobile devices as explained in section 1 but the actor address of the software running on that infrastructure would need to be bootstrapped in all mobile devices. In other words: the standard actor model is unaware of the appearance and disappearance of other actors.
2.6. ActorSpaces
An extension of the actor model, named ActorSpaces, was proposed by Agha and Callsen [30] and defines how actors can be resolved in a distributed namespace. Distributed naming is a useful abstraction to address actors based on a specification rather than an explicit reference. The Actor-Space model extends the actor model with three new concepts:- Attributes: In the ActorSpace model, actors can be addressed by their actor address or by attributes. Attributes are patterns which provide an abstract specification of an actor. In contrast to an actor address, which is associated with exactly one actor, patterns can denote a group of actors; namely all actors that fulfill the abstract specification determined by the attributes.
- ActorSpaces: An ActorSpace is a computationally passive entity that determines the scope in which the pattern matching of attributes occurs.
- Capabilities: The security model is based on capabilities [31], which are unforgeable keys. Those keys can be created dynamically, compared and communicated over the network by actors. The correct capability is needed to change properties with respect to the distributed naming of an actor or ActorSpace.
Although the ActorSpace model introduces an interesting model to deal with the distributed naming problems of the actor model, there are a number of limitations that make the concepts impossible to use in the context of ad-hoc distributed systems. The problems originate from the fact that ad-hoc distributed systems typically involve network partitions (only small local communicating groups of devices). For example, suppose a number of actors are contained in an ActorSpace but some of these actors run on mobile devices that are currently not in the communication range. Hence, the ActorSpace is partitioned and it is undefined what happens when messages are sent to the actors in that ActorSpace. Also, it is unclear on which device the data structure that holds the configuration of the ActorSpace should be placed. When the node that maintains that data structure is not in the communication range at the moment a send or broadcast operation is performed, then the semantics is undefined. Another point where semantics of the operations of the ActorSpace model is not clear is when managers change the configuration of an ActorSpace in the face of such a network partition. Note that replication of the ActorSpaces data structure is not feasible, because an ActorSpace can be manipulated at runtime and keeping the replicas up-to-date and provide consistent access does not scale and leads to inconsistencies.
- Local communication: the ActorSpace model offers the idea of locations since it provides a range in which pattern searches occur. Communication is global and a full interconnect is assumed after the actor name has been resolved.
- Connection Volatility: incoming and outgoing devices are not detected and thus not notified towards the program.
- Finding Resources: The ActorSpace model provides an interesting mechanism to find and recognize resources within the local search environment.
- Autonomy: actors communicate asynchronously, resulting in non-blocking primitives.
3. The Ambient Actor Model
We find that none of the presented formalisms integrate the crucial concepts laid out earlier: a concept of locations; the restriction that only local communication might be possible; awareness of the local environment including notification towards the application when it changes; and a standardized mechanism to find anonymous resources and communication primitives that do not jeopardize the autonomy of a single actor.
In this section we introduce the ambient actor model, an extension of the operational semantics and the syntax of the standard actor model such that the few limitations of the actor model are resolved. We will refrain from giving all the definitions of the standard actor model, which can be found in [21]. We will however repeat definitions that we adapted to extend the operational semantics of the actor model or when they are essential to understanding the extensions.
The main addition to the actor model is the introduction of explicit mailboxes for each actor [32]. A number of mailboxes are used within the model to guarantee communication between local and remote actors. In a sense these are necessary to support the meta communication protocol between actors. The mailboxes are the standard inbox, which keeps track of incoming messages, the standard outbox, which keeps track of messages that should be delivered, the sent- and the rcvbox which keep track of, respectively, which messages have been sent and which messages have been processed by an actor. In this section we show that the introduction of these four first-class mailboxes addresses the reïfication of the communication traces, which was one of the missing criteria we identified in the original actor model. We will show that through the manipulation of these mailboxes actors are able to adapt their delivery strategy based on the needs of the application. What is more, actors can use the mailboxes to determine their communication state and as such implement customized schemes based on this state.
Aside from these mailboxes four other mailboxes are introduced to reïfy the environmental context of actors. Actors are usually interested the availability, appearance and disappearance of specific resources from the environment. For this reason, two mailboxes provided and required are added. These mailboxes contain the names of services that are provided to and required by an actor, respectively. These names of services determine what part of the environment is reïfied. The environment is reïfied through the introduction of the joined and disjoined mailboxes. These two mailboxes are transparently updated by the actor system and contain the actor addresses of resources that have appeared and disappeared. As such they reveal the environmental context to the actors.
3.1. Design
We briefly touch upon 4 design decision we made for the ambient actor model [33, 34].
- Isolated data-model
- Since programs running on different devices can be written in different programming languages we need a formal model that provides a well defined and language independent communication protocol. Such a communication protocol must allows actors to remain in full control of their execution state when receiving messages [35]. This means that one should not allow messages to be executed automatically or treated such that arbitrary code execution becomes possible. This effectively means that we are especially reluctant to include well know and widely adored features such as transmission of closures (allows for arbitrary code execution) and direct remote addressing (remote references to local objects). We believe that isolated data-models such as XML [36, 37] or KQML [38] or other form of graph or tree serialization are the proper way forward.
- Non-blocking communication
- Writing applications for volatile networks is difficult by means of synchronous communication (such as RPC [39]and RMI [40]). With synchronous communication there is a condition that the communication partner on the other end must be available. This condition does not hold anymore in a wireless network environment as communication partners are often not available and can become unavailable for communication at any point in time. Hence, existing synchronous communication models (such as the ones mentioned above) are not suitable for pervasive communication. With asynchronous (a.k.a. non-blocking) communication on the other hand there is no correlation between the sent-time and the receive-time of messages. This decouples the availability of communication partners in time and thus makes it appropriate in wireless network environments.
- Reïfied Message History
- Asynchronous communication comes with the cost that one must remember a previous communication state. Contrary to synchronous communication where such state is carefully managed on the runtime execution stack, the application program now needs to concern itself with session management. Such a message history kept by every individual partner effectively distributes the computational state such that all involved devices have only trace of the computation. In order to allow the application program to manage such a message history, we choose to reïfy it.
- Reïfied Environmental Context
- Mobility of devices implies changing environments, which further implies that the software needs to adapt to new environments. A formalism for mobile networks must thus provide a first class representation of the surrounding environment that is automatically updated as changes occur.
Despite the limitations of the actor model, it adheres to the non-blocking communication criterion and provides an isolated data model. Although the actor model does not completely support programming for mobile ad-hoc networks, we believe it provides a solid starting point to extend it such that the missing criteria, namely the reïfication of communication traces and environmental context, are supported too.
3.2. Extensions to Actors
The ambient actor model extends the call-by-value lambda in the same manner as the standard actor model introduces primitives such as send, become and letactor. However, dissimilar to the standard actor model, the letactor primitive has been decomposed into two primitives newadr and initbeh. The former creates a new actor address and the latter initializes the behavior linked to this actor address. Next to the standard actor primitives we added a number of primitives to manipulate mailboxes:- messages(e) returns the set of messages of mailbox e.
- add(mbxName, e) adds a message e to the mailbox with name mbxName. A message added to a mailbox that does not exist creates the mailbox.
- delete(mbxName, e) deletes a message e from the mailbox with name mbxName
3.3. Messages and Mailbox Associations
We now define a number of sets related to the representation of messages and mailboxes in the ambient actor model. We take as given countable sets
![]()
![]() where
where ![]() is all arity-n primitives.
is all arity-n primitives.
![]()
Say Y is a set then ![]() is the set of
finite
subsets of Y.
is the set of
finite
subsets of Y. ![]() is the set of
finite
multi-sets with elements in Y.
is the set of
finite
multi-sets with elements in Y. ![]() is the set of finite maps
from
is the set of finite maps
from ![]() to
to
![]() .
. ![]() be the domain of
be the domain of ![]() .
.
A message is
represented as a nested pair of value expressions, this
is in contrast with the message representation as defined in
[21] (where a
message was denoted with
![]() ). By representing the messages as a pair of values
the message becomes a first class value in the actor language. This
will prove useful to manipulate the mailboxes. Another difference
with the standard actor model is that the message includes the sending
actor (called the source). To make a clear distinction in the
definitions between messages and other pair values, we will identify a
pair that is used as a message with
). By representing the messages as a pair of values
the message becomes a first class value in the actor language. This
will prove useful to manipulate the mailboxes. Another difference
with the standard actor model is that the message includes the sending
actor (called the source). To make a clear distinction in the
definitions between messages and other pair values, we will identify a
pair that is used as a message with ![]() .
.
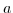 , the actor address of the source actor.
, the actor address of the source actor. 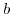 , the actor address of the target actor.
, the actor address of the target actor. 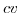 , a communicable value, constructed from atoms and actor addresses, but
not containing closures.
, a communicable value, constructed from atoms and actor addresses, but
not containing closures.
In the ambient actor model a message can be associated with multiple mailboxes. To denote these mailbox associations in the actor model we introduce the following set:
3.4. Actor Configurations
The operational semantics of the model itself is based on actor-configurations and reduction rules defined on these configurations. Conceptually, an actor configuration can be perceived as the runtime state of an actor system (discussed in section 2.5). Such an actor system runs on any computational device, such as a mobile phone or desktop.An actor configuration contains:
- the state of the actors in a configuration is given by an actor
map
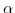 . Such an actor map is a finite map from actor addresses to actor
states. Each actor state is one of
. Such an actor map is a finite map from actor addresses to actor
states. Each actor state is one of
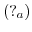 uninitialized
actor state created by an actor with address
uninitialized
actor state created by an actor with address 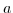
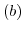 actor state
ready to accept a message where
actor state
ready to accept a message where 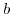 is
its behavior represented by a closure
is
its behavior represented by a closure ![$ [e]$](img57.png) actor in a
busy state executing expression
actor in a
busy state executing expression 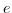 .
. 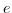 is either a value expression
or a reduction context R filled with a redex
is either a value expression
or a reduction context R filled with a redex 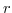 (written as
(written as ![$ {\tt R[}r{\tt ]}$](img60.png) ). The reduction context is used to describe internal transitions while
a message is being evaluated by the
). The reduction context is used to describe internal transitions while
a message is being evaluated by the 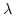 -function associated with the behavior. The current expression that is
evaluated is decomposed into a reduction context with a unique hole.
For the formal elaboration on reduction contexts we refer to the
standard actor model [21].
Suffice it to say that here that R in the following definitions ranges
over the reduction contexts. The redexes that are not actor-specific
expressions, namely the purely functional fragment of the language, are
inherited from the operational semantics of the standard actor model.
The redexes related to the actor operations are newadr(), init(
-function associated with the behavior. The current expression that is
evaluated is decomposed into a reduction context with a unique hole.
For the formal elaboration on reduction contexts we refer to the
standard actor model [21].
Suffice it to say that here that R in the following definitions ranges
over the reduction contexts. The redexes that are not actor-specific
expressions, namely the purely functional fragment of the language, are
inherited from the operational semantics of the standard actor model.
The redexes related to the actor operations are newadr(), init(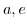 ), become(
), become(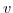 ), send(
), send(
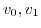 ), add(
), add(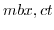 ), delete(
), delete(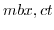 ) and messages(
) and messages(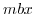 ).
).
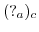 denotes an uninitialized actor
denotes an uninitialized actor 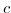 that was created by actor
that was created by actor 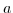 .
. 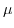 , a multi-set of mailbox associations.
, a multi-set of mailbox associations. 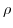 , receptionists, the actor addresses from this configuration that are
accessible from other actor configurations
, receptionists, the actor addresses from this configuration that are
accessible from other actor configurations 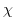 , external actors, the addresses of actors from other actor
configurations that can be accessed from this actor configuration.
, external actors, the addresses of actors from other actor
configurations that can be accessed from this actor configuration.
-
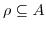 and
and 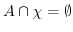 ,
, - if
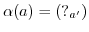 , then
, then 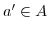 ,
,
- if
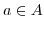 , then FV
, then FV
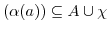 ,
,
- if
 , then
, then 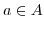
- if
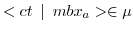 then FV
then FV
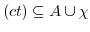
The fourth constraint is a new constraint and denotes that each mailbox in an actor configuration should be owned by an actor from the actor configuration.
3.5. Operational Semantics of Actor Configurations
Now that we have defined the necessary sets involved in the formalization of the operational semantics of the ambient actor model we can define the actual operational semantics. The operational semantics are defined as reduction rules on actor configurations. Conceptually, such a rule can be regarded as an evaluation step of an actor system. Each rule contains a labelAs in the paper of
Agha et al. [21] we
use the
following notation for maps: if the mapping ![]() and if
and if
![]() differs from
differs from ![]() in that
in that ![]() is omitted from its domain
then we write
is omitted from its domain
then we write ![]() as
as ![]() such that the focus is on
the state of actor
such that the focus is on
the state of actor ![]() . We follow the same convention for other maps
with actor addresses in their domain, such as mailbox associations.
. We follow the same convention for other maps
with actor addresses in their domain, such as mailbox associations.
In our model the
transitions (![]() ) are extended with an
environmental context set
) are extended with an
environmental context set ![]() . The set
. The set ![]() contains the
actor
configurations that are available (in the communication range of the
actor configuration on which the transition is defined) while the
reduction is performed. The introduction of this set is important to
reïfy the notion of environmental context in our extended model.
Below we explain and discuss the different rules.
contains the
actor
configurations that are available (in the communication range of the
actor configuration on which the transition is defined) while the
reduction is performed. The introduction of this set is important to
reïfy the notion of environmental context in our extended model.
Below we explain and discuss the different rules.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3.5.1. Basic Actor Operations
The first three reduction rules (- The
 rule above
delegates the purely functional expressions used in the actor program
to the functional redexes. The functional redex contains reduction
rules for function calls, cons-cell manipulation, branch-testing,
type-testing and equality. For the exact definition of these reduction
rules we refer the reader to [21].
rule above
delegates the purely functional expressions used in the actor program
to the functional redexes. The functional redex contains reduction
rules for function calls, cons-cell manipulation, branch-testing,
type-testing and equality. For the exact definition of these reduction
rules we refer the reader to [21].
- The semantics of the letactor primitive is formalized by two
rules,
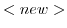 and
and 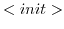 . The
. The 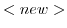 rule is used
to create a new actor with address a'. The
new actor is not initialized after this reduction. We say that a
variable is fresh with respect to a
context of use if it does not occur free or bound in any syntactic
entity. The new uninitialized actor is denoted with
rule is used
to create a new actor with address a'. The
new actor is not initialized after this reduction. We say that a
variable is fresh with respect to a
context of use if it does not occur free or bound in any syntactic
entity. The new uninitialized actor is denoted with 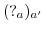 .
. - With the
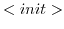 rule a new
actor is initialized with behavior
rule a new
actor is initialized with behavior 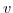 . Only the actor that created the actor a'
can initialize it.
. Only the actor that created the actor a'
can initialize it. - With the
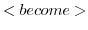 rule the actor can change its state and behavior, similar to the become
rule in the standard actor model. However, in the rule defined by Agha
et al. [21] the
expressions evaluated after a become will be further reduced in the
context of a new anonymous actor. It is this anonymous actor that
introduces the intra-object concurrency in the actor model.
rule the actor can change its state and behavior, similar to the become
rule in the standard actor model. However, in the rule defined by Agha
et al. [21] the
expressions evaluated after a become will be further reduced in the
context of a new anonymous actor. It is this anonymous actor that
introduces the intra-object concurrency in the actor model.
In the changes we have made, this remaining expression is not further reduced, changing its semantics similar to a break instruction found in many programming languages. The reason we removed intra-object concurrency is to ensure mailbox manipulations have correct semantics. Indeed, if the remaining expression is reduced in the context of an anonymous actor and mailboxes would be manipulated then the mailboxes of the anonymous actor would be manipulated instead of the actor that started to process the message. This would lead to awkward semantics. An alternative to this solution would be to let an anonymous actor manipulate the mailboxes of the actor that spawned it. However, this would introduce race conditions on the mailboxes. The topic of safe access to mailboxes is further discussed below in section 3.5.3.
3.5.2. Communication Rules
The remainder of the rules have been adapted to include the notion of mailboxes:- The
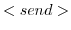 rule mildly
differs from the send rule found in the
actor model. The new rule reduces the send operation to placing the
message in the outbox of the actor in which the send operation is
reduced.
rule mildly
differs from the send rule found in the
actor model. The new rule reduces the send operation to placing the
message in the outbox of the actor in which the send operation is
reduced. 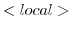 is a new rule
that was added to model local communication between actors. If the
message can be delivered locally (within the same actor configuration),
it is placed both in the target its inbox, and the sentbox of the
sender. The rule is defined such that communication can only occur when
the two actors involved in the communication are not in a busy state.
Similar conditions are also specified for the other i/o-transitions.
These conditions are necessary to preserve the model from race
conditions. This will be discussed in section 3.5.3.
is a new rule
that was added to model local communication between actors. If the
message can be delivered locally (within the same actor configuration),
it is placed both in the target its inbox, and the sentbox of the
sender. The rule is defined such that communication can only occur when
the two actors involved in the communication are not in a busy state.
Similar conditions are also specified for the other i/o-transitions.
These conditions are necessary to preserve the model from race
conditions. This will be discussed in section 3.5.3. 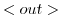 The out
reduction rule is used at the sending side for messages that cannot be
delivered locally, to transmit a message to another actor
configuration. Similar to the original model, the set of receptionists
is expanded with the local actor addresses that were communicated in
the message. The outgoing message is removed from the outbox.
The out
reduction rule is used at the sending side for messages that cannot be
delivered locally, to transmit a message to another actor
configuration. Similar to the original model, the set of receptionists
is expanded with the local actor addresses that were communicated in
the message. The outgoing message is removed from the outbox.
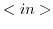 an actor
configuration receives a message from an external actor that runs on
another actor system. In this situation, the message is placed in the
inbox of the target actor.
an actor
configuration receives a message from an external actor that runs on
another actor system. In this situation, the message is placed in the
inbox of the target actor. 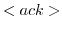 an actor
configuration receives an acknowledgment for a message it send and
places that message in the sentbox of the sending actor. This allows
the actor to verify which messages have actually been sent.
an actor
configuration receives an acknowledgment for a message it send and
places that message in the sentbox of the sending actor. This allows
the actor to verify which messages have actually been sent. 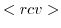 When a
message is available in the inbox of an actor, it can be received by
the actor and when it is processed by the actor, it is moved to the rcv mailbox. As a result, an actor has a history
of the messages that it processed. This proves to be useful for
determining the communication state of an actor as is shown in the
examples in section 4.
When a
message is available in the inbox of an actor, it can be received by
the actor and when it is processed by the actor, it is moved to the rcv mailbox. As a result, an actor has a history
of the messages that it processed. This proves to be useful for
determining the communication state of an actor as is shown in the
examples in section 4.
3.5.3. Mailbox Manipulation
![]() Some reduction rules have
been added to
manipulate and inspect the mailboxes from within the actor language.
With the
Some reduction rules have
been added to
manipulate and inspect the mailboxes from within the actor language.
With the ![]() rule one can access the content of a
mailbox.
The
rule one can access the content of a
mailbox.
The ![]() rule creates
a mailbox when it does not exist, if the
mailbox exists, the content will be added to the mailbox. The
rule creates
a mailbox when it does not exist, if the
mailbox exists, the content will be added to the mailbox. The ![]() rule delete a message from a
mailbox, when the last
message of a mailbox has been removed, the mailbox itself is removed.
The above reduction rules allow actors to manage mailboxes
explicitly. Note that there is no rule in which a message
automatically disappears from the system. This means that memory
management will have to be handled manually by the programmer. This
is because it depends on the semantics of the program whether a
message has become irrelevant to the program. For example, when a
certain task has completed and its associated messages are not
relevant anymore.
rule delete a message from a
mailbox, when the last
message of a mailbox has been removed, the mailbox itself is removed.
The above reduction rules allow actors to manage mailboxes
explicitly. Note that there is no rule in which a message
automatically disappears from the system. This means that memory
management will have to be handled manually by the programmer. This
is because it depends on the semantics of the program whether a
message has become irrelevant to the program. For example, when a
certain task has completed and its associated messages are not
relevant anymore.
When scrutinizing the ambient actor model, one has to investigate whether if there are concurrency issues involved with the reïfication of the mailboxes. For example, a possible race condition is an actor that deletes a message from its outbox at the moment it is transferred to the target actor its inbox. The operational semantics of the ambient actor model exhibit two mailbox properties that are important to avoid race conditions on the mailboxes of an actor.
- Mailbox Privacy
Each mailbox has a unique name within an actor. A mailbox is associated with exactly one actor and an actor cannot communicate a reference to one of its mailboxes. However, it is possible to communicate the name of a mailbox, but this name refers to the local mailbox of the receiving actor and not to the mailbox of the sending actor. Hence, mailboxes are never shared among multiple actors. - Serial Mailbox Access
In the ambient actor model a mailbox is manipulated by two different entities: the actor owning the mailbox and the actor system which updates mailboxes when communication events occur, for example when a message is transmitted. The operational semantics of the ambient actor model is defined in such a way that the manipulation of mailboxes by these two entities cannot occur concurrently. Indeed, the rules where the actor system manipulates mailboxes as a result of a communication event have the explicit condition that the actor whose mailboxes are being manipulated is not in a busy state. Hence, while an actor is processing a message its mailboxes can only be changed by itself, not by the actor system. Messages that the actor system cannot send at that time remain in the out mailboxes of the corresponding actors until they can be transmitted.
3.5.4. Handling Environmental Contexts
Applications running on mobile nodes need to have access to the reïfied environmental as discussed in the introduction, so that they can address local resources. The reïfication of the environmental context is supported with two reduction rules: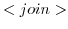 when two
actor configurations come in the communication range of one another
then every actor
when two
actor configurations come in the communication range of one another
then every actor 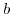 that requires
a certain pattern
that requires
a certain pattern 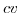 , which has become available in another actor configuration
, which has become available in another actor configuration 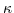 that is in communication
range, will be informed of this by receiving a ``join'' message in its
inbox. Also, for every matching pair of required-provided patterns, the
corresponding joined mailbox is updated. In the joined mailbox, a
special kind of message is stored, called a resolution. A resolution contains a) the pattern (
that is in communication
range, will be informed of this by receiving a ``join'' message in its
inbox. Also, for every matching pair of required-provided patterns, the
corresponding joined mailbox is updated. In the joined mailbox, a
special kind of message is stored, called a resolution. A resolution contains a) the pattern (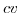 ) that has been matched and b) a provider actor
) that has been matched and b) a provider actor 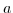 who provides the service represented by the pattern. Hence, the
resolutions found in the mailbox of an actor specify the actor
addresses of the resources that matched the pattern.
who provides the service represented by the pattern. Hence, the
resolutions found in the mailbox of an actor specify the actor
addresses of the resources that matched the pattern. - The
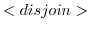 rule
specifies the semantics of two actor configurations that leave each
others communication range. Every actor that is aware of another joined
actor that has left the communication range, will be informed of the
disjoin. Once an actor is informed the corresponding resolution is
removed from the joined mailbox. Actors that have removed the matching
messages from their joined mailbox will not be informed.
rule
specifies the semantics of two actor configurations that leave each
others communication range. Every actor that is aware of another joined
actor that has left the communication range, will be informed of the
disjoin. Once an actor is informed the corresponding resolution is
removed from the joined mailbox. Actors that have removed the matching
messages from their joined mailbox will not be informed.
The join and disjoin operations are not the inverse of one another. After joining and disjoining two actor configurations, the state of the involved actor configurations is not necessarily the same as before the join operation. This is due to the fact that for every join or disjoin a number of messages are sent, which might influence the behavior of the involved actors.
4. Case Studies
Now that we have defined the operational semantics of the ambient actor model we show that it is useful in the context of mobile networks by means of two examples. The examples are defined with actor code based on the semantics of the ambient actor model from the previous section. The first example shows how anonymous communication can be expressed. In the second example we elaborate on a meeting scheduler application for use in a mobile ad-hoc network.In the examples below we use the convention that functions prefixed with mk create the respective messages and functions that end with a ``?'' are predicates. For example, mkPrint is a function that creates the print message and print? is a function that returns true if its argument is a print message.
4.1. Pattern-Based Communication
In section 3.1 we discuss that distributed naming is a good abstraction to communicate with resources in the environment for which the address is unknown. For example, an actor that wants to print a file on a printer first needs to locate a suitable printer in the environment and then communicate with it. With a distributed naming scheme both actions can be abstracted in a single communication instruction psend that allows an actor to be named based on its properties rather than on a specific address. Below is the definition of an actor using the psend abstraction to print a file from the moment it comes into communication range of an actor that provides a printing service.seq(psend('printer@300dpi, mkPrint(file)),
become(handleJoin))
In the ambient actor model the addresses of resources can be retrieved based on the pattern through the mailboxes that reïfy the environmental context. Hence, an actor can be described using a pattern that embeds the type information [41]or more semantic information about the service. We define a new communication primitive psend that takes two parameters: a service description pattern of the required actor and the message that is to be sent.
seq(add('required, pattern),
add('pending, msg))
The handleJoin definition listens for join messages that indicate that the joined mailbox has been changed. In such an event it runs through the resolutions in the joined mailbox. Each time a pattern that corresponds with the target of the messages in pending mailbox is found, the message is sent to the provider of the pattern and removed from the pending mailbox.
if(join?(msg),
for-each(
for-each(
if(eq?(target(pmsg), pattern(resolution)),
seq(send(provider(resolution), pmsg),
delete('pending, pmsg))),
messages('pending)),
messages('joined)))
This first example has shown that the ambient actor model contains the necessary primitives that can be used to build more complex distributed naming schemes. The distributed naming scheme is realized through an abstraction that unifies message sending with the discovery of services such that actors can send messages based on a pattern specification rather than their explicit mail address. This abstraction is implemented based on the mailboxes that reïfy the environmental context.
4.2. Meeting Scheduler
Suppose we have a calendar application (running on a mobile device such as a PDA or mobile phone) that helps us to schedule and remind us of appointments with a group of acquaintances. Each mobile device executes the agenda application and a request for a meeting can be initiated at any point in time, irrespective of whether the agenda applications of the acquaintances are available for communication. This kind of behavior is necessary to support the autonomous mobility of the users and the fact that some mobile devices may not be available due to volatile connections. For that reason, the application has to deal with volatile connections and the application may not rely on a central server architecture, which are two hardware phenomena we discussed in section 1. We assume that the mobile devices at some point in time will be in the communication range of one another.
The agenda application schedules a meeting in two steps.
- It tries to make a reservation in the agenda of the participants of the meeting.
- It confirms the reservation in the agenda of each participant if all individual reservations were successfully reserved.
4.2.1. Agenda Actor
Each agenda is initialized with the e-mail address of the agenda's owner. The e-mail address is combined with the type information of the application to form a pattern, which is returned by the mkPattern function, and uniquely identifies the agendas. This pattern is added to the provided mailbox such that the presence of each individual agenda of the participants can be detected.seq(add('provided, mkPattern(email)),
become(
For the sake of the argument, we have chosen to represent the agenda as a single slot that is available for meetings. The slot has three states: FreeSlot, ReservedSlot and ConfirmedSlot. A slot understands three messages, free, reserve and confirm and corresponding to the message it receives the slot moves into another state:
- free: when this message is received and the slot is in a reserved state then it becomes available for reservation. This message is used to undo a reservation.
- reserve: when the state of the slot is free and this message is received then the slot moves to the reserved state.
- confirm: when the state of the slot is reserved and a confirm message is received then the slot moves to the confirmed state.
if(free?(m),
become(b))
if(reserve?(m),
seq(send(sender(m), mkReserveAnswer(session(m), #true)),
become(
if(and(free?(m), eq?(id, session(m))),
become(
if(reserve?(m),
seq(send(sender(m), mkReserveAnswer(session(m), #false)),
become(b(id))))
if(and(confirm?(m), eq?(id, session(m))),
become(
if(reserve?(m),
seq(send(sender(m), mkReserveAnswer(session(m), #false)),
become(b(id)))))
Each reserved and confirmed state has a session id that is used to determine to whom the slot has been assigned. The slot only evolves into the corresponding state if the message contains the right session id.
4.2.2. Scheduler Actor
Each agenda application comes with a scheduler agent. This agent is responsible for contacting the agenda actors to schedule the meeting. In the actor definitions of the scheduler implementation below we use four helper functions:- a filter function that uses a predicate to filter elements in a
list (In the code below we use LISP [42, 24] terminology for our
function related to lists. A pair is created with the function cons.
The function car returns the first element of the pair, while the cdr
function returns the second element. A list of elements is represented
as a nesting of pairs. e.g. (1, 2, 3) is represented as (1, (2, (3,
'()))))
filter = rec(
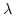 b.
b.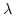 predicate.
predicate.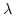 list.
list.
if(empty?(list),
emptyList,
if(predicate(car(list)),
cons(car(list), b(predicate, cdr(list))),
b(predicate, cdr(list)))))
- a map function that returns a transformed list and takes two parameters: a function that transforms elements and a list that is to be transformed is defined as in standard Scheme [42, 24] implementations [43].
- msend that allows sending a message to a list of actor addresses
or actors described with pattern descriptions (such as in the previous
example)
msend =
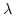 targets.
targets.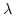 m.
m.
for-each(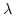 target.
target.
if(actorAddress?(target),
send(target, m),
psend(target, m)),
targets)
- madd that allows adding a list of messages to a mailbox
madd =
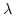 mbx.
mbx.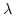 items.for-each(
items.for-each( item.add(mbx,item), items)
item.add(mbx,item), items)
- mdelete that allows to delete a list of messages from a mailbox
mdelete =
 mbx.
mbx. items.for-each(
items.for-each( item.delete(mbx,item), items)
item.delete(mbx,item), items)
The scheduling agent behavior is initialized as
![]() . The scheduler agent has an id that
is used to identify its session.
. The scheduler agent has an id that
is used to identify its session.
if(schedule?(m),
seq(msend(participants(m), mkReserve(id)),
become(
(id, participants(m), sender(m)))))
if(and(reserveAnswer?(m), eq?(id, session(m))),
if(success?(m),
if(eq?(map(sender,
filter(reserveAnswer?, messages('rcvbox)))),
participants),
seq(msend(participants,mkConfirm(id)),
become(
(id, participants, customer)))),
seq(msend(map(destination,
filter(reserve?, messages('sentbox)))),
mkFree(id)),
mdelete('outbox,
filter(reserve?, messages('outbox))),
send(customer, mkFailed()),
become(
seq(handleJoin(m),
become(b(id, participants, customer)))))
When handling a reserveAnswer message we make use of the mailboxes introduced in our model:
- If the reservation was successful the rcvbox is checked to determine if the scheduling agent has received an answer from all the participants their agendas. Thanks to the reïfication of the communication traces by the mailboxes there is no need to manually maintain the progress of the meeting scheduler. If all agendas are successfully reserved, then the ScheduleAgent actor sends confirm messages to all agendas.
- If an individual reservation request fails then the scheduler agent has to free up the slots of the reservations that were successful. The sentbox can be used to track to which agenda actors the scheduler agent has already sent reservation request. These actors are sent a free message so that they can undo their reservation. Furthermore, the scheduler agent deletes the reservation messages from the outbox and thereby undoes the communication before it occurred. Next, the scheduler agent also notifies the customer actor that sent the schedule message that the meeting could not be scheduled by sending it a failed message.
if(and(disjoin?(m),
eq?( map(sender, filter(confirm?, messages('sentbox)))),
participants))
seq(send(customer, mkSucceeded()),
become(
seq(handleJoin(m),
become(b(id, participants, customer)))))
Each time the ScheduleAgent actor disjoins from an agenda actor it checks to see if all confirm messages were sent out, again using the sentbox. If all confirm messages were sent, then the customer actor that sent the schedule is notified with a succeeded message.
The second example has shown that the mailboxes, which reïfied the communication traces, introduced in the ambient actor model contain primitives that allow the scheduler agent to deal with the autonomous and concurrent nature of the devices. Indeed, the scheduler agent consults and manipulates its outbox and sentbox to keep pace with the communication status of the different messages. Note that the implementation above relies on the eventual delivery of messages. More advanced delivery policies can be devised for this application based on the manipulation of mailboxes. For example, a broken connection between applications could be intercepted with a disjoin message and unsent reservation requests could be reversed by removing them from the outbox.
5. Model Evaluation
We discussed the actor model in the light of requirements introduced through mobile ad-hoc networking and, although the model provides non-blocking communication primitives and an isolated data-model, we concluded that the model lacks reïfied communication traces and reïfied environmental context. The lack of support for these two criteria made standard actors unsuitable for mobile ad-hoc networking. The ambient actor model resolves these restrictions with the introduction of explicit mailboxes. The use of such mailboxes is twofold: making the communication state of an actor explicit and allowing for acquaintance management. Both uses are detailed below.5.1. Communication State
When scrutinising the communication structure of the actor model, we can distinguish between four types of messages. The first type of messages are those an actor received but still needs to process, called cool messages. A second type of messages are those the actor has sent but that have not yet been transmitted. Those are called square messages. Third, there are messages that an actor has received and processed, termed groovy messages. Finally, there are the messages that an actor has sent and transmitted. Those messages are termed hip messages. Together, these four types of messages describe the complete communication trace of an actor over time. Likewise, we can classify actors based on the kind of messages they have queued. Ambient actors that have mainly incoming messages to be handled are termed cool. Ambient actors that have mainly processed messages are termed groovy. Actors that mainly transmit messages are termed hip and those that want to transmit but seem to get nowhere are termed square. Such classification is useful to study the operational properties of interconnected systems. The overall process scheduling should limit the number of square and cool actors, and focus on a stable balance between hip and groovy ones.In contrast to the standard actor model, where every actor merely has an implicit message set for accumulating incoming and outgoing messages, the ambient actor model allows clear distinction of these four types of messages by introducing four explicit mailboxes. The messages of the first type are put in the mailbox inbox, the second type of messages are put in the mailbox outbox. If an actor receives a message, then that message will be put in the mailbox inbox, waiting to be processed by that actor. When a message is sent by an actor it is put in its mailbox outbox, waiting to be transmitted to the recipient of that message.
Both mailboxes inbox and outbox are implicitly present in the actor model and enable non-blocking communication as argued in section 3.1.
In addition to the mailboxes inbox and outbox there are two more mailboxes, rcvbox and sentbox, for the third and fourth type of messages respectively. In the ambient actor model, when a message is processed it is moved from the mailbox inbox to the mailbox rcvbox and when a message is actually transmitted to another actor, then the message is moved from the mailbox outbox to the mailbox sentbox.
Conceptually, the mailboxes rcvbox and sentbox allow one to have a peek in the past of the communication history of an actor. Note that the mailboxes inbox and outbox of the actor represent its continuation, because these two mailboxes contain the messages it will process and transmit in the future. Hence, through the introduction of these four explicit mailboxes we have a gate to the past and the future of the actor's state of communication, which enables the reïfied communication traces that were argued in section 3.1.
The ambient actor model provides explicit control over the communication state of an actor through mailbox manipulations. Apart from the four mailboxes that control the communication state, every actor can create custom mailboxes. Messages can reside in multiple mailboxes at the same time. The status of the delivery of a message can be monitored and altered by accessing the appropriate mailbox. For example, by removing a message from the mailbox out we can stop the message from being delivered. Hence, by giving access to the mailboxes, first-class continuations are attained. The mailboxes in and out not only allow one to have a peek in the future computation and communication of the actor, but even to manipulate it. For example, we could remove a message from the mailbox in and thereby prevent it from being processed by the actor.
5.2. Acquaintance Management
In section 3.1 we argued that a form of acquaintance management should be possible in languages targeting mobile ad-hoc networks. In the ambient actor model, distributed naming is available via a pattern-based lookup mechanism. A pattern is an abstract description of a set of actors and is specified by a communicable value. An actor that wants to search for certain other actors in its environment places a corresponding pattern in its mailbox required. Conversely, when an actor wants to make itself available for other actors it places a pattern with a description of itself in its mailbox provided. In the former case the actor is said to require a pattern, while in the latter case the actor is said to provide a pattern. Multiple patterns can be added to a mailbox such that an actor can require or provide multiple patterns simultaneously. A pattern can also be removed from either mailboxes at any time when the actor no longer requires or provides a certain pattern.When two or more actors enter one another each communication range and have a corresponding pattern in their provided and required mailboxes, the mailbox joined of the actor that required the pattern is updated with a resolution. Such a resolution is a pair consisting of the pattern and a reference to the actor who provided the pattern. Conversely, when two actors with a corresponding pattern in their mailboxes are pulled out of communication range, the resolution is moved from the mailbox joined to the mailbox disjoined. This mechanism allows actors not only to detect new resources in its environment, but also to detect when actors disappeared from the environment. Through this mechanism an actor can manage its acquaintances.
5.3. Intra-actor concurrency
By adopting actors as a foundation for ubiquitous actors, we inherited the asynchronity found in the original actor model. However, because we prohibit the further use of an actor after become we removed intra-object concurrency and thus reduce the massive parallelism that was found in the actor model. We do not believe that the change influences the workability of the actor model for mobile ad-hoc networks.In fact, many contemporary implementations of programming languages based on the actor model have made a similar trade-off. In languages such as Salsa [44] and E [26] the become operation has been replaced by assignments that are used throughout a method body. In these languages the intra-object concurrency has also been removed to ensure that no race conditions occur on the internal state of the actor.
5.4 Usability of the model as a direct programming language
Up to now we have shown that the ambient actor model provides the necessary abstraction for programming in mobile ad-hoc networks. This was illustrated in the meeting scheduler case 4.2. However, some of the implementation details indicate that the object model lacks expressiveness (in the sense that most operations provide only the necessary functionality). Unfortunately, this lack of expressiveness is inherited from the ``object model'' of the standard actor model. For example, an actor that uses of the psend abstraction must also manually incorporate the handleJoin in its behavior such that it understands the join messages and can handle them accordingly. In the code, the reserveScheduleAgent and the ConfirmScheduleAgent behaviors both had to embed this handler. In [45] we explored this path further.5.5. Continuations vs Computational Traces
In many respects first-class mailboxes can be regarded as a representation of first-class continuations for the actor model. In sequential languages first-class continuations can be used to implement many high-level abstractions, such as exception handling systems and co-routines. However, unlike most of these high-level abstractions, first-class continuations themselves are cumbersome to use and sometimes difficult to understand. The mailboxes as presented here make this concept much more accessible.6. Future Work
Given our experience with this model in various contexts [33, 34], we found that most actors behave as state machines. Based on this knowledge, we currently work on a merge of colored Petri-nets [46, 47, 48] into the ambient actor formalism as a means to formally describe and analyze the properties of the system or parts of the system. This includes at different levels of detail: the allowed/expected/provided/required (abbreviated AEPR) state transitions within actors running on an actor system; the AEPR state transitions of the actor system running on a device; and at runtime the AEPR state transitions of joined actor configurations. The adoption of such formalism will make automatic interface validation possible, and might lead to automated conflict resolution [49, 50].7. Conclusion
Putting the ambient actor model in perspective, it forms a formalism that integrates the restrictions imposed by mobile ad-hoc networks and the wish to freely communicate between actors in the vicinity. We extended the operational semantics of the standard actor model in order to deal with three problems associated with mobile (ad-hoc) networks:
- How to deal with local resources?
To handle this problem we introduced reduction rules join and disjoin that specify what happens when devices come in communication range of one another. - How to deal with volatile connections?
This problem is handled with the introduction of the inbox, rcvbox, outbox and sentbox mailboxes that allow one to track and intervene in the communication between different devices. - How to deal with the autonomous nature of interactions?
This is handled through the manipulation of mailboxes that reïfy the communication traces and through the manipulation of custom mailboxes.
The novelty of our approach lies in the combination of a) mailboxes, b) pattern matching on actor descriptors and c) the automatic joining and disjoining of configurations.
Bibliography
| 1. | {T}he {C}omputer for the 21st {C}entury M. Weiser Scientific {A}merican; {S}cientific {A}merican; volume: 265; number: 3; pages: 66-75; 1991 |
| 2. | Specification of the Bluetooth System; Wireless Connection Made Easy. N.A. Bluetooth Special Interest Group (SIG), November 2003. |
| 3. | 802.11 Wireless Networks: The Definitive Guide {M}atthew {S}. {G}ast O'Reilly; 1 edition; isbn: 0596001835; April; 2002 |
| 4. | {S}ensor {N}etwork {T}echnologies and {A}pplications {Intel Cooperation} howpublished: Internet; url: http://www.intel.com/research/exploratory/motes.htm; 2006 |
| 5. | {S}martMesh {S}ystem {C}omponents Dust Networks Inc howpublished: Internet; url: http://www.dustnetworks.com/products/main.shtml; 2006 |
| 6. | Time, clocks, and the ordering of events in a distributed system. Leslie Lamport Communications of the ACM; volume: 21; number: 7; pages: 558-656; 1977 |
| 7. | {S}mart {B}uildings {A}dmit their {F}aults David Pescovitz Public Affairs Office of the UC Berkeley College of Engineering; institution: UC Berkeley College of Engineering; url: http://www.coe.berkeley.edu/labnotes/1101smartbuildings.html; 2001 |
| 8. | Amorphous {C}omputing Harold Abelson, Don Allen, Daniel Coore, Chris Hanson, George Homsy, Thomas F. Knight, Redhika Nagpal, Erik Rauch, Gerald J. Sussman, Ron Weiss Communications of the {A}CM; volume: 43; number: 5; pages: 74-82; 2000 |
| 9. | RFC 2608: Service Location Protocol, Version 2 E. Guttman, C. Perkins, J. Veizades, M.Day number: 2608; institution: The Internet Society; June; 1999 |
| 10. | Scenarios for {A}mbient {I}ntelligence in 2010 K. Ducatel, M. Bogdanowicz, F. Scapolo, J. Leijten, J.C. Burgelman IPTS-Sevile, see http://www.cordis.lu/ist/istag.htm; February; 2001 |
| 11. | Generative Communication in {Linda} David Gelernter ACM Transactions on Programming Languages and Systems; volume: 7; number: 1; pages: 80-112; coden: ATPSDT; issn: 0164-0925; keywords: design; languages; theory; subject: {\bf D.3.2}: Software, PROGRAMMING LANGUAGES, Language Classifications, Linda. {\bf C.2.1}: Computer Systems Organization, COMPUTER-COMMUNICATION NETWORKS, Network Architecture and Design, Network communications. {\bf D.3.4}: Software, PROGRAMMING LANGUAGES, Processors, Compilers. {\bf D.3.3}: Software, PROGRAMMING LANGUAGES, Language Constructs and Features, Concurrent programming structures. {\bf D.4.4}: Software, OPERATING SYSTEMS, Communications Management, Message sending. {\bf D.1.3}: Software, PROGRAMMING TECHNIQUES, Concurrent Programming. {\bf C.2.4}: Computer Systems Organization, COMPUTER-COMMUNICATION NETWORKS, Distributed Systems, Distributed applications. {\bf D.4.2}: Software, OPERATING SYSTEMS, Storage Management, Distributed memories.; jan; 1985 |
| 12. | Linda in context Nicholas Carriero, David Gelernter {Communications of the ACM}; ACM Press; volume: 32; number: 4; issn: 0001-0782; pages: 444-458; 1989 |
| 13. | Locality Based {Linda}: Programming with Explicit Localities R. De Nicola, G. Ferrari, R. Pugliese Lecture Notes in Computer Science; volume: 1214; pages: 712-??; coden: LNCSD9; issn: 0302-9743; bibdate: Fri Aug 22 11:59:49 MDT 1997; acknowledgement: ack-nhfb; 1997 |
| 14. | Mobile Ambients Luca Cardelli, Andrew D. Gordon Electronic Notes in Theoretical Computer Science; Elsevier; volume: 10; editor: Andrew Gordon and Andrew Pitts and Carolyn Talcott; 2000 |
| 15. | A Calculus of Mobile Agents C. Fournet, G. Gonthier, J. J. Levy, L. Maranget, D. Remy Proceedings of 7th International Conference on Concurrency Theory (CONCUR'96); Springer-Verlag; pages: 406-421; series: LNCS; editor: U. Montanari and V. Sassone; volume: 1119; address: Berlin, Germany; aug; 1996 |
| 16. | A Calculus of Mobile Processes, Part I + II R. Milner, J. Parrow, D. Walker Information and Computation; volume: 100; number: 1; pages: 1-77; 1992 |
| 17. | Communicating and Mobile Systems: the Pi-calculus Robin Milner Cambridge University Press; May; 1999 |
| 18. | Viewing Control Structures as Patterns of Passing Messages Carl Hewitt Artificial Intelligence; volume: 8; number: 3; pages: 323-364; keywords: concurrency messages actors binder; jun; 1977 |
| 19. | Actors - A Model of Concurrent Computation for Distributed Systems G. Agha MIT Press; 1986 |
| 20. | Concurrent Programming using Actors Gul Agha, Carl Hewitt Object-Oriented Concurrent Programming; The MIT Press: Cambridge, MA, USA; editor: A. Yonezawa and M. Tokoro; series: Computer Systems Series; pages: 37-53; 1988 |
| 21. | A Foundation for Actor Computation Gul Agha, Ian A. Mason, Scott F. Smith, Carolyn L. Talcott Journal of Functional Programming; Cambridge University Press; volume: 7; number: 1; pages: 1-72; 1997 |
| 22. | Concurrent object-oriented programming Gul Agha Communications of the ACM; ACM Press; volume: 33; number: 9; issn: 0001-0782; pages: 125-141; 1990 |
| 23. | Computational lambda-calculus and monads E. Moggi Proceedings of the Fourth Annual Symposium on Logic in computer science; IEEE Press; isbn: 0-8186-1954-6; pages: 14-23; location: Pacific Grove, California, United States; address: Piscataway, NJ, USA; 1989 |
| 24. | Scheme: an Interpreter for Extended Lambda Calculus Gerald Jay Sussman, Guy L. Steele Jr. Mass. Institute of Technology, Artificial Intelligence Laboratory, Cambridge; December; 1975 |
| 25. | Equivalence in Functional Languages with Effects Ian Mason, Carolyn Talcott Journal of Functional Programming; key: Mason \& Talcott; volume: 1; number: 3; pages: 287-328; annote: Adds objects with memory to a call-by-value lambda calculus. 43 references.; jul; 1991 |
| 26. | The {E} Programming Language, the secure distributed pure-object platform and p2p scripting language for writing Capability-based Smart Contracts. Mark Miller note: http://www.erights.org; 2004 |
| 27. | Object Serialisation for Marshalling Data in a Java Interface to MPI Bryan Carpenter, Geoffrey Fox, Sung Hoon Ko, Sang Lim Java Grande; pages: 66-71; 1991 |
| 28. | Flick: A Flexible, Optimising IDL Compiler Eric Eide, Kevin Frei, Bryan Ford, Jay Lepreau, Gary Lindstrom {SIGPLAN} Conference on Programming Language Design and Implementation; pages: 44-56; 1997 |
| 29. | {CORBA} {F}undamentals and {P}rogramming Jon Siegel, {A}lan Klein, {A}lex Thomas, Dan Frantz, Hal Mirsky John Wiley and Sons (Inc), New York; isbn: 0471121487; pages: 693; {A}pril; 1996 |
| 30. | ActorSpace: an open distributed programming paradigm Gul Agha, Christian J. Callsen PPOPP '93: Proceedings of the fourth ACM SIGPLAN symposium on Principles and practice of parallel programming; ACM Press; isbn: 0-89791-589-5; pages: 23-32; location: San Diego, California, United States; 1993 |
| 31. | Capability-Based Computer Systems Henry M. Levy Butterworth-Heinemann; isbn: 0932376223; address: Newton, MA, USA; 1984 |
| 32. | Actors for Mobile Ad-Hoc Networks Jessie Dedecker, Werner Van Belle Embedded and Ubiquitous Computing; Springer; editor: Yang, L.T. and Guo, M. and Gao, G.R. and Jha, N.K.; note: Embedded and Ubiquitous Computing, International Conference EUC 2004, Aizu-Wakamatsu City, Japan, August 25-27, 2004; series: Lecture Notes in Computer Science; volume: 3207; isbn: 3-540-22906-X; pages: 482-494; 2004 |
| 33. | Experiences in Mobile Computing: The CBorg Mobile Multi-Agent System Werner Van Belle, Johan Fabry, Theo D'Hondt, Karsten Verelst Proceedings TOOLSEE 2001, Zurich; IEEE Computer Society Press; pages: 1-9; volume: 38; address: http://borg.rave.org/; editor: Wolfgang Pree; March; 2001 http://werner.yellowcouch.org/Papers/expmobcom/index.html |
| 34. | The Component System Werner Van Belle, David Urting institution: Technical Report 3.4 for the {SEESCOA} project, Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussel, Belgium; October 2000, http://www.cs.kuleuven.ac.be/cwis/research/distrinet/projects/SEESCOA |
| 35. | Going Beyond the Sandbox: An Overview of the New Security Architecture in the Java Development Kit 1.2 L. Gong, M. Mueller, H. Prafullchandra, R. Schemers {USENIX} Symposium on Internet Technologies and Systems; address: Monterey, C{A}; pages: 103-112; 1997 |
| 36. | {Ontologies as Conceptual Models for XML Documents} Michael Erdmann, Rudi Studer institution: Institut fur {A}ngewandte Informatik und Formale Beschreibungsverfahren ({AIFB}) University of Karlsruhe (TH) D-76128 Karlsruhe (Germany) \{erdmann, studer\}@aifb.uni-karlsruhe.de |
| 37. | Is XML really enough ? R. Behrens, G. Buntrock, C.Lecon, V.Linnemann number: {A}-99-11; institution: Institut {f\"ur} Informationssysteme, Osterweide 8, 23562 {L\"ubeck} Medizinische {Universit\"at}, Germany; 1999 |
| 38. | {KQML} as an Agent Communication Language T. Finin, R. Fritzson, D. McKay, R. McEntire Proceedings of the 3rd International Conference on Information and Knowledge Management ({CIKM}'94); ACM Press; address: Gaithersburg, MD, USA; editor: N. Adam and B. Bhargava and Y. Yesha; pages: 456-463; 1994 |
| 39. | Implementing Remote Procedure Calls A. D. Birrell, B. J. Nelson Proceedings of the {ACM} Symposium on Operating System Principles; Association for Computing Machinery; address: Bretton Woods, NH; pages: 3; 1983 |
| 40. | A distributed object model for the { Java }System A. Wollrath, R. Riggs, J. Waldo 2nd Conference on Object-Oriented Technologies \& Systems ({COOTS}); {USENIX} Association; pages: 219-232; 1996 |
| 41. | Many-to-Many Invocation: A new object oriented paradigm for ad hoc collaborative systems. Alan Kaminsky, Hans-Peter Bischof 17th Annual ACM Conference on Object Oriented Programming Systems, Languages, and Applications (OOPSLA 2002); ACM Press; 2002 |
| 42. | Scheme: An Interpreter for Extended Lambda Calculus Gerald Jay Sussman, Guy L. Steele Jr. Higher-Order and Symbolic Computation; volume: 11; number: 4; pages: 405-439; coden: LSCOEX; issn: 1388-3690; bibdate: Sat Jul 17 17:47:05 MDT 1999; url: http://www.wkap.nl/oasis.htm/193825; acknowledgement: ack-nhfb; dec; 1998 |
| 43. | Structure and Interpretation of Computer Programs Harold Abelson, Gerald J. Sussman MIT Press; isbn: 0262011530; address: Cambridge, MA, USA; 1996 |
| 44. | Programming dynamically reconfigurable open systems with SALSA Carlos Varela, Gul Agha ACM SIGPLAN Notices; ACM Press; volume: 36; number: 12; issn: 0362-1340; pages: 20-34; 2001 |
| 45. | Ambient-{O}riented {P}rogramming in {A}mbient{T}alk Jessie Dedecker, Tom Van Cutsem, Stijn Mostinckx, Theo D'Hondt, Wolfgang De Meuter ECOOP 2006: European Conference on Object-Oriented Programming; address: Nantes, France; July; 2006 |
| 46. | Comunication by Means of Automata (Kommunikation mit Automaten) Petri, C.A. Schriften des IIM, vol 2; 1962 |
| 47. | {{A}n Introduction to the Theoretical {A}spects of Coloured Petri Nets} K. Jensen {A} Decade of Concurrency; Springer Verlag; editor: J.W. de Bakker and W.P. de Roever and G. Rozenberg; series: Lecture Notes In Computer Science; volume: 803; pages: 230-272; 1994 |
| 48. | {The Practitioner's Guide to Coloured Petri-nets} Lars M. Kristensen, S{\/o}ren Christensen, Kurt Jensen International Journal on Software Tools for Technology Transfer; Springer-Verlag; pages: 98-132; 1998 |
| 49. | Formal Specification and Prototyping of CORBA Systems R. Bastide, O.Sy., P. Palanque Proceedings of ECOOP'99; Spring Verlag LNCS 1628; pages: 474-494; 1999 |
| 50. | Creation of an Intelligent Concurrency Adaptor in order to mediate the Differences between Conflicting Concurrency Interfaces Werner Van Belle school: Vrije Universiteit Brussel; September; 2003 |
| http://werner.yellowcouch.org/ werner@yellowcouch.org |  |