Two Solutions to Harmonics due to short Envelope Fades.

Werner Van Belle¹ - werner@yellowcouch.org, werner.van.belle@gmail.com

1- Yellowcouch;

Abstract : When dealing with audiosignals, often a tone of known frequency must be faded in or out (for e:g suppression of ringing, or attack times of compressors). When the period used to fade in the tone is sufficiently short, overtones are created. We prove that only two fade in times canbe used to only have harmonics that are octaves apart. The first solution (a fade time of half the primary frequency) produces an harmonic 1 octave higher. The second (a fade time of a sixth period), produces harmonics at 1 octave and 2 octaves higher. No other solutions exist.

Keywords: transients, attack, envelope, gain modification, harmonics
Reference: Werner Van Belle; Two Solutions to Harmonics due to short Envelope Fades.; Audio Processing; YellowCouch; January 2014

Table Of Contents

Introduction
Only two solutions exist
    m<0
    m=0
    m>0 & m<1
    m>=1

Graphics
Conclusion

Introduction

When dealing with audiosignals, often a tone of known frequency must be faded in or out (for e:g suppression of ringing, or attack times of compressors). When the period used to fade in the tone is sufficiently short, overtones are created. Below we analytically investigate which overtones and how we can choose a fade time that procuded only harmonics at distances of octaves.

First we need some definitions of the waves we are talking about. The signal that we want to fade in is called x and has a radian frequency of omega.

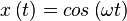
The edge (e) we will use to fade has the shape of half a sinus (the strictly increasing part) and has a frequency that is related to omega by a factor m. The signal is offset with a DC as to have a gain from 0 to 1

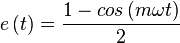
at 0 e(0) is 0 at 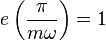, which means that the transition spans 1/2m of the period of x(t).

The edge is applied to the signal through multiplication, which gives

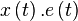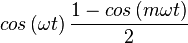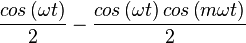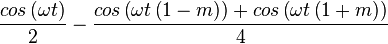Which shows us that during the transition, the main signal will be played at -6dB (0.5cos(omega.t)), and have two harmonics at -12dB. The first harmonic will be at 1-m times the frequency of x(t), the second harmonic will be at 1+m times the frequency of x(t).

Now we would like to know how we can choose m such that the harmonics are octaves apart. That means that |1+m| and and |1-m| are integer powers of two. E.g, with m=1, we have 0 and 2, both. With m=3, we have 4 and |-2|.

Only two solutions exist

Oddly, these two examples also finish the range of possibilities. There are only 2 solutions to fade in a note without introducing non-octave harmonics. The first thing to note is that it is not because 1-m and 1+m must be integer powers of two that m must be an integer. So let's investigate the range of possible values for m.

m<0

Suppose n=-m, then n will be strictly positive, and the two harmonics will be |1-n| and |1+n|, or |1+m| and |1-m|. Which shows that the two harmonics simply swapped place. So all cases of m<0 can be found back in the negated versions.

m=0

makes no sense because the transition period \frac{1}{2m} would be \infty. Not realizable.

m>0 & m<1

In this case, the |1+m| harmonic is always positive. To realize an octave change of B, m must be

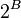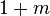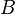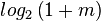Given that 1+m a strictly increasing function is and that the logarithm also a strictly increating function is, we can set the bounds for B as

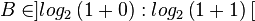
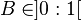
Within this range, no integer value for B exists.

m>=1

When m is >= 1, we can drop the two absolute values. And work with the harmonics m-1 (=|1-m| ) and m+1=|1+m|. The octave increase is given as

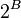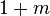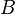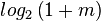Again m+1 is strictly increasing, so is log_2, which thus defines the bounds on B to be

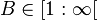
Within that range an infinite amount of integers can be found. Whether they are all useful is a bit in question (shifting thing 50 octaves up ?), but that shouldn't stop us from figuring out for which values of m>=1, B and its accompanying harmonic A, will be an integer.

The secondary harmonic is defined as

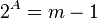
Combining the definitions of A and B, we get

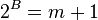
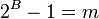
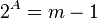
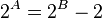
From this equation, it is clear that A < B. We now set out to prove that B<=2. To prove this, we look at the difference between 2^{B} and 2^{A}

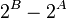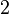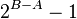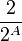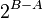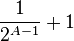Given that B and A are distinct integers and that 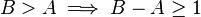and thus that 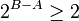. continuing from the above equation

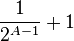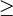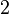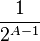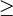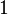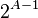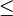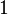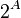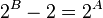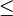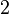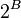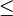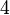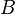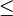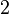The two and only integers that satisify B>=1 and B<=2 are 1 and 2.

In case B=1, m=1, and A equals -\infty. The first harmonic is thus 1 octave higher, while the second results in a DC offset added to the signal (which we actually did by adding 0.5). This does however not add any visible nor audible effects.

In case B=2, m=3 and A=1. We will thus have harmonics 1 octave and 2 octaves higher.

Graphics

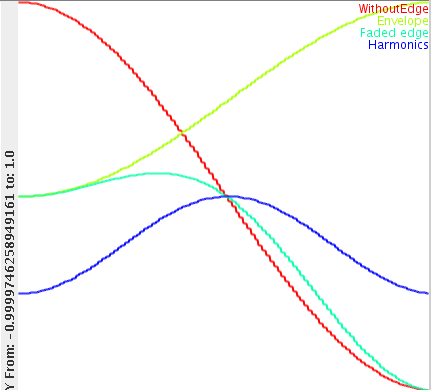Demonstration og the effect of a period/2 gain envelope.

In the above image, the red line is part of the tone that has to be faded in. The envelope we will apply is drawn in yellow (lime ?). The multiplication of the envelope with the tone is plotted in turquoise. After subtracting the turquoise from the original (red) signal, we see the harmonics produced by this fade in. As can be seen, the red part of the wave is half a period long. The blue wave (the harmnic) on the other hand is exactly one period.

Practically, if you have a bass at 50Hz (equals a period of 20 milliseconds) and you would like a short punchy attack, you either use a 10msecs attack (which is not uncommonly heard), or a 3.333msecs attack. The latter will introduce two octaves at the point of fade in. Of course, since it is only 3.3 milliseconds it might not matter very much. Pragmatically, it seems that the 1/6 solution is not really valuable.

Conclusion

We showed that in order to fade in or fade out a tone of specific frequency f, without introducing unwatned harmonics during the transition time, one must choose either a) transition times of multiple seconds, or b) transition times that are half a frequency f, in which case a harmonic that is 1 octave higher will be added, or c) transition times that are a sixth period of frequency f, in which case the harmonics will be 1 and 2 octaves higher.

http://werner.yellowcouch.org/
werner@yellowcouch.org