An Auditory Overview of some Infinite Impulse Response (IIR) Filters.

Werner Van Belle¹ - werner@yellowcouch.org, werner.van.belle@gmail.com

1- Yellowcouch;

Abstract : For a number of IIR filters we show their frequency responses and demonstrate their effect on audio.

Keywords: iir, butterworth, butterworth bandpass, chebyshev 1, chebyshev 2, biquad
Reference: Werner Van Belle; An Auditory Overview of some Infinite Impulse Response (IIR) Filters.; Audio Processing; YellowCouch; September 2012

Table Of Contents

Introduction
Biquads
    Peak
    Low shelve
    High shelve, smaller Q
Butterworths
    Standard 10th order lowpass
    Standard 10th order highpass
    Not so standard band modification filters

Chebyshev Type 1
    8th order lowpass
    8th order highpass
Chebyshev Type 2
    8th order lowpass
    8th order highpass
References

Introduction

While working at Audiotool, I created a number IIR filters. IIR stands for infinite impulse response. They are created by feeding the output of the filter back into its input. The result is that each filter coefficient acts on the signal for a long time, which thus means that a long impulse response can be generated using a small number of coefficients. In other words, few calculations, great result.

Below, I demonstrate some of the filters I encountered. Each filter its frequency response is visualized as a red line. The blue line is the measured frequency response of the audio-output (that is the Fourier transform of the filtered signal). Each frequency response is shown on a logarithmic scale (from left to right we have thus octaves, each vertical line is the next octave, with 440 Hz being the middle of the 4th octave (A4)). Vertically, the gain (in dB) is set out. Under each image the filtered audio can be heard.

The audio samples are from the song 'Chamber' by André Michelle (see http://www.audiotool.com/track/chamber/ for the original). All filters are bilinear transforms of their analog counterparts.

Biquads

Biquads can be readily implemented using Bristow-Johnsons Audio EQ cookbook. A must read for anyone starting out in the digital filter domain

Biquads are good for resonating and sweeping filters, they are not particularly well suited to create high quality lowpass or highpass filters, although a soft shelving of the higher frequencies might sometimes be useful in a mastering setting

Peak

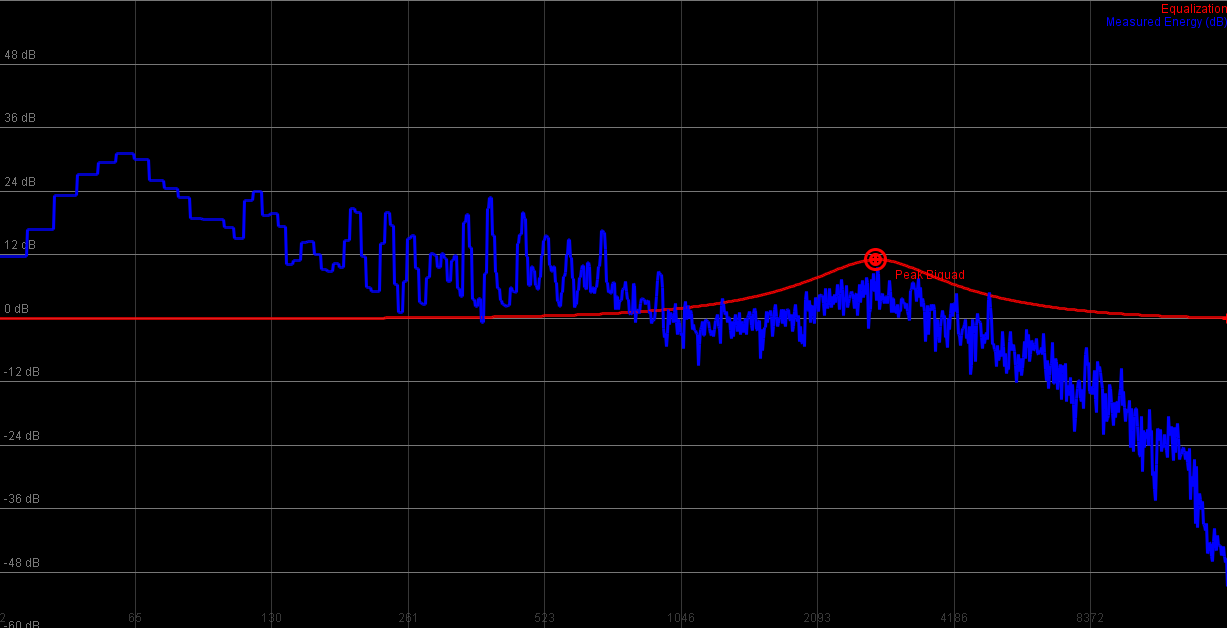
Low shelve

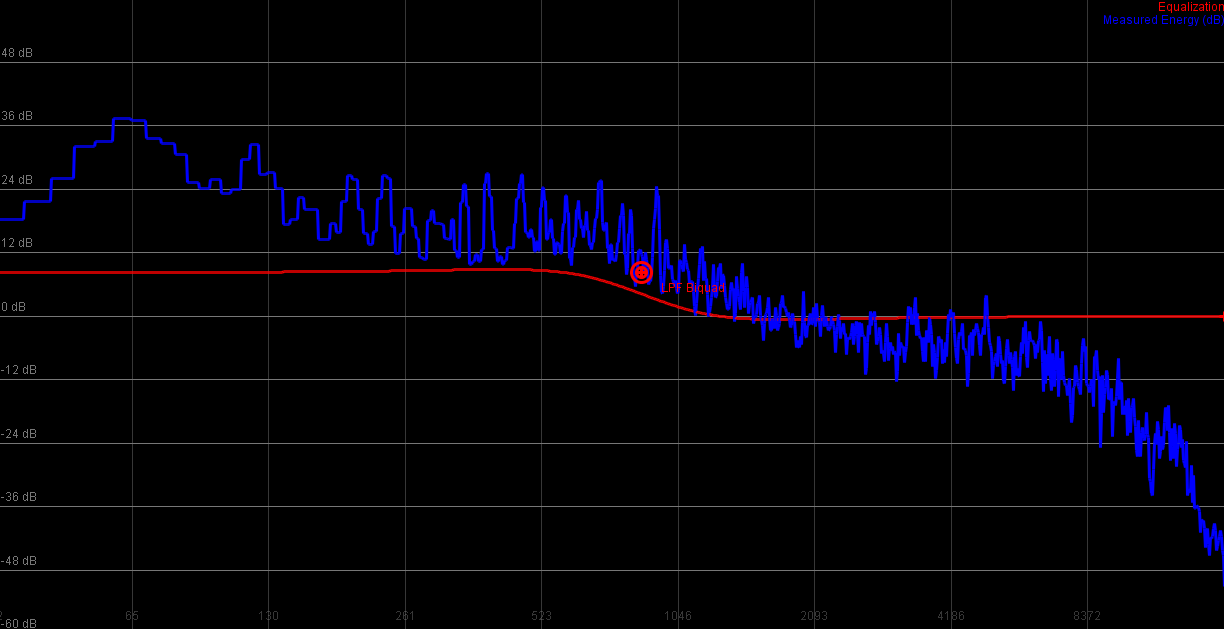
High shelve, smaller Q

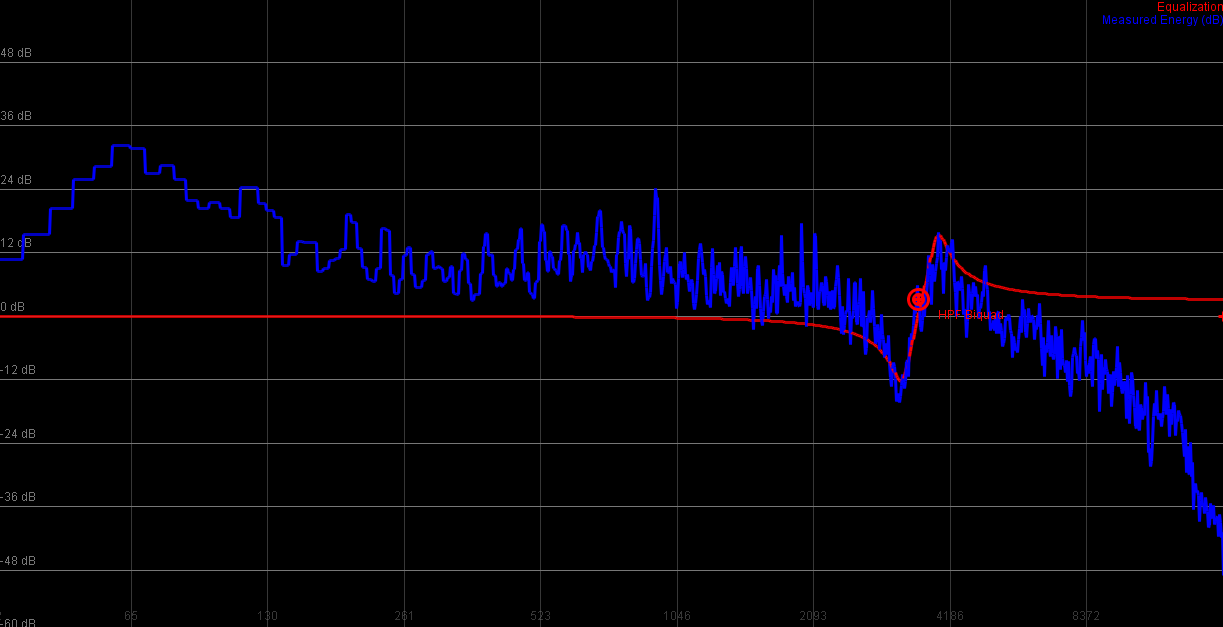
Butterworths

Butterworth filters form maximal flat passbands, a very nice feature and form the perfect tool to create good general purpose sweeping lowpass/highpass filters. E.g: a sweep from low to high has a rather Daft Punk feeling.

The scientific curious will find Butterworths' original paper [1] an interesting read.

An interesting side usage of butterworth filters is the creation of a crossover for speakers. In that case the high frequencies are the result of an even number of butterworth highpass filters, while the lower frequencies are the result of the same number of lowpass filters. This type of crossover is called a Linkwitz-Rilley [2]

Standard 10th order lowpass

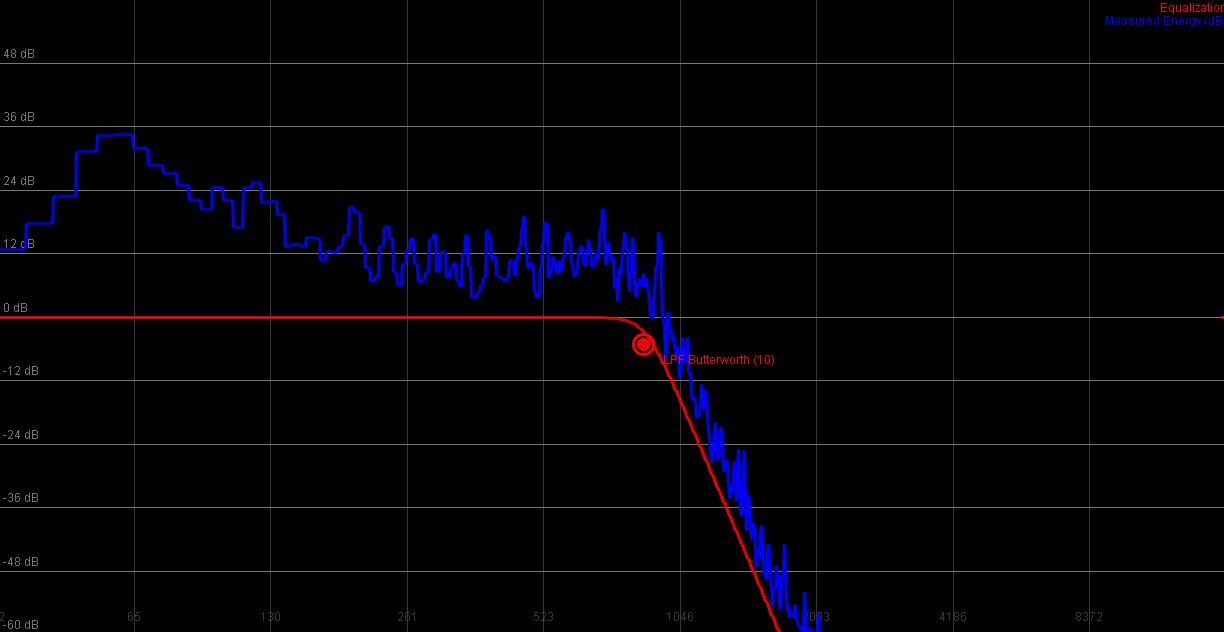
Standard 10th order highpass

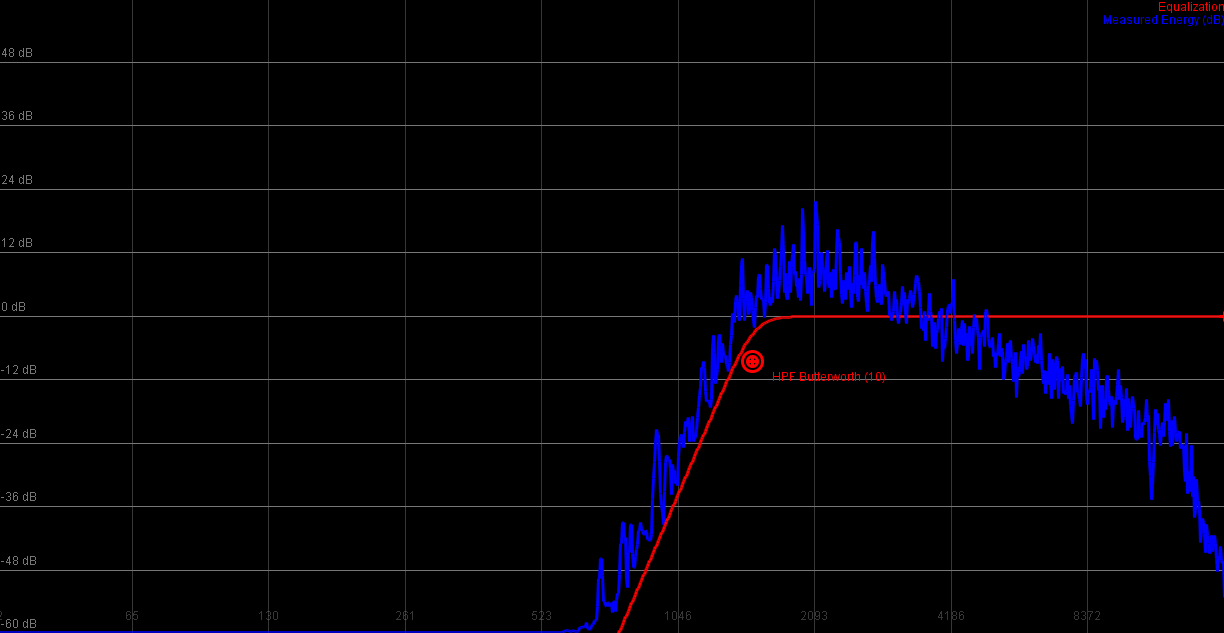
Not so standard band modification filters

Although it is fairly common to find lowpass, or highpass, or even bandpass implementations of butterworth filters; it was not as easy to create one that would allow us to specify the passband gain and the stopband gain separately. Based on work by Miller Puckette [3], I was able to make this work and am quite happy with the sonic result.

For higher frequencies it adds a fair amount of resonance to the result, which is very nice when working with noise sounds & guitars.

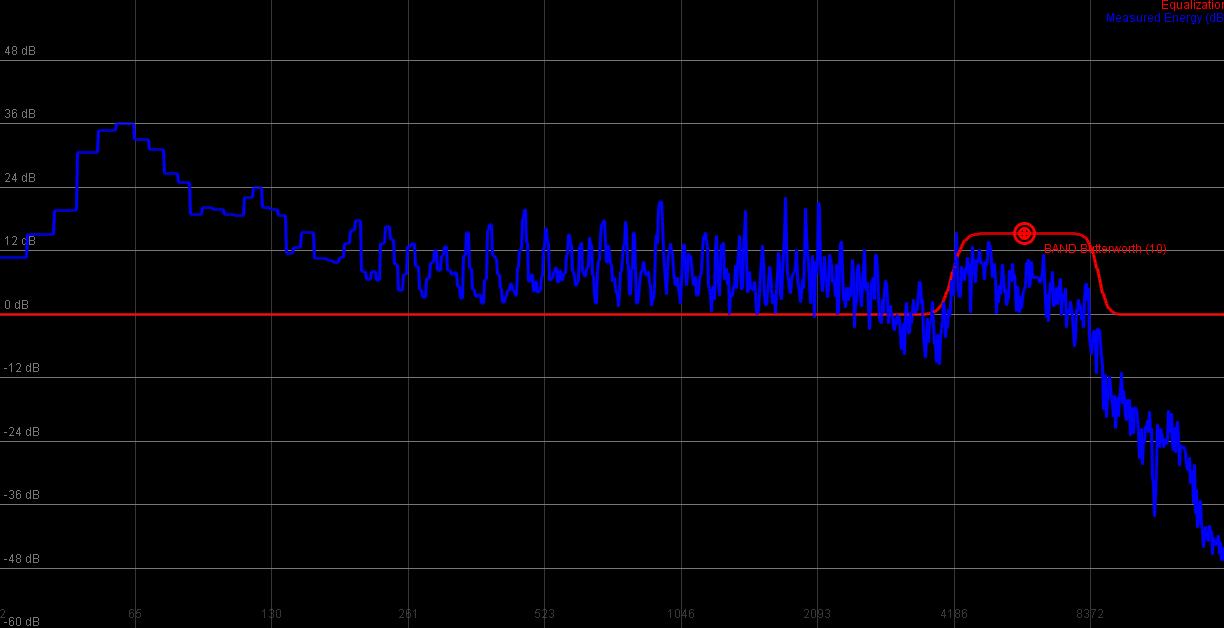
For lower frequencies it is certainly 'interesting'. The group delay of the different frequencies is so out of whack that the bassdrum suddenly sounds as if it were created by a dancing deep-sea turtle.

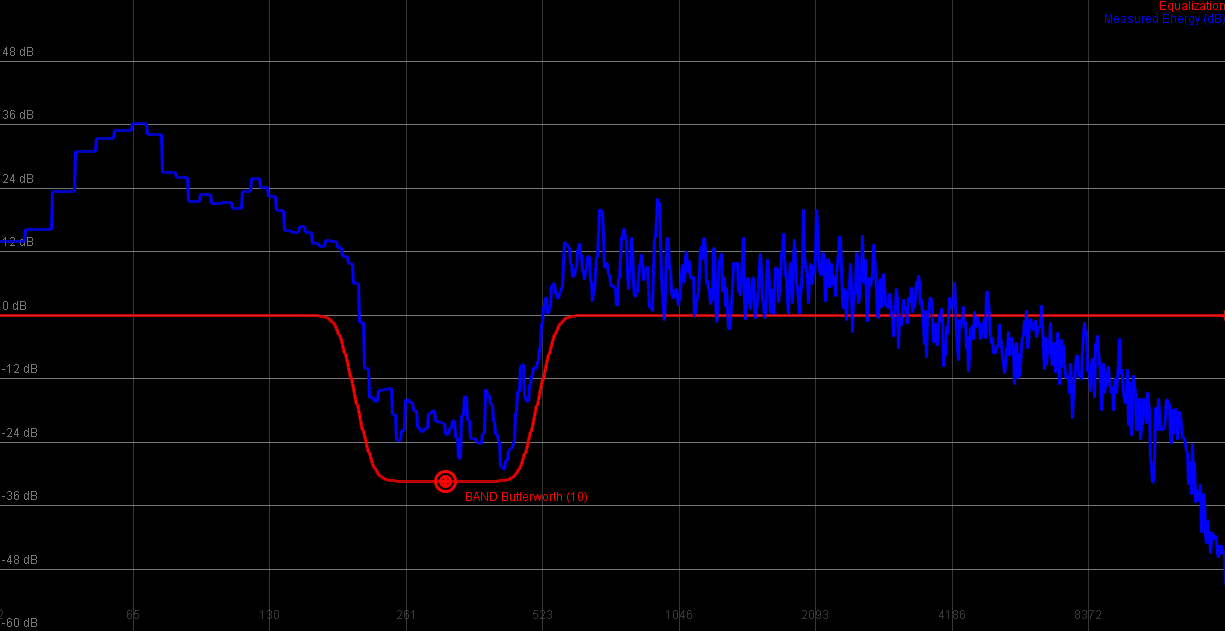
Chebyshev Type 1

Although Chebyshev filters can be used to create lowpass and highpass filters, their transition is fairly abrupt, which results in audible distortion. A Chebyshev type 1 filter is defined with a passband ripple, which provides for a good effect filter.

8th order lowpass

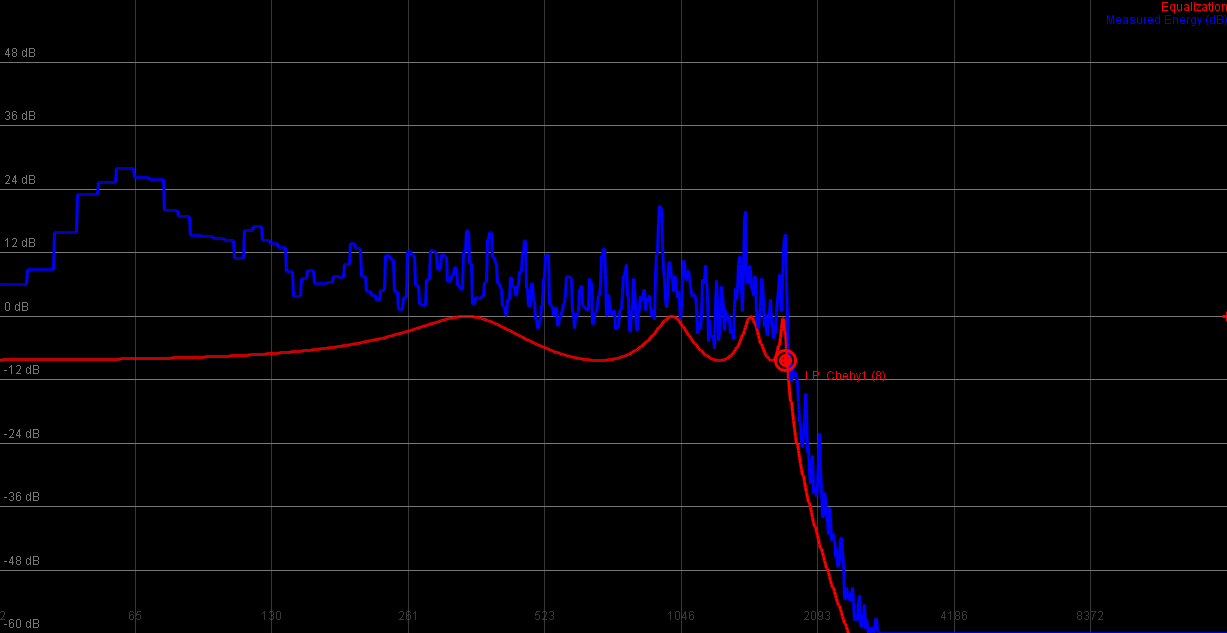
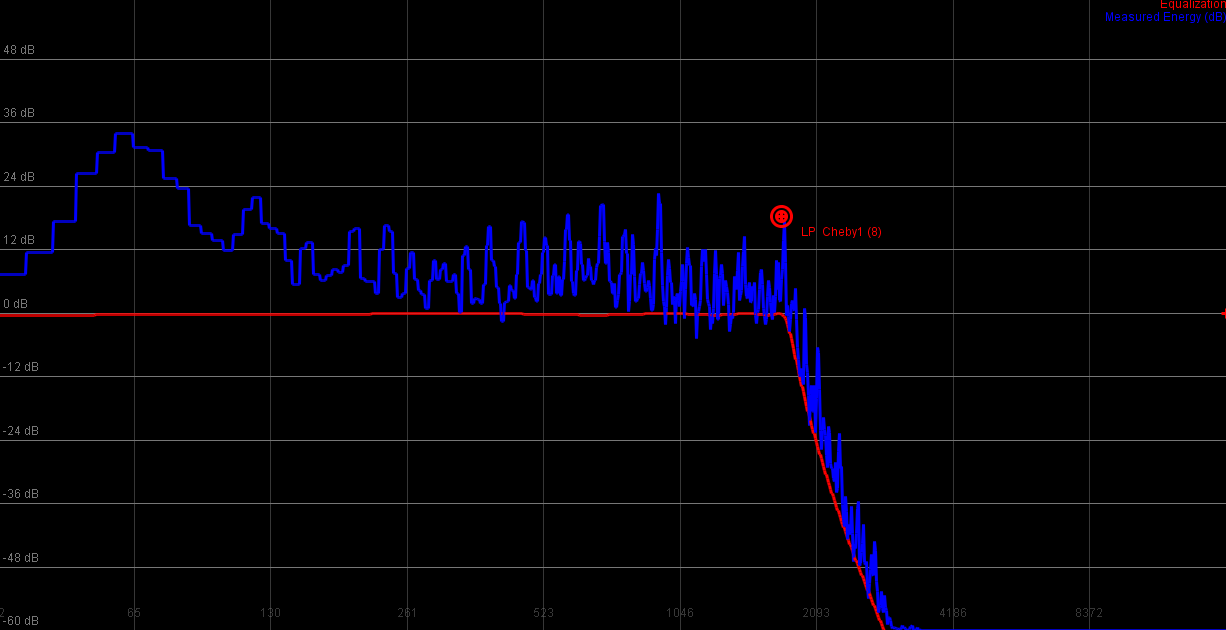
8th order highpass

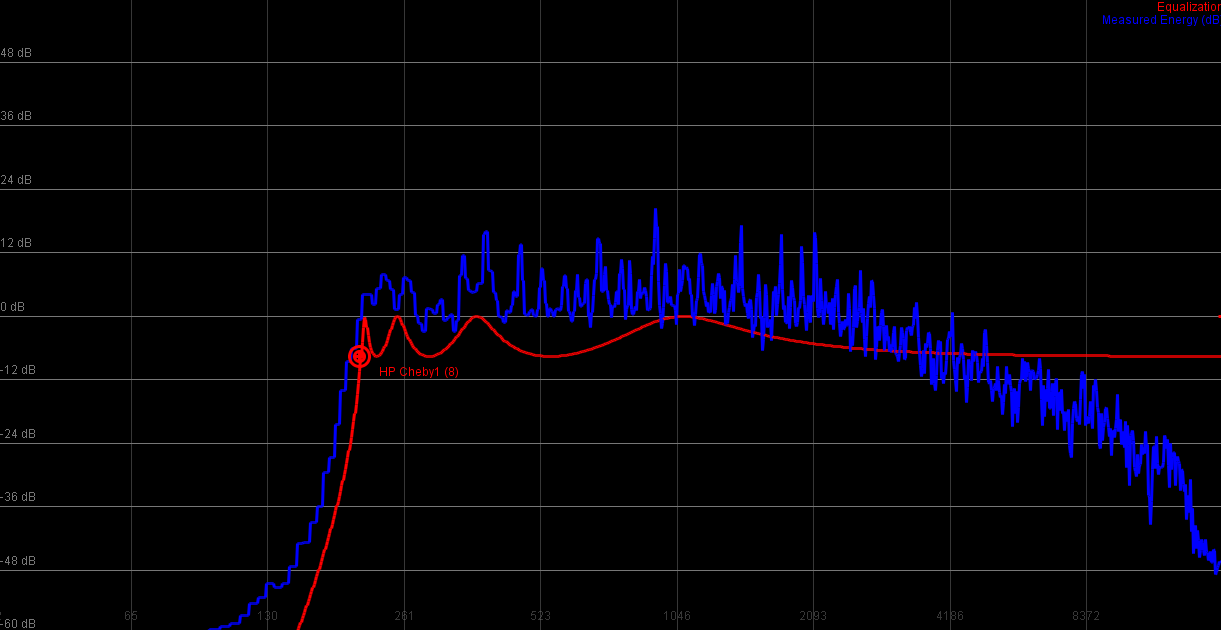
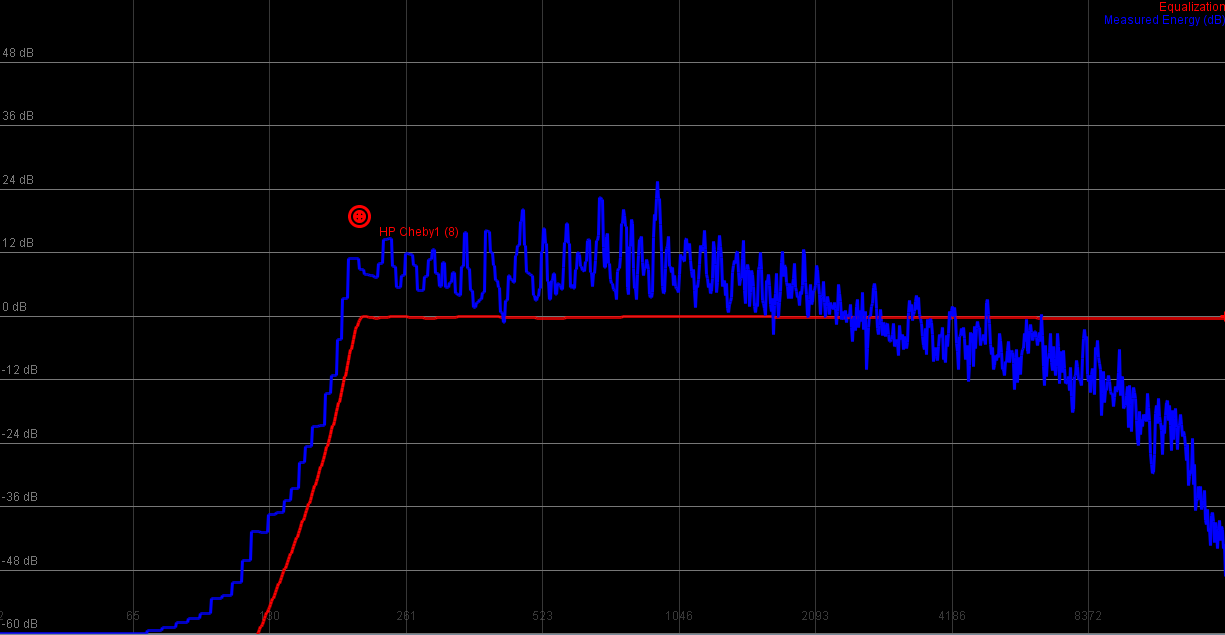
Chebyshev Type 2

The Chebyshev type 2 filter (one in which the transfer function was inverted by subtracting it from 1), moves the ripple to the stop band. Again, good effect filter, otherwise too complicated to deal with.

8th order lowpass

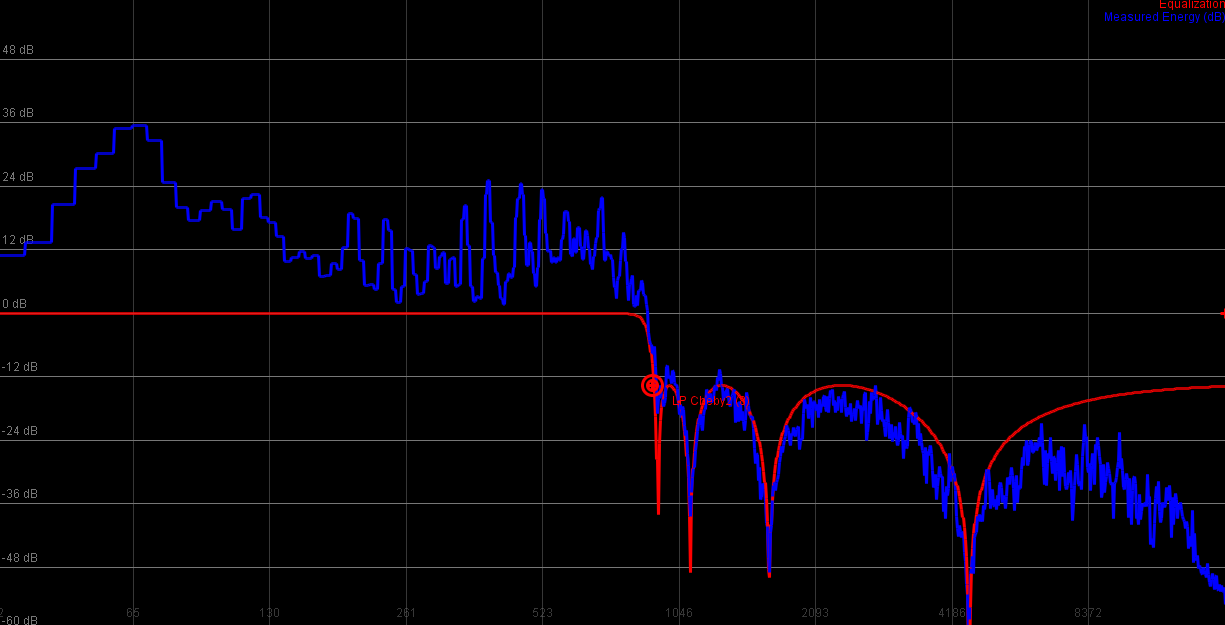
8th order highpass

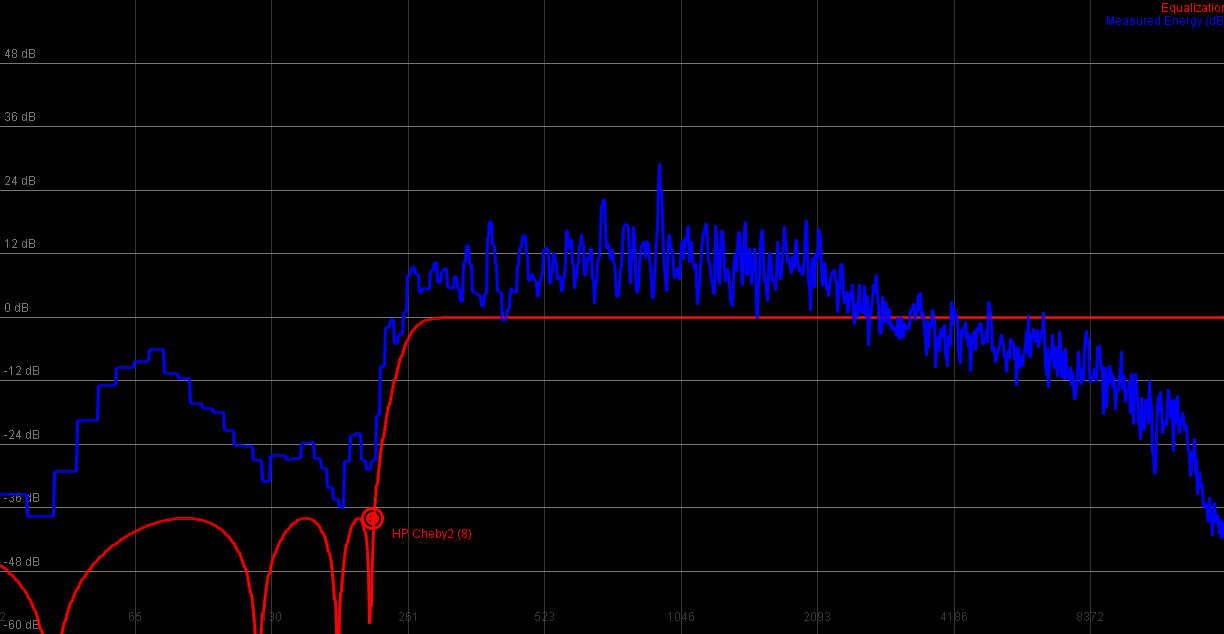
References

1.	On the theory of Filter Amplifiers S. Butterworth Experimental Wireless and the Wireless Engineer, vol. 7, pp. 536–541, 1930
2.	Crossovers Siegfried Linkwitz Linkwitz Lab http://www.linkwitzlab.com/crossovers.htm
3.	Butterworth band-pass filter Miller Puckette 3 March 2006 http://crca.ucsd.edu/~msp/techniques/v0.08/book-html/node141.html

http://werner.yellowcouch.org/
werner@yellowcouch.org