| Home | Papers | Reports | Projects | Code Fragments | Dissertations | Presentations | Posters | Proposals | Lectures given | Course notes |
|
Reinforcement Learning as a Routing Technique for Mobile Multi Agent SystemsWerner Van Belle1* - werner@yellowcouch.org, werner.van.belle@gmail.com Abstract : Nowadays, a number of mobile multi agent systems are designed and implemented at a variety of research labs. Most of these systems suffer from a major problem: location transparency. Most systems do not implement this, and the few of them which do are not robust towards changes in the network topology and/or absolutely imperformant in wide area networks. In this paper we present a naming scheme and a location transparent routing algorithm, based upon reinforced Q learning, which is robust and performant.
Keywords:
reinforcement learning, packet Routing, mobile Multi Agent Systems |
Table Of Contents
Introduction
It is remarkable how we are moving from client/server computing to a more distributed model of computation. In this new model we see considerably more peer to peer communication. It is in this context that we can situate mobile multi agents. A mobile multi agent is a process associated with a state, which is able to communicate with other agents and which is able to move from one location to another.
We are working in a distributed environment where agents can move at any time from one place to another. The nodes in this network are connected by means of a LAN or WAN. The delays between the different hosts can be high and the throughput can vary widely. In this large environment, agents in different sizes travel at an irregular basis.
While we were looking at all sorts of agent systems, it became clear to us that the major problem with the use of these mobile multi agent systems lies in the lack of good routing algorithms, which give us a location transparent naming and routing service. In almost all mobile multi agent systems, there is a lack of interest how one agent can reach another one, or to say it otherwise, how the agent system routes messages between agents. Most agent systems push this problem back to the programmer of the agents, who should send location-updates to communication partners. It is our view that such a solution is unacceptable because when one writes code for his agent, he doesn't want to write code to reach other agents. This is the same as having to say in smalltalk how one sends a message. While this can be useful sometimes, there should be a good standard way to deliver messages.
To solve the problem we have to look at two closely related subproblems. On one hand, we should be able to give an agent a name which can be used, independent of the agents' location. This problem is called the naming of agents. On the other hand we have to create an algorithm which is able to reach an agent by only using this name.
To solve these problems, we will modify an existing routing technique, called Q-routing [1] by adding the ability to move agents. But first of all, we introduce a new way to name agents. After that we introduce the basic solution without reinforcement learning and finally we explain how one can use reinforcement learning to make the algorithm more robust and fault tolerant.
Naming
When one wants to give a name to an agent in agent systems these days, one chooses an arbitrary one, and it will be automatically prefixed by the name of the machine it is on. For example, an agent name could be igwe8.vub.ac.be/hea. When the agent migrates its prefix is changed to the name of its new location. For example, after movement the agent may be named igwe134.vub.ac.be/hea
This way of assigning names is absolutely braindead because 1) It is possible that two agents, coming from different hosts, want to create the same name on the same machine. For example: it is clearly impossible that two agents igwe7.vub.ac.be/hea1 and igwe7.vub.ac.be/hea2, both residing at igwe7, but coming from different hosts, can create an agent with the same name igwe7.vub.ac.be/ho. And 2) when they get a free name there can be a nameclash when migrating to other machines. For example: their will be a nameclash when two hea-agents, igwe7.vub.ac.be/hea and igwe8.vub.ac.be/hea, move to the same machine because their prefix changes.
This problem is crudely solved in the Aglet Workbench [2] by means of algorithmical generated identifiers (read: numbers). The problem of conflicting name spaces is solved this way, but we are nevertheless unable to keep track of an agent, nor can we reach an agent to talk with.
Others anticipates this problem in a slightly different way. In Mole [3], agents join a communication group. While communicating in such a group an agent must not move. It it does, the communication session is considered broken.
The difficulty lies in the fact that an agents' name should not be changed when the agent migrates. What we need is a naming scheme and routing algorithm in which
- Every agent has a human readable name
- An agent can choose an arbitrary name for an agent it creates
- This name should be globally unique
- If we send a message to an agent, we should use this name, even after migration of the agent.
- Migration of an agent should have as less as possible performance impact on the sending of messages to the agent.
The solution we propose is to take the crossproduct of two name-creation schemes. We prefix every name with the name of the creation machine and the name of the owner machine. (that is the machine from which the agent originally came). For example: an hea-agent made at igwe8 will have the name igwe8.vub.ac.be/igwe8.vub.ac.be/hea and an hea-agent created at igwe7 will have the name igwe7.vub.ac.be/igwe7.vub.ac.be/hea. If both agents move to the same host, their names will not change. If they both create a new agent at their new location, the two newly created agents will carry the name igwe1.vub.ac.be/igwe8.vub.ac.be/ho and igwe1.vub.ac.be/igwe7.vub.ac.be/ho. As you can see, both ho-agents have the same creation-machine, but their owner machine differs.
Routing
Almost all agent systems we looked at [2, 3, 4] uses a form of source routing (either with or without caching) to reach their agents. This means that before we send a message, we first look up the position of our target and after that we sent the message (In the Aglet Workbench the path to follow is called an itinerary). The main problem here is that we, in our view, cannot update a central name server because of the massive number of updates and requests to the name server. Every time an agent moves an update is send (which should be propagated throughout the entire network), and every time a message is send there is a name-lookup.
Another form of message routing is hop by hop routing, which is often implemented as stubs. Every time an agent moves it leaves a stub behind which transparently forwards every message to the effective agent. The drawback of this method is its lossy performance. Every message sent has to go trough the entire forwarding chain, which gets longer and longer every time the agent moves.
We propose an agent sensitive routing, based upon hop by hop routing wherein we collapse name services and routing. If we send a message, the local router first checks to see if the agent-name is known to be local. If it is, the message is directly send to the agent. If the local running agent system doesn't know where to send the message to, it will use its forwarding router. That router will see what it can do with the message and if it doesn't know, it will send it to its forwarding router. Every time an agent x passes through a router, the routing table is changed to point to the new forwarding router for agent x.
A major start hypothesis in the above scheme is that every message can reach a specific host and that every router knows how to reach a specific destination. If there isn't any information available for the agent we want to reach, we can fall back to this structural geographical knowledge and send the message to the creation host (which is encoded in the name of the agent). The graph should be directed with clear distinction between forwarding routers (up in the tree), and subnets (down in the tree).
Despite the fact this algorithm works, it is practically useless. The
main problem with this style of routing is that we can only assign one
forwarding router to each router, which is not realistic and not fault
tolerant. If we should allow a second forwarding router, then only one
of both routers will know where an agent is. If the message is sent to
the wrong router it will not be delivered. In the following section we
will solve this by adding reinforcement learning to the routing
algorithm.
Reinforcement Learning
Reinforcement learning gives us a technique to program routers with reward and punishment, without the necessity to specify how an agent should be reached. The router has to develop a behaviour by means of trial and error interaction with its dynamic environment [5, 6].
In the field of reinforcement learning, we detect two major strategies. The first strategy is to search a space of policies to find a policy which acts optimal or nearly optimal in an environment. This way of working is mainly used in genetic algorithms (GA) or genetic programming (GP). A second strategy is the use of statistical techniques and dynamic programming to determine the usefulness of actions taken in different states of the environment. This is the method we have used to solve the routing problem.
First of all we have to note that we are not working with one global learning algorithm, but merely with a learning algorithm at each participating router, which interacts with other learning routers.
Normally a router is connected to its environment through perception and action (receive/send). By means of an estimated state of its environment, the algorithm creates a set of possible actions. From these actions one gets chosen and acted out. This results in a state change. The router is informed of this new state through a scalar reinforcement signal r. The goal is to select that router which in time returns the best cumulated reinforcement. This can be done by a systematic trial and error online training. To model this, we distinguish the following:
- A discrete set of possible environment states, S. These are the connected neighbour routers which can be used to forward a message to. A state exists of a set of agents which are available at the local machine and a set of queued messages.
- A discrete set of actions A. In this case, this is the migration of a message from one router to another.
- A reinforcement signal r which is given by the environment, in this case the neighbour-routers.
In the general case, we expect to have to deal with non deterministic environments, that is, environments in which the undertaken action at different positions in time results in different reinforcement signals. We encounter this non determinism in the migration of an agent, the change of the network topology or a change in the load of the network. A start hypothesis for reinforcement learning to work is that the environment may not change over time. Since this won't be so, we won't have convergence to an optimal result. Instead we will have a probably approximately correct algorithm.
Formal description
Sets & Transitions
First, we define the necessary environment states and actions.
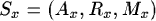
Sx is the set of possible states. The subscript x is a reference to the router which we're talking about. (This is needed because we are working with a number of routers and thus learning algorithms) The triplet contains a set Ax, which contains all agents available at that specific host. Rx refers to all neighbour hosts, while Mx contains all queued messages.
The only possible action is sending a message to another host. For clarity, we consider every router also as a host on which agents run to solve their quest.
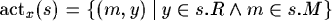
We don't need a set of goals because routers should run continuously.
Regarding the transistions, we have two possibilities: we can remove a message from the queue, or we can send a message to a neighbour host. The removal of a message is only needed if the target agent is on the local host.
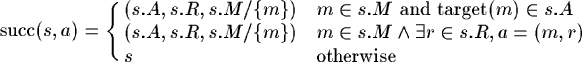
Algorithm
Qx(d, y) is the time estimated by node x, to send a packet P to agent d via neighbour node y (The time P spent in x queue has to be taken into account). The Q-learning algorithm is written as follows
- Select an action a in act_x(s)
- Enact a to reach succ(s, a) and receive a reward t
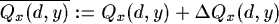
- Go to step 1
The packet routing policy answers the following question: to which neighbour router should we sent a packet to deliver it as fast as possible to its destination. The performance of such a policy is given by the total time to send a packet from A to B. It is clear that it is impossible to use an immediate training signal to enhance the policy under contemplation. However, by using only a local reinforcement signal, it is possible to change this estimation with a certain delay.
If P is effectively send to router y, y will send immediate an estimated time t, which P will need to reach d. If P remains g time units in x's queue and if the transmission between x and y is given by s, then we have the following change in estimated times:
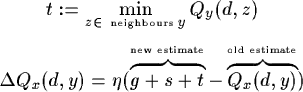
Initialisation
The initialisation of the tables is straightforward. Every agent which is known to be locally present is given estimation time 0, all the other agents are given an unexpected large estimation, but not infinity, because that leads to a division by zero in the calculation of new reinforcements.
Further, the Q-time of a forwarding router should be lower than the others, hereby reflecting the network topology. For example: Qx(d, y) is 50000 if y is not a forwarding router and nothing is know about d. Qx(d, y) is 25000 if y is a forwarding router and nothing special is known about d.
When bootstrapping a router, that router has to connect to its own forwarding routers and send its local routing information. After that, subparts of the network will connect to the newly booted router and send their routing tables. This is useful as a backup when a router looses its routing tables.
Creation and movement of agents
The creation of agents embraces a bit more than instantiating and binding the agent to a name. It is for example possible to create a new name which has previously been moved to another host.
As such, whenever we create a name we should remove the path which may already exist for the agent. This means that we should create a fake agent which goes to the position of the name we want to assign. From there the agent should travel back to the local machine and update the routing tables on its way back. (This is closely related to the termination of an agent. An agent should terminate on its creation machine.)
If an agent wants to move, it is moved by the routers just like a message would be send. By every hop we will change the estimation on the sending router to the transmission and queuing time between it and the forwarding router. The receiver router changes its estimation to 0.
Example
In this section we give an example for those who want to study the algorithm in detail. We describe the initialisation and interconnection of the routers. After that we describe how messages are send and how a router changes its estimations when agents migrate. At last we explain why cycles are no problem.
Situation
|
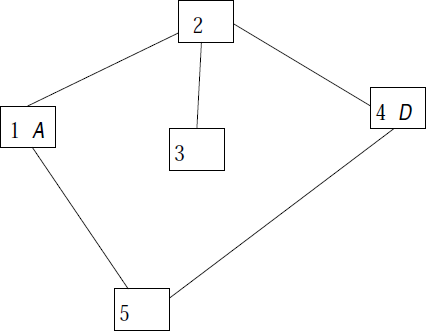
In the above figure, we see an interconnection between the hosts. Machine 1 is able to send messages to machine 2 and 5. Machine 2 can send messages to machines 1, 3 en 4 and so on. Machine 1 contains one agent A and machine 4 contains agent D.
The links between all the hosts can send a message in 0.01 secs. For the sake of simplicity, we consider a queuing delay of 0.001 secs.
Initialisation
The initialisation of the routers looks as follows (The use of wildcards in routing tables is a handy and necessary tool to restrain the size of the tables.)
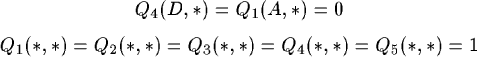
The first rule states that we can always reach agent A from host 1 in no time, independent of the host to which we send the message. This is normal because agent A is direct available at host 1. The same counts for agent D. The second rule states that for every other agent we estimate a large delivery time because we have absolutely no clue where the agent is.
Sending a message from A to D
Sending a message from agent A to agent D starts at host 1.
- First, we have to choose an action. We can forward the message to machine 2 or machine 5. We choose machine 2.
- Machine 2 sends back a reinforcement t.
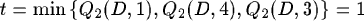
- To change the reinforcement on machine 1 we consider a learning rate of 0.75. This gives a Q1(D, 2) = 1.00825, which means that the estimated time to reach agent D via machine 2 is raised.
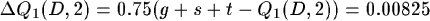
The second step in sending the message, is the forwarding of the message on router 2.
1. We have to choose an action again. We can choose machine 1, 3 or 4. We choose machine 4. In the subsection `cycles' we describe what would happen if we chose machine 1. 2. g = 0:01, s = 0:001 en t = 0 because machine 4 returns the best-guess to reach agent D. In this case is this 0 because he knows the position of agent D. 3. Q2(D, 4) = 1 + 0.75(0.011 - 1) = 0.25825 The routing tables after this step looks as follows: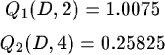
Sending a 2nd message from A to D
If we send a second message from A to D, using the same path, the certainty on machine one will increase. We encounter a backward propagation of reinforcements. Or, in other words, router 1 receives a delayed reward for sending to machine 2.
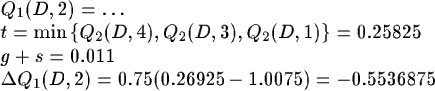
which gives a new estimation Q1(D, 2) = 0.4538125.
which gives a new estimation Q2(D, 4) = 0.0728125. We see a convergence to the transmition time between host 2 and 4.
Cycles
Cycles occur when a router thinks the agent is in its subnet and the subrouter thinks that the agent is higher in the tree. Despite being very nasty, cycles are no problem for this algorithm. The intuition is clear: the estimated time to reach a particular host increases with every rotation. At last, the routers will choose a different path. We illustrate this:Suppose that after sending the first message from 1 to 2, router 2 decides to send the message back to machine 1. The estimation of the delivery time will increase on both hosts. Let's have a look at machine 2. After sending the message back it gets a reinforcement t = 1 returned.
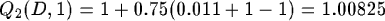
Migration of agent D to machine 5
If we move agent D to machine 5, the routing tables will change as follows:
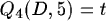whereby t is the transmition time between machine 4 en 5.
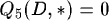
The major innovation with this way of routing is that the migration of agents does not require centralized position updates, instead we only have to update a table on every host the agents passes.
Conclusion
In this paper, we've presented two things. The first being a new naming scheme for mobile multi agents, which avoids name clashes. The second is a learning routing technique for mobile multi agent systems, which is robust towards changes in the network topology and which is performant. Alas, we do not guarantee ordered delivery. But this is no problem since other levels of abstraction may tackle this problem. A second, more serious problem, are the sizes of the routing tables. In the example, we've used wildcards to restrain the sizes of them. It is obvious that this is impossible if we work with scalar entities. A possible way out of this may be neural networks.
Bibliography
| 1. | Packet Routing in Dynamically Changing Networks: A Reinforcement Learning Approach Justin A. Boyan, Michael L.Littman Carnegie Mellon University, Cognitive Science Research Group (Bellcore) |
| 2. | Agent Transfer Protocol ATP/0.1 Draft Danny B. Lange IBM Tokyo Research Laboratory, 29 July 1996; aglets@yamato.ibm.co.jp http://www.trl.ibm.co.jp/aglets |
| 3. | Mole - Concepts of a Mobile Agent System Joachim Baumann, Fritz Hohl, K. Rothermel, M. Strasser Institut für Parallele und Verteilte Höchstleistungsrechner (IPVR) Fakultät Informatik, Stuttgart Augustus 1997 |
| 4. | The Caltech Infospheres Project Joseph R. Kiniry, K. Mani Chandy Technical report published by the Caltech Infosphere Group in 1997-1998 http://www.infospheres.caltech.edu/ |
| 5. | Agents and Reinforcement Learning: Making Software Agents do the right thing Satinder Singh, Peter Norvig, David Cohn Dr. Dobb's Journal, March 1997 |
| 6. | Reinforcement Learning: A Survey Leslie Pack Kaelbling, Michael L. Littman, Andrew W. Moore Brown University Providence, Carnegie Mellon University Journal of Artificial Intelligence Research 4 (1996) 237-285 |
| http://werner.yellowcouch.org/ werner@yellowcouch.org |  |