Estimating Invariant Principal Components Using Diagonal Regression results in the same projection as correlation PCA.

Werner Van Belle¹^* - werner@yellowcouch.org, werner.van.belle@gmail.com

1- Yellowcouch;

Abstract : In May 2016 I studied the working paper 'Estimating Invariant Principal Components Using Diagonal Regression' by Michael Leznik and Chris Tofallis from the Department of Management Systems The Business School University of Hertfordshire. The reason I was interested in this work is because they apparently found a different approach to the problem of PCA scale sensitivity than correlation PCA. In this brief note I explain how these two methods are the same.

Keywords: scale invariant pca, correlation pca, eigenvectors
Reference: Werner Van Belle; Estimating Invariant Principal Components Using Diagonal Regression results in the same projection as correlation PCA.; Statistics; YellowCouch; May 2016
Files: paper.pdf

Table Of Contents

Introduction
Scale Invariant PCA
Correlation PCA

SIPCA projection ~ CPCA projection
The principal axes
Conclusion

Introduction

In May 2016 I studied the working paper 'Estimating Invariant Principal Components Using Diagonal Regression' by Michael Leznik and Chris Tofallis from the Department of Management Systems The Business School University of Hertfordshire. The reason I was interested in this work is because they apparently found a different approach to the problem of PCA scale sensitivity than correlation PCA. In this brief note I explain how these two methods are the same. In this paper we deal with a dataset 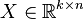which comprises k variables and n observations. We assume, without loss of generality, that the data is mean centered. Thus .

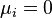Scale Invariant PCA

The authors go through a fairly complex argumention, proposing that a true regression should be estimated differently. They integrate a 'true regression' in a PCA analysis and find out that this is actually feasable. The resulting algorithm is to set up a moment matrix

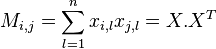
and a scaled variance matrix

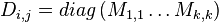
With this definition 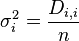. These two variables then participate in the general eigenvalue problem

Equation 1: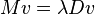

In line with their argumentation, the eigenvectors v and eigenvalues 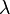present a scale invariant PCA, believed to be different from a correlation PCA.

To solve this general eigenvalue problem they define the substitution

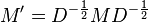
Now, at this point, the paper implies that 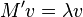is the same as 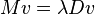. That is however incorrect. To correctly solve equation 1, an extra substitution

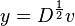
is necessary. Luckily, this error goes unnoticed in the examples because Matlab computes the eigenvectors correctly.

If we now write these two substitutions out, we get

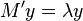
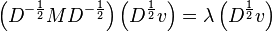
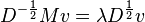
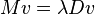
Thus by calculating the eigenvalues and eigenvectors of 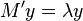we can obtain the eigenvalues and eigenvectors of the general eigenvalue problem. The eigenvalues are the same in both systems. The eigenvectors are related as 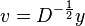. Or, stated differently, the values of the eigenvectors of M' have to be divided by the standard deviation of the respective variables.

Assume that the eigenvalues/vectors of M' are written as 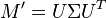, then the eigenvectors v of equation 1 are the columns of 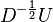. As a result, the SIPCA projection of the data is

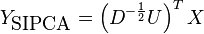
Correlation PCA

Now, let us focus on what a correlation PCA does. Obviously, it starts out from a correlation matrix (we still work on the mean centered data X)

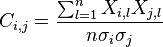
This is easier to write when we work with a normalized dataset X'

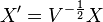
with V defined as a diagonal matrix containing the variances: 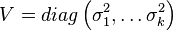. The correlation matrix can now be written as:

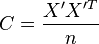
The eigenvalues and eigenvectors of C are computed using a singular value decomposition:

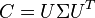
To project the dataset, we multiply 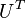with the normalized dataset:

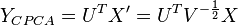
SIPCA projection ~ CPCA projection

To prove that both projections are the same, observe that the variance matrix V of section 2 is related to matrix D (section 1) as follows:

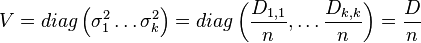
The correlation matrix C from section 2 is the same as the substitution M' in section 1. Namely

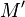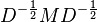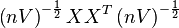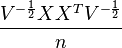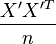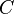Now, with M' equal to C, their eigenvalues and eigenvectors will be the same. Thus .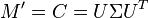

In section 2, the projected data is given as

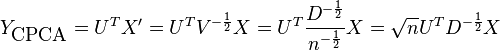
The projected data of the scale invariant PCA is:

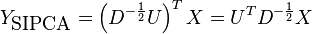
It is clear that

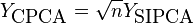
which in the context of principal component projection is the same. (It should maybe be noted that it might have made some sense to premultiply 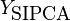with 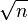, otherwise the SIPCA might very well be scale invariant but not invariant to the number of observations.)

The principal axes

Allthough the projected data is the same, one could argue that the eigenvectors still represent something different.

In a correlation PCA both the projection and the eigenvectors are scale invariant. The eigenvectors tell us along which axis the normalized data has most variance. For visualisation purposes, these vectors can be projected back to the original dataset by multiplying the eigenvector matrix with the standard deviations. Thus 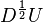provides us with the eigenvectors expressed at the scale of the original dataset.

With the scale invariant PCA, the situation is different. It provides only a scale invariant projection; one that is equivalent to the correlation PCA. Its eigenvectors on the other hand are scale sensitive (If we multiply variable i with a factor r, then we will find that the eigenvectors 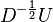will have row i divided by r). For visualisation purposes, the scale invariant eigenvectors make no sense whatsoever. That is because they tell us how the non-normalized data should be rotated and scaled to have the most variance along the first projected dimensions. Such matrices tends to have a large shearing factor, making it inappropriate to draw them as a basis in the original data set.

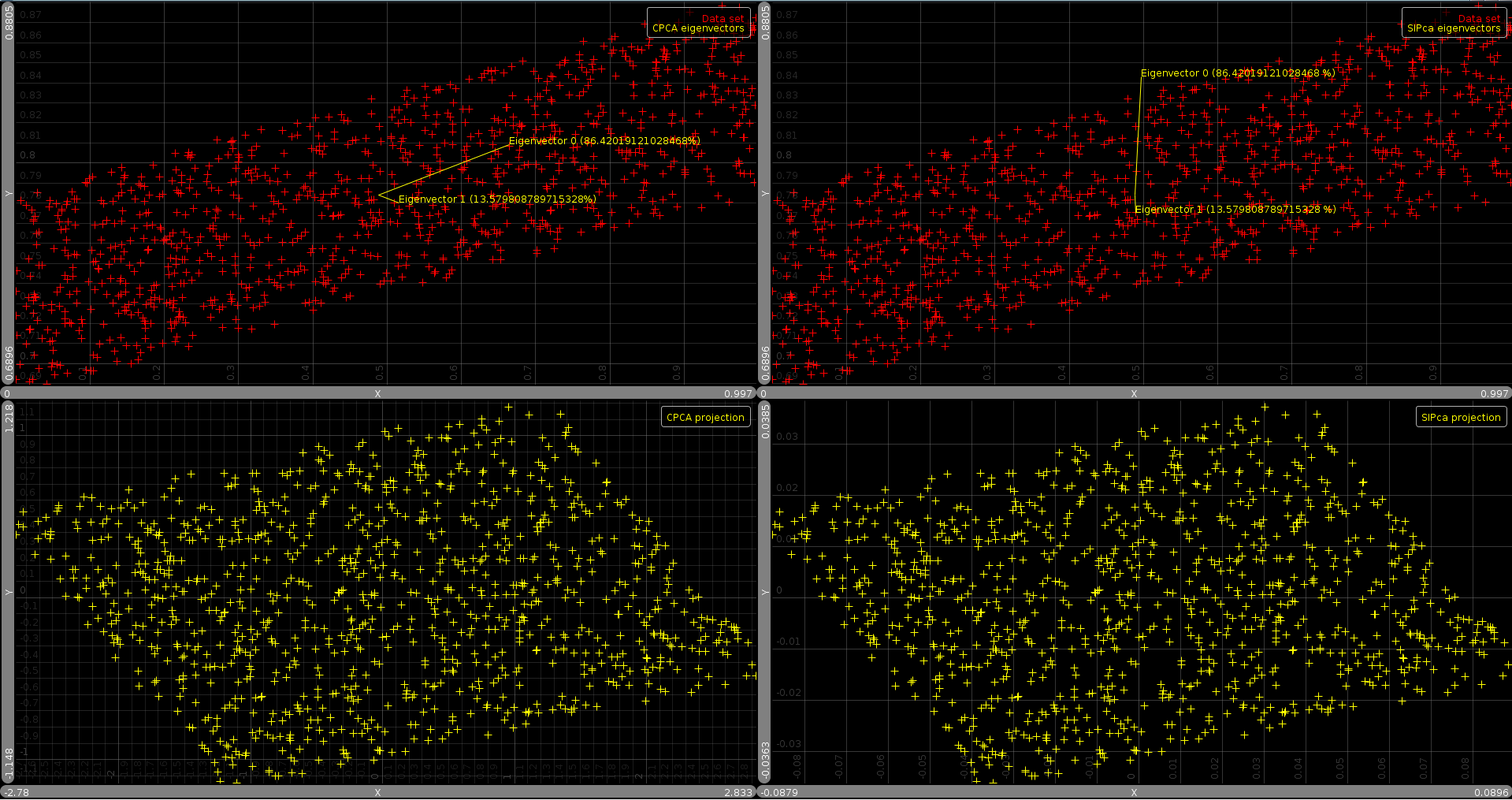
The above picture presents an example of the eigenvectors as provided by the two methods. The bottom plots show the projected data (Note that the projected SIPCA data is at a different scale than the CPCA data. With 1000 points it is 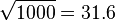times smaller).

Conclusion

We have shown that the scale invariant PCA as defined by Leznik and Tofallis results in the same projection as a correlation PCA. However, in contrast with a correlation PCA, the eigenvectors of the SIPCA are not scale invariant, nor do they represent anything that can be easily understood.

http://werner.yellowcouch.org/
werner@yellowcouch.org