| Home | Papers | Reports | Projects | Code Fragments | Dissertations | Presentations | Posters | Proposals | Lectures given | Course notes |
|
|
Stepwise Tempo Changes in BpmDjWerner Van Belle1* - werner@yellowcouch.org, werner.van.belle@gmail.com Abstract : kbpm-play provides an algorithm that automatically changes the play-rate from its current speed back to normal speed. A first version of the software relied on a linear change of pace, which turned out to be slightly wrong. In this short article we describe what went wrong and how to do it right.
Keywords:
tempo changes, psychoacoustics, preceived tempo change, bpmdj |
1 Defining Variables
We define a number of variables necessary to investigate the problem.
- [
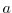 ] the current play speed of
the song, expressed in samples/second.
] the current play speed of
the song, expressed in samples/second. - [
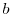 ] the target play-speed,
expressed in samples per second.
] the target play-speed,
expressed in samples per second.
- [
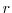 ] the sample rate of the
original soundtrack. In BpmDj this
is 44100 Hz.
] the sample rate of the
original soundtrack. In BpmDj this
is 44100 Hz.
- [
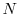 ] defines the number of steps
necessary to reach the final
speed
] defines the number of steps
necessary to reach the final
speed 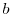
- [
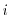 ] the current step. This
variable ranges from 0 (at which
moment the speed is supposed to be
] the current step. This
variable ranges from 0 (at which
moment the speed is supposed to be 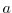 ) to
) to 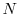 (at
which moment
the play-speed should be
(at
which moment
the play-speed should be 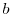 ).
).
- [
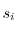 ] the playing
speed at step
] the playing
speed at step 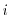 .
.
2 Linear change
A first straightforward approach to determine ![]() seems linear
interpolation, as follows
seems linear
interpolation, as follows
The main problem we observed with this approach was that the music
seemed to step up (or down) with an uneven pace. It did sound
wrong. A closer investigation reveals that simple interpolation will
lead to a non linear frequency change. To demonstrate this closer,
we will work with a song which has only one waveform: a pure sine
with frequency ![]() .
.
We
can now determine the frequency of that note at step ![]() (call
it
(call
it ![]() ) through multiplying it by
the current speed (
) through multiplying it by
the current speed (![]() )
and division by its normal speed (the sample-rate
)
and division by its normal speed (the sample-rate ![]() ).
).
Since human beings perceive frequencies in a non equally spaced manner,
we need to convert this frequency to a note in a (for this purpose)
equi-temporal scale. Rising one octave amounts to doubling of the
note frequency. If A4 is 440 Hz, then A5 will be 880 Hz and A3 is
220 Hz. Therefore, to map the frequency ![]() to its note number
we need to take
to its note number
we need to take ![]() (which will
yield the octave number) and
multiply it by 12 (to yield the note number). The perceived note at
step
(which will
yield the octave number) and
multiply it by 12 (to yield the note number). The perceived note at
step ![]() will be
will be
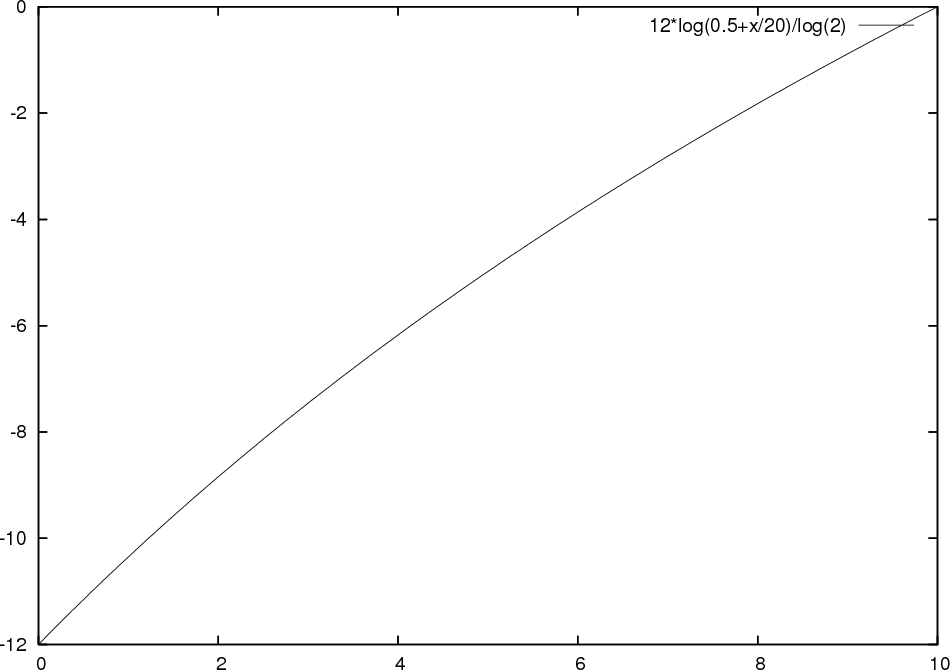
Clearly, we will hear a non-linear scale. To illustrate this, let
us assume that we would like to change the tempo of a song from half
the playing speed (![]() ) to its
normal playing speed (
) to its
normal playing speed (![]() )
in 10 steps. Figure 1 lays out the
transposition at
a given time step.
)
in 10 steps. Figure 1 lays out the
transposition at
a given time step.
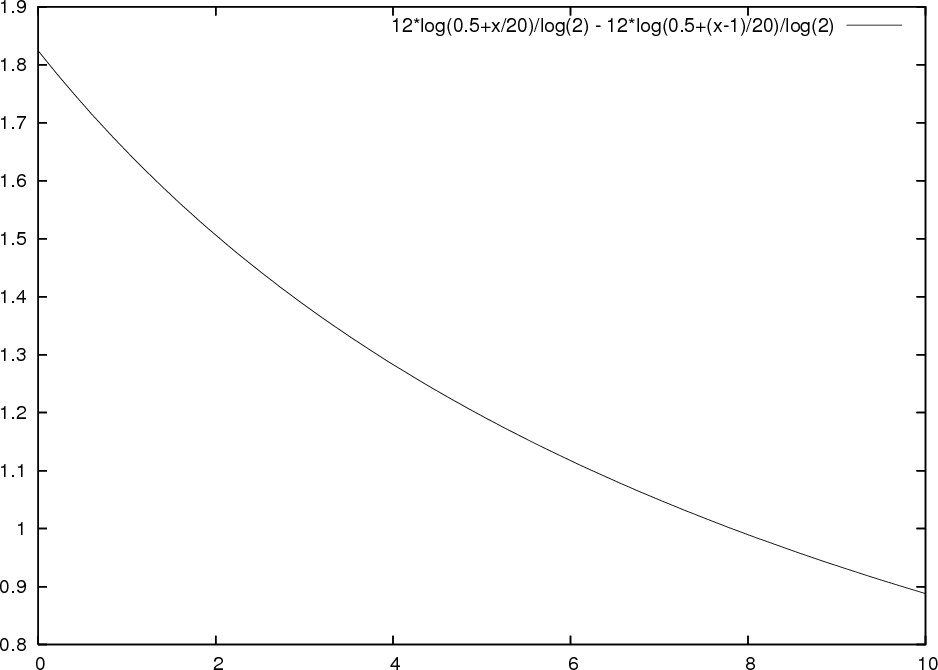
The slight bend we can observe does not look as much, but when looking at the local effect by measuring the transposition at every step then the problem becomes more obvious (see figure 2)
 |
3 Non linear change
To resolve this problem we must compensate for the logarithm and
express
our requirements on the note scale instead of the speed-scale. We
actually want the transposition at every step to be constant (called
![]() ). Formalized:
). Formalized:
According to 2 this becomes
![]() .
According to 1 this further gives
.
According to 1 this further gives
Merging various constant factors (12, ![]() and
and ![]() )
into
)
into ![]() gives
gives
and thus ![]() , in which
, in which ![]() will
be a constant itself.
will
be a constant itself.
In other words we need a constant multiplier for the playing speeds
instead of a constant difference. By induction we get ![]() ,
,
![]() ,
,
![]() which leads
to
which leads
to
We further know that ![]() and that
and that ![]() , so
, so
Isolating ![]() gives
gives
Practically, filling 4 into 3 gives
To calculate the logarithm using a specific base ![]() (10 or
(10 or ![]() for instance) use the following
for instance) use the following
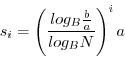
| http://werner.yellowcouch.org/ werner@yellowcouch.org |  |