|
|
| a=b=c=d=e=f=1 |
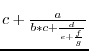
|
| a=d=2
b=c=-1 e=f=g=1 |
|
| a=b=c=d=e=g=i=1
h=-1 |
| O n l i n e P u b l i c a t i o n | C o m p u t e r S c i e n c e | Course Notes | http://werner.onlinux.be/ |
Werner Van
Belle
14 July 2006
e-mail: werner@onlinux.be
Abstract: These notes belong to the course 'Structuur en interpretatie van computerprogammas' as given at the Computer science Department, Vrije universiteit Brussel in 1994. The excercies themselve were create by Serge Demeyer and Karel Driesen (I believe). Some of the solutions I present here could be better, others are incomplete. Anyway, The most interesting part about these excercise are the environment diagrams that presented the ideas of lexical and dynamic scoping very well. I believe these were based on the book 'Structure and Interpreation of Computer Programs' as written By Abelson & Sussmann. The .PDF file includes figures as well.
Keywords: Course Notes
Structure of Computer Programs 1
Download: pdf
Files: LES1-1 (.html, .scm) | LES1-2 (.html, .scm) | LES1-3 (.html, .scm) | LES1-4 (.html, .scm) | LES1-E (.html, .scm) | LES2-1 (.html, .scm) | LES2-10 (.html, .scm) | LES2-11 (.html, .scm) | LES2-2 (.html, .scm) | LES2-3 (.html, .scm) | LES2-4 (.html, .scm) | LES2-5 (.html, .scm) | LES2-6 (.html, .scm) | LES2-7 (.html, .scm) | LES2-8 (.html, .scm) | LES2-9 (.html, .scm) | LES3-1 (.html, .scm) | LES3-2 (.html, .scm) | LES3-3 (.html, .scm) | LES3-4 (.html, .scm) | LES3-5 (.html, .scm) | LES3-6 (.html, .scm) | LES3-7 (.html, .scm) | LES3-8 (.html, .scm) | LES3-9 (.html, .scm) | LES4-1 (.html, .scm) | LES4-10 (.html, .scm) | LES4-2 (.html, .scm) | LES4-3 (.html, .scm) | LES4-4 (.html, .scm) | LES4-5 (.html, .scm) | LES4-6 (.html, .scm) | LES4-7 (.html, .scm) | LES4-8 (.html, .scm) | LES4-9 (.html, .scm) | LES4-T (.html, .scm) | LES5-1 (.html, .scm) | LES5-10 (.html, .scm) | LES5-2 (.html, .scm) | LES5-3 (.html, .scm) | LES5-4 (.html, .scm) | LES5-5 (.html, .scm) | LES5-6 (.html, .scm) | LES5-7 (.html, .scm) | LES5-8 (.html, .scm) | LES5-9 (.html, .scm) | LES5-E (.html, .scm) | LES6-1 (.html, .scm) | LES6-2 (.html, .scm) | LES6-3 (.html, .scm) | LES6-4 (.html, .scm) | LES6-5 (.html, .scm) | LES6-6 (.html, .scm) | LES6-7 (.html, .scm) | LES7-1 (.html, .scm) | LES7-2 (.html, .scm) | LES7-3 (.html, .scm) | LES7-4 (.html, .scm) | LES7-5 (.html, .scm) | LES7-6 (.html, .scm) | LES7-7 (.html, .scm) | LES7-8 (.html, .scm) | LES7-9 (.html, .scm) | LES7-E (.html, .scm) | LES9-1 (.html, .scm) | LES9-2 (.html, .scm) | LES9-3 (.html, .scm) | LES9-4 (.html, .scm) | LES9-5 (.html, .scm) | LES9-6 (.html, .scm) | LES9-7 (.html, .scm) | LES9-8 (.html, .scm) | LES10-1 (.html, .scm) | LES10-2 (.html, .scm) | LES10-3 (.html, .scm) | LES10-4 (.html, .scm) | LES10-5 (.html, .scm) | LES10-6 (.html, .scm) | LES10-7 (.html, .scm) | LES10-8 (.html, .scm) | LES11-1 (.html, .scm) | LES11-2 (.html, .scm) | LES11-3 (.html, .scm) | LES12-1 (.html, .scm) | LES12-2 (.html, .scm) | LES12-3 (.html, .scm) | LES12-4 (.html, .scm) | LES12-5 (.html, .scm)
Question:1.Schrijf volgende expressies in Scheme. Bedenk waardes voor de parameters zodat de eerste twee expressies 0 en de laatste 1 voorstellen. Identeer om de leesbaarheid te verhogen.
|
|
|||
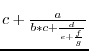 |
|
|
||
|
|
Question:
2. Voorspel voor elk van onderstaande expressies het resultaat indien ze in de gegeven volgorde geëvalueerd worden, leg de gevallen uit waarbij het misloopt. Teken het omgevingsdiagram voor zover het relevant is voor de evaluatie. Controleer je prognose daarna d.m.v een scheme vertolker.
Answer:
b) (* (+ 2 2) (5)) attempt to call a non procedural object
c) (* (+ (2 2) 5)) ""
d) (* (+ 2
2) 5) ""
e) (5 * 4) ""
f) 5 * 4 niet gedefinieerd object
g) (define 5*4 20) 5*4
h) 5*4 20
i) (5 * 2+2) 2*2 niet gedefinieerd
j) (5 * (2+2)) 2+2 is geen procedure
k) (5 * (2 + 2)) 2 is geen procedure
l) (5*2 + 2) 5*2 is geen procedure
m) (5*4 + 2) 20 is geen procedure
n) (5*(+ 2 2)) 5* is geen procedure
o) ((+ 2 3)) 5 is geen procedure
p) (/ 6 2) 3
q) / #<PROCEDURE />
r) (define $ /) $
s) (define / (* 2 3)) /
t) (/ 6 2) 6 is geen procedure
u) / 6
v) ($ 6 2) 3
w) $ #<PROCEDURE />
x) (* 2 /) 12
y) (define (double x) (+ x x)) #double
z) (double (double 5)) 20
A) (define (five) 5) #<PROCEDURE five>
B) (define four 4) four
C) four 4
D) five procedure
E) (four) call to non-procedural object
F) (five) 5
Answer:
(define (Sum-Sqr x y z)
(+ (sqr x)
(sqr y)
(sqr z)))
Answer:
(- (* 1.8 (+ 40 C)) 40))
Answer:
(/ (* basis hoogte) 2))
(define (OppervlakteRechthoek zijde1 zijde2)
(* zijde1 zijde2))
(define (OppervlakteVierkant Zijde)
(OppervlakteRechthoek Zijde Zijde))
(define (OppervlakteTrapezium GroteBasis KleineBasis, Hoogte)
(/ (* Hoogte
(+ GroteBasis
KleineBasis))
2))
(define (OppervlakteRuit diag1 diag2)
(OppervlakteDriehoek diag1 diag2))
(define (OppervlakteCirkel straal)
(* pi straal straal))
(define (OmtrekCirkel straal) (* 2 pi r))
(define (OppervlakteEllips straal1 straal2)
(* pi straal1 straal2))
Question:1. Definieer de procedure SIGN die een nummer als argument neemt en 1 teruggeeft als dat nummer positief is, -1 als het negatief is, en 0 als het gelijk is aan 0. Vb (Sign -5) ==> -1.
Answer:
(cond ((< x 0) -1)
((> x 0) 1)
(else 0)))
Answer:
(= (remainder y x) 0))
(define (LEAP-YEAR x)
(if (divides 4 x)
(if (divides 100 x)
(if (divides 400 x)
#t
#f)
#t)
#f))
(and (divides 4 x)
(or (not (divides 100 x))
(divides 400 x))))
Answer:
b) (define b (+ a 1)) b
c) (if (> a b) a b) 4
d) (+ 2 (if (> a b) a b)) 6
e) (* (cond ((> a b) a)
((< a b) b)
(else -1))
(+ a 1)) 16
f) ((if (< a b) + -) a b) 7
(MY-AND (< 1 2) (1)) (AND (< 1 2) (1))Answer:
(define (MY-AND e1 e2)
(if e1
(if e2
#t
#f)
#f))
(MY-AND (> 1 2) (1)) error
(MY-AND (< 1 2) (1)) error
(AND (> 1 2) (1)) #f
(AND (< 1 2) (1)) error
Question:5. Geef een expressie die zich voor een anologe MY-OR verschillend gedraagt dan wanneer je OR gebruikt.
Answer:
De gevraagde expressie zou als volgt kunnen luiden :
(OR (< 1 2) (1)) ;zal #t weergeven
(if (=y 0)
x
(/ x y)))
(define (foo-new-if x y)
(new-if (= y 0)
x
(/ x y)))
(cond (p e1)
(else e2)))
Question:7. Herdefinieer bovenstaande 'foo-new-if, zodat i.p.v. new-if een lambda functie gebruikt wordt.
Answer:
((lambda (p e1 e2)
(cond (p e1)
(else e2)))
(= y 0) x (/ x y)))
Answer:
(y (+ 1 x)))
(+ x y)
1 (+ 1 x))
Question:9. Vervang let in de vorige oefening door let*, en zet de uitdrukking om in een lambda-expressie. Leg uit waarom er deze keer niets misgaat.
Answer:
((lambda (y)
(+ x y))
(+ 1 x)))
1)
Question:10. Kun je onderstaande uitdrukking doen werken door let* te gebruiken ? Waarom (niet) ?
Answer:
(if (= n 0) 1 (* n (fac (- n 1)))))))
(fac 3))
((lambda (fac)
(fac 3))
(lambda (n)
(if (= n 0)
1
(* n (fac (- n 1))))))
Question:11. Wat is de output van (foo 1 2 3) ? En indien je alle let's door let* vervangt? Teken het environment diagram.
Answer:In de kolommen rechts staan steeds de waarden van a b & c. Als die regel onderstreept is wordt dit resultaat afgeprint.
(display a) (display " ")
(display b) (display " ")
(display c) (newline))
a b c
(define (foo a b c) 1 2 3
(print-abc a b c) 1 2 3
(let ((a 4) 4 2 3
(c 5) 4 2 5
(b c)) 4 3 5
(print-abc a b c) 4 3 5
(let ((b 6) 4 6 5
(c a)) 4 6 4
(print-abc a b c)) 4 6 4
(let ((a b) 3 3 5
(c a)) 3 3 4
(print-abc a b c))) 3 3 4
(print-abc a b c)) 1 2 3
4 3 5
4 6 4
3 3 4
1 2 3
Question:1. Definieer de vermenigvuldiging aan de hand van de optelling. Schrijf hiervoor de functie (MULT a b), die twee positieve getallen optelt.
a*1=a*0+a
a*2=a*1+a
a*3=a*2+a
Answer:
(define (MULTrec a b)
(if (= b 0)
0
(+ a (MULT a (- b 1)))))
(define (MULTiter a b)
(define (iter acc b)
(if (= b 0)
acc
(iter (+ acc a) (- b 1))))
(iter 0 b))
Answer:
(define (halve x) (/ x 2))
;dit is een recursieve versie
(define (fastMULTrec a b)
(cond ((= b 0) 0)
((even? b) (double (fastMULTrec a (halve b))))
(else (+ a (fastMULTrec a (- b 1))))))
(define (fastMULTiter a b)
(define (iter a b acc)
(cond ((= b 0) acc)
((even? b) (iter (double a) (halve b) acc))
(else (iter a (- b 1) (+ acc a)))))
(iter a b 0))
Answer:
(if (=n 0)
1
(+ (/ (factorial n))
(CALC-E (- n 1)))))
n x
1 1
2 1 + 2
3 1 + 2 + 3
4 1 + 2 + 3 + 4
(define (iter pos noemer acc)
(if (> pos n)
acc
(iter (+ 1 pos) (* noemer pos) (+ acc (/ 1 noemer )))))
(iter 1 1 0))
Answer:
(define (iter termnummer teller noemer acc)
(if (> termnummer n)
acc
(iter (+ termnummer 1)
(* teller x x) ;Hier twee vermenigvuldigingen
(- (* noemer (* termnummer 2)
(+ (* termnummer 2) 1)))
;Hierboven maar 2 vermenigvuldigingen. De *2 is
;geen vermenigvuldiging
(+ acc (/ teller noemer)))))
(iter 1 x 1 0))
Question:5. Geef de output van de uitdrukking (count1 4) en (count2 4) indien COUNT1 en COUNT2 als volgt gedefinieerd zijn :
Answer:
(cond ((= 0 x) (display x))
(else (display x)
(count1 (- x 1)))))
(define (count2 x)
(cond ((= 0 x) (display x))
(else (count2 (- x 1))
(display x))))
(count1 4) geeft als output 43210
(count2 4) geeft als output 01234
Answer:
(define (iter e)
(if (> (expt b e) n)
e
(iter (+ e 1))))
(iter 0))
Answer:
(cond ((= getal 0) #f)
((= getal 1) #t)
(else (even2? (- getal 1)))))
(define (even2? getal)
(cond ((= getal 1) #f)
((= getal 0) #t)
(else (odd2? (- getal 1)))))
= WEIRD(x/2) als x even is
= WEIRD (3*x+1) else
Answer:
(define (iter x count)
(cond ((= x 1) count)
((even? x) (iter (/ x 2) (+ count 1)))
(else (iter (+ (* 3 x) 1) (+ count 1)))))
(iter x 1))
Answer:
(define (iter b c)
(if (= b 0)
c
(iter (- b 1) (+ c 1))))
(iter b 1))
(define (fastmult a b)
(define (iter a b c)
(cond ((= b 0) c)
((even? b) (iter a (halve b) (+ c 1)))
(else (iter a (- b 1) (+ c 1)))))
(iter a b 1))
Question:Test : Schrijf een procedure (DISPLAY-AS-BINARY N), die een positief geheel getal N neemt, en dit in binaire vorm afdrukt. De meest rechtse bit is 1 als het getal oneven is, 0 als het getal even is. Voor de tweede bit van rechts deel je het getal door 2 (met de functie (QUOTIENT n1 n2) die het geheel equivalent is van (/ n1 n2)), en je doet dezelfde test. Voor de derde bit van rechts deel je het vorige quotiënt door 2 enz. Je mag een recursief proces genereren.
Answer:
(define (BINrec X)
(cond ((= X 0) (display "0"))
;iedereen zet onderstaande test erbij, maar deze
;hoeft niet
;((= X 1) (display "1"))
((even? X) (BINrec (quotient X 2)) (display "0"))
(else (BINrec (quotient x 2)) (display "1"))))
(binrec x)
(newline))
Maak gebruik van de sum-procedure (p.54)
Answer:
(define (iter acc p)
(if (> p b)
acc
(iter (+ acc (term p)) (next p))))
(iter 0 a))
(define (simp-int f a b n)
(let* ((h (/ (- b a) n))
(y (lambda (k)
(f (+ a (* k h)))))
(term
(lambda (k)
(cond ((= k 0) (f a))
((= k n) (f b))
((even? k) (* 2 (y k)))
(else (* 4 (y k))))))
(next (lambda (x) (+ x 1))))
(/ (* h (sum term 0 next n)) 3)))
Answer:
(define (iter pos acc)
(if (> pos b)
acc
(iter (next pos) (* acc (factor pos)))))
(iter a 1))
(define (factorial n)
(product (lambda (x) x) 1 (lambda (x) (+ x 1)) n))
Answer:
(define (iter pos acc)
(if (> pos b)
acc
(iter (next pos) (combiner acc (term pos)))))
(iter a null-value))
(define (product factor a next b)
(accumulate * 1 factor a next b))
(define (sum term a next b)
(accumulate + 0 term a next b))
Answer:
;de parameter filter bepaalt welke termen wegvallen
(define (iter pos acc)
(cond ((> pos b) acc)
((filter pos) (iter (next pos) acc))
(else (iter (next pos) (combiner acc (term pos)))))
(iter a null-value))
(define (product-gcd n)
(filter-accumulate
(lambda (i) (<> (gcd i n) 1))
*
1
(lambda (x) x)
1
(lambda (x) (+ x 1))
n))
Answer:
(accumulate
max ;combiner
(f a) ;null-value
(lambda (x) x) ;term
a ;a
(lambda (x) (+ x 1)) ;next
b)) ;b
Answer:
(accumulate
+ ;combiner
0 ;null-value
(lambda (n)
(/ 1 (factorial n))) ;term
0 ;a
(lambda (n) (+ n 1)) ;next
n)) ;b
(define (calc-sin x n)
(accumulate
+ ;combiner
0 ;null-value
(lambda (n)
(/ (expt x (+ (* n 2) 1))
(factorial (+ (* n 2) 1)))) ;term
0 ;a
(lambda (n) (+ n 1)) ;next
n)) ;b
Question:7. Het fixed-point van een functie f is het getal x waarvoor geldt f(x)=x. Voor sommige functies kan dit fixed-point gevonden worden door te beginnen met een willekeurige waarde x en de functie f herhaaldelijk toe te passen, f(x), f(f(x)), f(f(f(x))),... tot de waarde satbiel is. Schrijf de procedure (FIXED-POINT f x).
Answer:
(define (iter oude nieuwe)
(if (< (abs (- waarde oude)) 0.01)
nieuwe
(iter nieuwe (f nieuwe))))
(iter x (f x)))
Answer:
(f) (define f (lambda () 5))
(f 3) (define f (lambda (x) 5))
((f)) (define f
(lambda ()
(lambda () 5)))
(((f)) 3) (define f
(lambda ()
(lambda ()
(lambda (x) 5))))
Answer:
(lambda (x) (+ (* a (sqr x)) (* b x) c)))
(define VKV1 (make-vkv 3 5 1))
Answer:
(define (calc-n-maal x)
(define (iter nogtegaan result)
(if (= nogtegaan 0)
result
(iter (- nogtegaan 1) (f result))))
(iter n x))
calc-n-maal)
Question:1. Geef de box-en pointer representatie en de print-representatie van de onderstaande expressies.
Answer:
(1 2)
(cons 1 (list 2))
(1 2)
(cons 1 (cons 2 '()))
(1 2)
(list (list 1 2) (list 3 4))
((1 2) (3 4))
(list 1 2 (cons 3 (cons 4 5)))
(1 2 (3 4 . 5))
Answer:
(cond ((null? l) (error "kan niet"))
((null? (cdr l)) (car l))
(else (LAST (cdr l)))))
Answer:
(define (voorlaatste eindigtop)
(define (iter lst)
(if (eq? (cdr lst) eindigtop)
lst
(iter (cdr lst))))
(iter lst))
(define (iter newl lastlst)
(cond ((eq? lastlst lst) newl)
(else
(let ((newlast (voorlaatste lastlst)))
(iter (cons (car newlast) newl) newlast)))))
(if (null? lst)
(list el)
(let ((startlast (voorlaatste '())))
(iter (list (car startlast) el) startlast))))
Question:4. Schrijf de procedure (REVERSE l) die een lijst teruggeeft met dezelfde elementen als l maar in de omgekeerde volgorde. Maak 2 versies : één die een recursief proces genereert en één die een iteratief proces genereert. Denk eens na over de performantie.
Answer:
(define (iter l acc)
(if (null? l)
acc
(iter (cdr l) (cons (car l) acc))))
(iter l '()))
Answer:
(cond ((null? l) '())
((eq? (car l) e1) (cons e2 (change e1 e2 (cdr l))))
(else (cons (car l) (change e1 e2 (cdr l))))))
Answer:
(if (or (null? l1) (null? l2))
(eq? l1 l2)
(and (eq? (car l1) (car l2))
(equal? (cdr l1) (cdr l2)))))
Answer:
(list (list 'george)) ;((george))
(cdr '((x1 x2) (y1 y2)) ;((y1 y2))
(cadr '((x1 x2) (y1 y2)) ;(y1 y2)
(atom? (car '(a short list))) ;#t
(memq 'red '((red shoes) (blue socks)) ;#f
(memq 'red '(red shoes blue socks)) ;#t
(car ''abracadabra) ;quote
(cdddr '(this list contains '(a quote))) ;(quote (a quote))
(define q '(cons +))
(define r (list 'cons '+))
Answer:
((cadr p) 3 4) ;7
((car r) 3 4) ;'cons is geen procedure
((cadr q) 3 4) ;'+ is is geen procedure
Dit is raar want de lijst '(5 6 7) kan nadien wel met de nummers werken. Dit wil dus ook zeggen dat nummers in scheme niet bestaan maar wel cijferketens(strings). Een expressie zoals (+ '2 '4) zal als resultaat dus 6 geven (GETEST !!!). Nu nog een test plegen met de reële getallen. En deze schoppen alles overhoop. Die werkt hetzelfde als de gehele getallen maar hij blijft binnen de 10 cijfers...
Question:9. Schrijf een procedure mapcar, die twee parameters aanvaardt, een functie f en een lijst l. Het resultaat van mapcar zal een nieuwe lijst zijn, waarin de respectievelijke resultaten van de oproep van f met het overeenkomstige element uit l.
vb : (mapcar 1+ '(1 2 3 4)) ==> (2 3 4 5)
(mapcar square '(1 2 3 4)) ==> (1 4 9 16)
Answer:
(if (null? l)
'()
(cons (f (car l)) (mapcar f (cdr l)))))
(lambda (m) (m x y))
(define (car z)
(z (lambda (p q) p)))
Answer:
(z (lambda (p q) q)))
Question:Toegift : (ex-examenvraag) De procedure (SUM-lists l1 l2) heeft als argumenten 2 lijsten met getallen, en geeft een lijst terug met de sommen van de overeenkomstige elementen van de input-lijsten.
Vb : (Sum-lists '(1 2 3 4) '(5 6 7)) --> (6 8 10 4)
Merk op dat de 2 input-lijsten niet dezelfde lengte hoeven te hebben. In dit geval worden de resterende elementen van de langste lijst overgenomen. Schrijf een recursieve versie en een iteratieve versie.
Answer:Laten we maar van start gaan : ik heb twee recursieve versies geschreven, beide met een verschillende performantie (denk ik toch)
(cond ((null? l1) l2)
((null? l2) l1)
(else (append (list (+ (car l1) (car l2))) (Sum-list (cdr l1) (cdr l2))))))
(define (Sum-list2 l1 l2)
(cond ((null? l1)
(if (null? l2)
'()
(cons (car l2) (Sum-list2 '() (cdr l2)))))
((null? l2)
(cons (car l1) (Sum-List2 (cdr l1) '())))
(else (cons (+ (car l1) (car l2)) (Sum-list2 (cdr l1) (cdr l2))))))
(define (Sum-list3 l1 l2)
(define (iter result l1 l2)
(cond ((null? l1) (append result l2))
((null? l2) (append result l1))
(else (iter (append result (list (+ (car l1) (car l2))))
(cdr l1)
(cdr l2)))))
(iter '() l1 l2))
Question:1. Definieer een datastruktuur om een lijnstuk voor te stellen door middel van het start-en eindpunt van het lijnstuk. Schrijf hiervoor de constructor MAKE-SEGMENT en de selectoren START-POINT en END-POINT. Definieer een punt door middel van zijn x en y coordinaten. Schrijf de nodige constructor en selectoren. Schrijf de procedure MIDPOINT die het midden van een segment teruggeeft.
Answer:
eerst een definitie van de interface
een constructor make-segment
(define (endpoint segment) ...
de constructor
(define (ordinaat point)...
(define (make-point x y)
(cons x y))
(define (abcis point)
(car point))
(define (ordinaat point)
(cdr point))
(define (make-segment start end)
(cons start end))
(define (startpoint seg)
(car seg))
(define (endpoint seg)
(cdr seg))
eerst definieren van een hulpprocedure
(define (mid getal1 getal2)
(+ (getal1 (/ (- getal2 getal1) 2))))
(define (midpoint seg)
(make-point
(mid (abcis (startpoint seg))
(abcis (endpoint seg)))
(mid (ordinaat (startpoint seg))
(ordinaat (endpoint seg)))))
Answer:
samenvatting van constructors en selectors die nodig zijn :
(coordinate nummer wvect)
nummer loopt van 1 tot n
(dimension wvect)
coordinatenlijst)
(define (coordinate nummer wvect)
(define (getelement pos lst)
(if (= pos 1)
(car lst)
(getelement (- pos 1) (cdr lst))))
(if (or (< nummer 1) (> nummer (dimension wvect)))
(error "coordinate error...")
(getelement nummer wvect)))
(define (dimension wvect)
(define (iter acc lst)
(if (null? lst)
acc
(iter (1+ acc) (cdr lst))))
(iter 0 wvect))
(list->vector coordinatenlijst))
(define (dimension2 wvect)
(vector-length wvect))
(define (coordinate2 nummer wvect)
(if (or (< nummer 1) (> nummer (dimension2 wvect)))
(error "coordinate-error")
(vector-ref wvect (- nummer 1))))
Answer:
De interface
(v- wvect1 wvect2)
(v. wvect1 wvect2)
(define (same-dimension wvect1 wvect2)
(= (dimension wvect1) (dimension wvect2)))
(define (coordinatenlijst)
(define (iter coordinatenummer acclst)
(if (= coordinatenummer 0)
acclst
(iter
(- coordinatenummer 1)
(cons (combiner
(coordinate coordinatenummer wvect1)
(coordinate coordinatenummer wvect2))
acclst))))
(iter (dimension wvect1) '()))
(if (same-dimension wvect1 wvect2)
(make-w-vector (coordinatenlijst))
(error "verschillende dimensie")))
(define (v+ wvect1 wvect2)
(aux + wvect1 wvect2))
(define (v- wvect1 wvect2)
(aux - wvect1 wvect2))
(define (v. wvect1 wvect2)
(aux * wvect1 wvect2))
Question:4. Vectoren zijn ook punten in de n-dimensionale ruimte. Definieer de operaties uit oefening 1 (2de deel) aan de hand van de wiskundige vectoren uit oefning 2.
Answer:
(make-w-vector (list x y)))
(define (abcis point)
(coordinate 1 point))
(define (ordinaat point)
(coordinate 2 point))
Question:5. Definieer wiskundige veeltermen in één onbekende. Schrijf hiervoor de constructor MAKE-POLYNOME en de selectoren COEFFICIENT en ORDER. Gebruik de vectoren uit oefening 2 als implementatie.
Answer:
(list->vector coordinatenlijst))
(define (order pol)
(- (vector-length pol) 1))
(define (coefficient nummer pol)
;het nummer van de coefficient komt overeen met het nummer van de macht
;voor de variabele...
(let ((o (order pol)))
(if (or (< nummer 0) (> nummer o))
0
(vector-ref pol (- o nummer)))))
Answer:Om de optelling, aftrekking en dergelijke te definieren voel ik me geroepen een procedure te schrijven die een nieuwe polynoom ontwerpt door telkens de nieuwe coefficient op te vragen... De combiner neemt als parameter het coefficientnummer het resultaat van combiner moet de nieuwe coefficient zijn...
(define (iter coefnum acc)
(if (> coefnum to)
acc
(iter (1+ coefnum) (cons (combiner coefnum ) acc))))
(make-polynome (iter 0 '())))
(define (combine f pol1 pol2)
(define (combiner coefnum)
(f (coefficient coefnum pol1) (coefficient coefnum pol2)))
(aux combiner (max (order pol1) (order pol2))))
(define (+pol pol1 pol2)
(combine + pol1 pol2))
(define (-pol pol1 pol2)
(combine - pol1 pol2))
(define (*pol scalair pol)
(define (combiner coefnum)
(* scalair (coefficient coefnum pol)))
(aux combiner (order pol)))
Answer:
Normaal worden
![]() vermenigvuldigingen
gebruikt,
hieronder staat de oplossing in n=order vermenigvuldigingen :
vermenigvuldigingen
gebruikt,
hieronder staat de oplossing in n=order vermenigvuldigingen :
(define (iter coefnum acc)
(if (= coefnum 0)
(+ acc (coefficient 0 pol))
(iter (- coefnum 1) (* (+ (coefficient coefnum pol) acc) x))))
(iter (order pol) 0))
Question:1. Definieer de procedure (FRINGE l) die een lijst teruggeeft met alle atomen van de lijst l.
vb (fringe '((1) (((((2))))) ( 3 (4 5) ((6) ((((7)))))))) ==> (1 2 3 4 5 6 7)
Answer:
(cond ((null? l) '())
((pair? l) (append (fringe (car l)) (fringe (cdr l))))
(else (list l))))
Answer:
(if (null? l)
'()
(append (f (car l)) (map-cdr f (cdr l)))))
(define (remove-all e l)
(define (f key)
(if (eq? key e)
'()
(list key)))
(map-cdr f l))
Question:3. Definieer de procedure (UN-FRINGE l) die een platte lijst als argument neemt en een lijst teruggeeft die, net als al haar sublijsten, maximaal 2 elementen telt en terug l geeft als jer er fringe op loslaat. (OPM : Vermits verschillende lijsten hetzelfde resultaat kunnen opleveren met FRINGE, is het resultaat van UNFRINGE niet eenduidig bepaald)
vb: (un-fringe '(1 2 3 4 5 6 7 8 9))
==> ((((1 2) (3 4)) ((5 6) (7 8))) 9)
of ==> (1 (2 (3 (4 (5 (6 (7 (8 9))))))))
of ==> ((1 2) ((3 4) ((5 6) ((7 8 (9))))))
Answer:
(cond ((null? l) '())
(else (cons (car l) (list (un-fringe (cdr l)))))))
Answer:
(define (display-cons cns)
(display-list (car cns))
(cond ((null? (cdr cns)) #f)
((pair? (cdr cns))
(display " ")
(display-cons (cdr cns)))
(else
(display " . ")
(display (cdr cns)))))
(cond ((null? l) (display "()"))
((pair? l)
(display "(")
(display-cons l)
(display ")"))
(else (display l))))
'((a b) ((b c) ((c dt) ((p l) (l))))) ==>#t
(same-structure? '((1 2) ((3 4) ((5 6) ((7 8) (9)))))
'((((1 2) (3 4)) ((5 6) (7 8))) 9)) ==>#f
Answer:
(define (same-struct l1 l2)
(cond ((and (atom? l1)
(atom? l2)) #t)
((and (pair? l1)
(pair? l2)) (and (same-struct (car l1)
(car l2))
(same-struct (cdr l1)
(cdr l2))))
(else #f)))
vb : (DEEP-COMBINE-OVER-LIST + 0 '((((1 2) (3 4)) ((5 6) (7 8))) 9)) ==>45
Answer:
(cond ((null? l) null-value)
((pair? l)
(combiner (deep-combine-over-list combiner null-value
(car l))
(deep-combine-over-list combiner null-value
(cdr l))))
(else l)))
'((((1 . 2) (3 4)) ((5 6) (7 8))) . 9))
==> ((((1 . 4) (9 16)) ((25 36) (49 64))) . 81)
Answer:
(define (deep-map-over-atoms f l)
(cond ((null? l) '())
((pair? l)
(cons (deep-map-over-atoms f (car l))
(deep-map-over-atoms f (cdr l))))
(else (f l))))
(DEEP-CHANGE e1 e2 l) : geeft een lijst terug met dezelfde struktuur maar alle atomen e1 verandert in e2.
(DEEP-ATOM-MEMBER? e l) : kijkt of een atoom ergens in een geneste lijst voorkomt.
(COUNT-ATOMS l) : telt het aantal atomen in een (ev. geneste) lijst.
Answer:
(deep-map-over-atoms
(lambda (x)
(if (eq? e1 x)
e2
x))
l))
(define (deep-atom-member? e l)
(deep-combine-over-list
(eval 'or)
#f
(deep-map-over-atoms
(lambda (x)
(eq? x e))
l)))
(define (count-atoms l)
(deep-combine-over-list
+
0
(deep-map-over-atoms
(lambda (x) 1)
l)))
(*) kun je ook een DISPLAY-LIST schrijven aan de hand van TREE-ACCUMULATE ?
Answer:
(cond ((null? tree) null-value)
((pair? tree)
(combiner
(tree-accumulate (car tree) term combiner
null-value)
(tree-accumulate (cdr tree) term combiner
null-value)))
(else (term tree))))
(define (fringe l)
(tree-accumulate l list append '()))
(define (deep-combine-over-list combiner null-value l)
(tree-accumulate l id combiner null-value))
(define (deep-map-over-atoms f l)
(tree-accumulate l f cons '())
Question:Toegift : Een mobiel (zo'n ding dat je aan het plafond hangt en dat met de tocht beweegt), is ofwel een dom gewicht (getal), ofwel een koppel van twee armen, die elk een bepaalde lengte hebben, en waaraan weer een mobiel hangt. Je kunt er een construeren door (MAKE-MOBILE length1 weight1 length2 weight2), waarbij weight1 en weight2 ofwel getallen zijn (gewichten), ofwel meer mobielen. Definieer deze procedure en de corresponderende selectoren.
Definieer (MOBILE-WEIGHT m), die het totaal gewicht van het mobiel teruggeeft (het gewicht van de takken is verwaarlossbaar).
Een mobiel is in evenwicht wanneer het gewicht van tak1 maal de lengte van tek1 gelijk is aan het gewicht van tak2 maal de lengte van tak2, en wanneer deze conditie geldt voor alle sub-mobielen. definieer het predicaat (BALANCED? m), dat zegt of mobiel m gebalanceerd is.
Answer:
De Maniakale Mobiel
constructor
(rechterlengte mobiel)
(rechterhangsel mobiel)
(linkerhangsel mobiel)
(define (make-mobile l1 w1 l2 w2)
(cons (cons l1 w1)
(cons l2 w2)))
(define (linkerlengte mobiel)
;veiliger is hier een foutcontrole te steken, maar dat is
;niet gevraagd
(caar mobiel))
(define (rechterlengte mobiel)
(cadr mobiel))
(define (linkerhangsel mobiel)
(cdar mobiel))
(define (rechterhangsel mobiel)
(cddr mobiel))
(define (mobiel? mobiel)
(if (pair? mobiel)
#t
#f))
(if (mobiel? mobiel)
;als men een ECHTE mobiel vast heeft dan telt men de gewichten van de
;linkermobiel op bij de gewichten van de rechtermobiel...
(+ (mobile-weight (linkerhangsel mobiel))
(mobile-weight (rechterhangsel mobiel)))
;als het mobiel geen mobiel is wordt er veronderstelt dat men
;het gewicht vast heeft...
mobiel))
;een mobiel is gebalenceerd als
; het linkergewicht . l1 = rechtergewicht . l2
; EN het linkerhangsel gebalanceerd is
; EN het rechterhangsel gebalanceerd is
;als balanced wordt opgeroepen op een gewicht wordt #t weergegeven
(if (mobiel? mobiel)
(AND (= (* (mobile-weight (linkerhangsel mobiel)) (linkerlengte mobiel))
(* (mobile-weight (rechterhangsel mobiel)) (rechterlengte mobiel)))
(balanced? (linkerhangsel mobiel))
(balanced? (rechterhangsel mobiel)))
#t))
De software firma waar je werkt heeft net een grote opdracht binnengehaald : een echt CAD/CAM systeem. Als een van hun betere software ontwikkellaars moet jij de basisbibliotheek uitbouwen in Scheme.
Question:1. Je begint met het ontwerpen van een generisch frame-work voor enkele geometrische figuren in het carthesische vlak : point (een punt), segment (een lijnstuk) en circle (een cirkel). Met je collega's spreek je volgende constructoren af.
(Make-segment p1 p2) Make a segment with the given start- and end-point
(Make-circle c r) Make a circle with given center and radius.
Answer:
| point | segment | circle | |
| x-coor | x | 'error | 'error |
| y-coor | y | 'error | 'error |
| punt1 | 'error | p1 | 'error |
| punt2 | 'error | p2 | 'error |
| straal | 'error | 'error | r |
| center | (x,y) | |
c |
| surface | 0 | 0 |
De interface :
(make-point x y)
Question:2. Na overleg met je collega's krijg je het groen licht om aan de implementatie te beginnen.
Answer:
(define (make-point x y)
(attach-type 'point (cons x y)))
(define (make-segment p1 p2)
(attach-type 'segment (cons p1 p2)))
(define (make-circle c r)
(attach-type 'circle (cons c r)))
;dan nu de tabel in geheugen steken
(put 'point 'x-coor (lambda (x) (car x)))
(put 'point 'y-coor (lambda (x) (cdr x)))
(put 'point 'punt1 'error)
(put 'point 'punt2 'error)
(put 'point 'straal 'error)
(put 'point 'center (lambda (x) x))
(put 'point 'surface (lambda (x) 0))
(put 'segment 'x-coor 'error)
(put 'segment 'y-coor 'error)
(put 'segment 'punt1 (lambda (x) (car x)))
(put 'segment 'punt2 (lambda (x) (cdr x)))
(put 'segment 'straal 'error)
(put 'segment 'center (lambda (x)
(make-point (/ (+ (x-coor (car x)) (x-coor (cdr x))) 2)
(/ (+ (y-coor (car x)) (y-coor (cdr x))) 2))))
(put 'segment 'surface (lambda (x) 0))
(put 'circle 'x-coor 'error)
(put 'circle 'y-coor 'error)
(put 'circle 'punt1 'error)
(put 'circle 'punt2 'error)
(put 'circle 'straal (lambda (x) (cdr x)))
(put 'circle 'center (lambda (x) (car x)))
(put 'circle 'surface (lambda (x) (* PI (cdr x) (cdr x))))
(operate 'x-coor geomfig))
(define (y-coor geomfig)
(operate 'y-coor geomfig))
(define (punt1 geomfig)
(operate 'punt1 geomfig))
(define (punt2 geomfig)
(operate 'punt2 geomfig))
(define (straal geomfig)
(operate 'straal geomfig))
(define (center geomfig)
(operate 'center geomfig))
(define (surface geomfig)
(operate 'surface geomfig))
(make-hv-rect left-top right-bottom)
Met je collega's definieer de bovenstaande constructor. Daarna
Answer:
| point | segment | circle | rectangle | |
| x-coor | x | 'error | 'error | 'error |
| y-coor | y | 'error | 'error | 'error |
| punt1 | 'error | p1 | 'error | 'error |
| punt2 | 'error | p2 | 'error | 'error |
| straal | 'error | 'error | r | 'error |
| left-top | 'error | 'error | 'error | lt |
| right-bottom | 'error | 'error | 'error | rb |
| center | |
c | |
|
| surface | 0 | 0 |
|
;de constructor
(define (make-rectangle lt rb)
(attach-type 'rectangle (cons lt rb)))
(put 'point 'left-top 'error)
(put 'point 'right-bottom 'error)
(put 'segment 'left-top 'error)
(put 'segment 'right-bottom 'error)
(put 'circle 'left-top 'error)
(put 'circle 'right-bottom 'error)
(put 'rectangle 'x-coor 'error)
(put 'rectangle 'y-coor 'error)
(put 'rectangle 'punt1 'error)
(put 'rectangle 'punt2 'error)
(put 'rectangle 'straal 'error))
(put 'rectangle 'left-top (lambda (x) (car x)))
(put 'rectangle 'right-bottom (lambda (x) (cdr x)))
(put 'rectangle 'center (lambda (x)
(make-point (/ (+ (x-coor (car x)) (x-coor (cdr x))) 2)
(/ (+ (y-coor (car x)) (y-coor (cdr x))) 2))))
(put 'rectangle 'surface (lambda (x)
(* (- (y-coor (cdr x)) (y-coor (car x)))
(- (x-coor (cdr x)) (x-coor (car x))))))
(define (left-top geomfig)
(operate 'left-top geomfig))
(define (right-bottom geomfig)
(operate 'right-bottom geomfig))
(enclosing-HV-rect figure)
;answer the smallest enclosing HV-rect for a figure
Als je de nodige aanpassingen doorvoert blijken de voordelen van je aanpak nu pas echt naar boven te komen. Nietwaar ?
Answer:
Je kan nu een extra operator toevoegen in de tabel die als functieresultaat de HV-rect bevat. Een beter oplossing is het vervolledigen van de top-left en right-bottom procedures.
| point | segment | circle | rectangle | |
| x-coor | x | 'error | 'error | 'error |
| y-coor | y | 'error | 'error | 'error |
| punt1 | 'error | p1 | 'error | 'error |
| punt2 | 'error | p2 | 'error | 'error |
| straal | 'error | 'error | r | 'error |
| left-top | |
c-r | lt | |
| right-bottom | |
c+r | rb | |
| center | |
c | |
|
| surface | 0 | 0 |
|
(put 'point 'left-top (lambda (x) x))
(put 'point 'right-bottom (lambda (x) x))
(put 'segment 'left-top (lambda (x)
(make-point (min (x-coor (car x)) (x-coor (cdr x)))
(min (y-coor (car x)) (y-coor (cdr x))))
(put 'segment 'right-bottom (lambda (x)
(make-point (max (x-coor (car x)) (x-coor (cdr x)))
(max (y-coor (car x)) (y-coor (cdr x))))
(put 'circle 'left-top (lambda (x)
(make-point (- (x-coor x) r)
(- (y-coor x) r))))
(put 'circle 'right-bottom (lambda (x)
(make-point (+ (x-coor x) r)
(+ (y-coor x) r))))
(define (enclosing-HV-rect figure)
(make-rect (operate 'left-top figure)
(operate 'right-bottom figure)))
(intersects? figure1 figure2)
;answer whether figure1 intersects with figure2
Documenteer (a.h.v. een tabel) en implementeer bovenstaande operatie. Denk na over de gevolgen.
Answer:
| intersects | point | segment |
| point | de punten zijn gelijk | ligt het punt op het segment |
| segment | ligt het punt op het segment | snijden de twee segmenten |
| circle | ligt het punt op de cirkel | snijdt het segment de cirkel |
| rectangle | ligt het punt op de rectangle | snijdt het segment één van de zijden van de rectangle |
| intersects | circle | rectangle |
| point | ligt het punt op de cirkel | ligt het punt op de rectangle |
| segment | snijdt het segment de cirkel | snijdt het segment een van de zijden |
| circle | snijden de twee cirkels | snijdt de cirkel 1 van de zijden |
| rectangle | snijdt de cirkel 1 van de zijden | snijdt 1 van de zijden een zijde van de andere rectangle |
Je ziet dat deze tabel gigantisch wordt als je meer typisch gaat gebruiken. Deze tabel kan verkleint worden door allerlei trucjes te gebruiken.
a. Je ziet dat al de vakjes met coordinaat x,y dezelfde tekst bevatten als de vakjes met coordinaat y,x. Dit zorgt er voor dat de helft van de tabel weggelaten kan worden.
| intersects | point | segment |
| point | de punten zijn gelijk | ligt het punt op het segment |
| segment | turn | snijden de twee segmenten |
| circle | turn | turn |
| rectangle | turn | turn |
| intersects | circle | rectangle |
| point | ligt het punt op de cirkel | ligt het punt op de rectangle |
| segment | snijdt het segment de cirkel | snijdt het segment een van de zijden |
| circle | snijden de twee cirkels | snijdt de cirkel 1 van de zijden |
| rectangle | turn | snijdt 1 van de zijden een zijde van de andere rectangle |
b. Als je nu elk point opwaardeert naar een segment met hetzelfde beginpunt en eind-punt dan valt weer een ganse rij & kolom weg.
| intersects | segment | circle | rectangle |
| segment | snijden de twee segmenten | snijdt het segment de cirkel | snijdt het segment een van de zijden |
| circle | turn | snijden de twee cirkels | snijdt de cirkel één van de zijden |
| rectangle | turn | turn | snijdt 1 van de zijden een zijde van de andere rectangle |
c. een rectangle is een verzameling van 4 segmenten. Als je bij elke rectangle nu telkens vier segmenten gaat snijden dan verliest men weer een rij & een kolom. Men moet wel de procedure schrijven die kijkt of dat men met een rectangle te doen heeft.
| intersects | segment | circle |
| segment | snijden de twee segmenten | snijdt het segment de cirkel |
| circle | turn | snijden de twee cirkels |
(lambda (s1 s2)
;hier komt de routine die controleert of twee segmenten
;snijden
))
(put 'segment 'circle 'turn)
(put 'circle 'segment
(lambda (c s)
;hier komt de routine die kijkt of s c snijdt
))
(put 'circle 'circle
(lambda (c1 c2)
;hier komt de routine die kijkt of ze snijden
))
(define (intersects? figure1 figure2)
(define (intersectrect r f)
(let* ((lt (left-top r))
(rb (right-borrom r))
(lb (make-point (x-coor lt) (y-coor rb)))
(rt (make-point (x-coor rb) (u-coor lt))))
(or (intersects? (make-segment lt rt) f)
(intersects? (make-segment rt rb) f)
(intersects? (make-segment rb lb) f)
(intersects? (make-segment lb lt) f))))
(cond ((eq? (type figure1) 'point)
(intersects? figure2 (make-segment figure1 figure1)))
((eq? (type figure2) 'point)
(intersects? figure1 (make-segment figure2 figure2)))
((eq? (type figure1) 'rectangle)
(intersectrect figure1 figure2))
((eq? (type figure2) 'rectangle)
(intersectrect figure2 figure1))
(else
(let ((proc (get (type figure1) (type figure2))))
(if (eq? proc 'turn)
(intersects? figure2 figure1)
(proc figure1 figure2))))))
Question:1. Definieer een procedure (FLIP) die 1 teruggeeft bij de eerste oproep, 0 bij de tweede oproep, 1 bij de derde oproep, enz...
>>>(flip)
1
>>>(flip)
0
>>>(flip)
1
>>>(flip)
0
Gebruik het environment model om elke oproep van flip te analyseren.
Answer:
(let ((state #f))
(lambda ()
(set! state (not state))
(if state 1 0))))
Answer:
(let ((state #f))
(lambda ()
(set! state (not state))
(if state 1 0))))
(define flip (make-flip))
(define flap1 (flip))
(define (flap2) (flip))
(define flap3 flip)
(define (flap4) flip)
Wat is dan de waarde van de volgende expressies (indien ze in volgorde geëvalueerd worden)
Answer:
flap1 : in het omgevingsdiagram zie je duidelijk dat flap1 gedefinieerd is als 1. Dus het resultaat zal 1 zijn.
flap2 : is gedefinieerd als een procedure. Het resultaat is dus : #<PROCEDURE>
flap3 : flap3 is een andere naam voor flip, wat een procedure is. Dus : #<PROCEDURE>
flap4 is eveneens een procedure (zie diagram) : #<PROCEDURE>
(flap1) : Flap1 is 1. De evaluatie van (1) zal dus als antwoordt hebben : 1 is geen procedure
(flap2) zal een lege doos aanmaken (met geen parameters dus) onde de global environment en dan (flip) evalueren. Dit wil zeggen dat state op #f komt en dat 0 wordt weergegeven.
flap1 is nog steeds 1
(flap3) is nog steeds een andere naam voor flip. Flip wordt dus geëvalueerd. state op #f en resultaat 0
Question:4. Definieer een functie f zodat (+ (f 0) (f 1)) 1 teruggeeft als in jouw Scheme versie de operander van rechts naar links worden geëvalueerd, 0 indien ze van links naar rechts worden geëvalueerd.
Answer:
(let ((flip (make-flip)))
(lambda (x)
(if (= (+ x (flip)) 0)
1
0))))
(define acc (make-account 100 'secret password)) ==> acc
((acc 'secret-password 'withdraw) 40) ==> 60
((acc 'some-other-password 'deposit) 50) ==> Incorrect Password
Answer:
(define (withdraw amount)
(if (>= balance amount)
(set! balance (- balance amount))
"insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount)))
(define (status) balance)
(define (foreign-deposit amount value)
(set! balance (+ balance (* amount value))))
(define incorrect
(lambda x "incorrect password"))
(define (dispatch pass m)
(cond ((not (eq? pass passwd)) incorrect)
((eq? m 'withdraw) withdraw)
((eq? m 'deposit) deposit)
((eq? m 'status) status)
((eq? m 'foreign-deposit) foreign-deposit)
(else (error "Unkown request -MAKE-ACCOUNT" m))))
dispatch)
Answer:
(lambda () (set! seed (quotient (* vorige a) m))))
(define rand (make-random (-1+ (expt 2 32)) (expt 7 5) 4369)
dan produceert (rand 'generate) een nieuw random getal en ((rand 'reset) <new-seed>) reset de interne variabele op de waarde <new-seed>.
Answer:
(lambda (x)
(cond ((eq? x 'generate) (set! seed (modulo (* seed a) m)))
((eq? x 'reset) (lambda (aaargh) (set! seed aaargh)))
(else (error "RANDOM GENERATOR")))))
(define (make-withdraw initial-amount)
(let ((balance initial-amount))
(lambda (amount)
(if (>= balance amount)
(begin (set! balance (- balance amount)) balance)
"Insufficient funds"))))
Answer:
Question:1. Gegeven de definities
(define x (list '(a b) '(c d)))
(define y (list (cons x (cdr x)))
Geef het resultaat van de evaluatie (in volgorde) van volgende expressies (teken box-pointer diagrammen) :
y
(car (car y))
(car (cdr y))
(set-car! (car y) (cdr y))
y
x
Answer:
(car (car y)) geeft (A B)
(car (cdr y)) geeft (C D)
Om het duidelijk te houden teken ik eerst hoe de structuur eruit ziet in geheugen.
Dan pleeg ik nu een (set-car! (car y) (cdr y))
Question:2. Je wil een functie schrijven die het aantal cons-cellen in een struktuur telt. Toon aan dat onderstaande procedure count-pairs niet het gewenste resultaat geeft door box-pointer digrammen met 3 cellen te tekenen, waarvoor het resultaat van count-pairs respectievelijk resulteert in 3, 4, 7 en een oneindelige lus. Schrijf expressies om die structuren aan te maken.
Answer:
(if (not (pair? x))
0
(+ (count-pairs (car x))
(count-pairs (cdr x))
1)))
(define 3-ring '(1 2 3))
(define 4-ring
(let ((last-cel (cons 'lastcar 'lastcdr)))
(cons last-cel (cons last-cel '()))))
(define 7-ring
(let* ((third (list 3))
(second (cons third third)))
(cons second second)))
(define infinite-ring
(let* ((third (list 3))
(first (list 1 third)))
(set-cdr! third first)))
Answer:
(define (make-list n result)
(if (= n 0)
(cons 0 result)
(make-list (-1+ n) (cons n result))))
(let* ((last-cel (list (-1+ n)))
(first-cel (make-list (- n 2) last-cel)))
(set-cdr! last-cel first-cel)
first-cel))
(define (show-ring r)
(display (car r))
(display " ")
(show-ring (cdr r)))
Answer:
(cdr r))
Answer:
(define (loop-until-cdr-eq? lst cdrmustbe)
(if (eq? (cdr lst) cdrmustbe)
lst
(loop-until-cdr-eq? (cdr lst) cdrmustbe)))
(loop-until-cdr-eq? r r))
(define (show-ring-rev r)
(display (car r))
(display " ")
(show-ring-rev (rotate-right r)))
Answer:
(define checklist '())
(define (loop r)
(cond ((null? r) #f)
((memq r checklist) #t)
(else
(set! checklist (cons r checklist))
(loop (cdr r)))))
(loop r))
(define (cycles-2? r)
(define (check-until-pos lst pos wat)
(if (= pos 0)
#f
(if (eq? lst wat)
#t
(check-until-pos (cdr lst) (-1+ pos) wat))))
(define (looplst lst aantal)
(cond ((null? lst) #f)
((check-until-pos r aantal lst) #t)
(else (looplst (cdr lst) (1+ aantal)))))
(looplst r 0))
Answer:
(define (append-ring r stop resultfirst resultlast)
(if (eq? r stop)
(begin
(set-cdr! resultlast resultfirst)
resultfirst)
(begin
(set-cdr! resultlast (list (car r)))
(append-ring (cdr r) stop resultfirst (cdr resultlast)))))
(let ((first-cell (cons (car r) '())))
(append-ring (cdr r) r first-cell first-cell)))
Answer:
(define (remove-n r aantal)
(if (= aantal 1)
(begin
(set-cdr! r (cddr r))
(cdr r))
(remove-n (cdr r) (-1+ aantal))))
(define (while-not-1 r)
(if (eq? (cdr r) r)
(car r)
(while-not-1 (remove-n r n))))
(while-not-1 (copy-ring r)))
Question:1. Implementeer het ADT queue (zie cursus blz 87) met message passing stijl. Breid uit met een "display" procedure om de queue af te printen.
Gebruik deze om een stuk scheme code te schrijven dat
Answer:
(define rear #f)
(define first #f)
(define (enqueue el)
(if (not first)
(begin
(set! rear (list el))
(set! first rear))
(begin
(set-cdr! rear (list el))
(set! rear (cdr rear))))
#t)
(define (dequeue)
(if (not first)
#f
(let ((result (car first)))
(set! first (cdr first))
result)))
(define (show)
(display first)
(newline))
(define (queue mesg)
(cond ((eq? mesg 'enqueue) enqueue)
((eq? mesg 'dequeue) dequeue)
((eq? mesg 'display) show)
(else (error "Queue-, unkown message"))))
queue)
(define (demo)
(define Q (make-queue))
(define (first-five)
(do ((nogtedoen 5 (-1+ nogtedoen)))
((= nogtedoen 0) #t)
(display ((Q 'dequeue)))))
(do ((pos 1 (1+ pos)))
((= pos 11) #t)
((Q 'enqueue) pos))
((Q 'display))
(first-five)
((Q 'display))
(first-five))
de syntax van do :
(do ((<naam> <init> <step>)
(... ... ... )
(... ... ... ))
((<stop-cond>) <resultaat>)
<body>)
(define (stack-push stack el) ...) ;bijvoegen van een element
(define (stack-pop stack) ...) ;afhalen van het top-element
(define (stack-empty? stack ...) ;testen of de stack leeg is
Answer:
(define (create-stack)
(let ((stack (make-stack)))
(define (push e)
(set! stack (stack-push e stack)))
(define (pop)
(set! stack (stack-pop stack)))
(define (empty?)
(stack-empty? stack))
(define (dispatch mesg)
(cond ((eq? mesg 'pop) pop)
((eq? mesg 'push) push)
((eq? mesg 'empty?) empty?)
(else (error "aargl"))))
dispatch))
;en dan nu als de interface destructief is
(define (create-stack)
(let ((stack (make-stack)))
(define (push e)
(stack-push e stack))
(define (pop)
(stack-pop stack))
(define (empty?)
(stack-empty? stack))
(define (dispatch mesg)
(cond ((eq? mesg 'pop) pop)
((eq? mesg 'push) push)
((eq? mesg 'empty?) empty?)
(else (error "aargl"))))
dispatch))
(let ((table (make-table)))
(define (lookup-or-compute x)
(let ((previously-computed-result (lookup x table)))
(if (not (null? previously-computed-result))
previously-computed-result
(let ((result (f x)))
(insert! x result table)
result))))
lookup-or-compute))
(define memo-fib
(memoize
(lambda (n)
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (memo-fib (- n 1))
(memo-fib (- n 2))))))))
(define (fib n)
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (fib (- n 1))
(fib (- n 2))))))
Answer:
(define (lookup wat table)
(let ((answer (assoc wat (car table))))
(if answer
(cdr answer)
#f)))
(define (insert! wat1 wat2 table)
(set-car! table (cons (cons wat1 wat2) (car table))))
(define (memoize f)
(let ((table (make-table)))
(define (lookup-or-compute x)
(let ((previously-computed-result (lookup x table)))
(if (not (null? previously-computed-result))
(begin
(display "Memo-fib ")
(display x)
(display " uit tabel")
(newline)
previously-computed-result)
(begin
(display "Memo-fib ")
(display x)
(display " berekent")
(newline)
(let ((result (f x)))
(insert! x result table)
result)))))
lookup-or-compute))
Memo-fib 3 berekent
Memo-fib 2 berekent
Memo-fib 1 berekent
Memo-fib 0 berekent
Memo-fib 1 uit tabel
Dit werkt niet meer als we gewoon (memoize fib) hadden gebruikt omdat de recursieve aanroep fib aanroept inplaats van (memoize fib)
Question:4. Wat is de performantie van Calc-E als we een gememoizeerde versie van factorial gebruiken in onderstaande functie ? Id dat beter dan het antwoord op vraag 3, reeks 3 ?
Answer:
De performantie van
de niet gemoizeerde versie is O(n
![]() ).
Als de factorial gememoizeerd is dan zal deze O(n) zijn.
).
Als de factorial gememoizeerd is dan zal deze O(n) zijn.
Question:1. Maak gebruik van streams om de volgende reeksontwikkeling te berekenen :
Laat ik eerst beginnen met zelf een paar routines te schrijven
(define (enumerate from step)
(cons-stream from (enumerate (+ from step) step)))
(define (accumulate s accumulator init)
;geeft een stream weer te vergelijken met s/(1-x)
(cond ((eq? the-empty-stream (head s))
the-empty-stream)
(else
(let ((el (accumulator (head s) init)))
(cons-stream
el
(accumulate (tail s) accumulator el))))))
(define (map action s)
(if (eq? the-empty-stream s)
the-empty-stream
(cons-stream (action (head s)) (map action (tail s)))))
(define (first n stream)
(if (= n 0)
(begin
(newline)
*the-non-printing-object*)
(begin
(display (head stream))
(display " ")
(first (-1+ n) (tail stream)))))
(define e-stream
(accumulate
(map
(lambda (x) (/ 1 x))
(accumulate
(enumerate 1 1)
*
1))
+ 1))
(define (map proc stream)
(if (empty-stream? stream)
the-empty-stream
(cons-stream (proc (head stream))
(map proc (tail stream)))))
(define (filter pred stream)
(cond ((empty-stream? stream) the-empty-stream)
((pred (head stream))
(cons-stream (head stream)
(filter pred (tail stream))))
(else (filter pred (tail stream)))))
(define (accumulate combiner init stream)
(if (empty-stream? stream)
init
(combiner (head stream)
(accumulate combiner init (tail stream)))))
(define (enumerate-int low high)
(if (> low high)
the-empty-stream
(cons-stream low (enumerate-int (1+ low) high))))
(define (fac x) (if (= x 0) 1 (* x (fac (-1+ x)))))
(define (calc-sin x n)
(accumulate + 0
(map
(lambda (e)
((if (odd? (quotient e 2)) - +)
(/ (expt x e)(fac e))))
(filter
(lambda (n) (odd? n))
(enumerate-int 1 n)))))
Stel dat S is ((1 2 3) (4 5 6) (7 8 9) (10 11 12)) dan (accumulate-n + 0 S) zal de stream (22 26 30) teruggeven.
(cond ((eq? (head s1) the-empty-stream) s2)
((eq? (head s2) the-empty-stream) s1)
(else
(cons-stream
(combiner (head s1) (head s2))
(combine (tail s1) (tail s2) combiner)))))
(define (accumulate-n operator S)
(cond ((empty-stream? s) the-empty-stream)
((empty-stream? (tail s)) (head s))
(else
(accumulate-n operator
(cons-stream
(combine (head s) (head (tail s)) operator)
(tail (tail s)))))))
(define triplet-stream
(map
(enumerate-to 0 3 1)
(lambda (x) (enumerate-to (1+ (* 3 x)) (+ 3 (* 3 x)) 1))))
(define accu-stream (accumulate-n + triplet-stream))
(transpose m)
(filter
(lambda (x) (> (caddr x) max))
(map
(lambda (couple) (list (car couple) (cadr couple)
(+ (car couple) (cadr couple))))
(flatten
(map
(lambda (i)
(map
(lambda (j) (list i j))
(filter
odd?
(enumerate-int 1 max))))
(filter odd? (enumerat 1 max)))))))
0 de head van de stream wordt reeds geëvalueert
X het resultaat van de define
» (head (tail x))
1 Ik vraag de tail, dus berekent hij deze
1 het resultaat van head en de volledige expressie is dan 1
» (head (tail x))
1 De tail moet niet meer berekent worden, hij is al eens uitgeteld.
» (define x (map show (enumerate-int 0 10)))
0 de head van de stream wordt reeds geëvalueert
X het resultaat van de define
» (head (tail (tail (tail x))))
1 (tail x) wordt berekent
2 (tail (tail x)) wordt berekent
3 (tail (tail (tail x))) wordt berekent
3 Het resultaat van de head is dan 3
