Home Papers Reports Projects Code Fragments Dissertations Presentations Posters Proposals Lectures given Course notes

The hidden cost of Suballocators

Werner Van Belle1 - werner@yellowcouch.org, werner.van.belle@gmail.com

1- Yellowcouch;

Abstract :  In this report we describe a number of overhead estimates a suballocator might incur on 'smaller' memories. The report is mainly aimed at illustrating the strengths and weaknesses when one considers the option of allocation large chunks of similarly sized data to save space.

Keywords:  memory management, suballocator
Reference:  Werner Van Belle; The hidden cost of Suballocators; Computer Science; YellowCouch; December 2010


Table Of Contents
Introduction
Memory Layout
    The block meta information
    The element freelist in a block
Target block size
    Overhead for large blocks
    Target block size for small elements
    Intermediate block sizes
    Overhead for elements of 1 byte
Incompletely filled blocks
    Overhead in 1 incompletely filled block
    Overhead in t blocks of same elementsize
Tradeoff between blocksize, efficiency and required data to store
Conclusion

Introduction

Most memory allocators allocate each individual element as its own 'chunk', containing the size prefixed, potentially some extra meta information and the actual content. When we allocate many small chunks, e.g: 3000 allocations of 40 bytes each, then this size (assumed to be 4 bytes representing the length) will directly lead to an overhead of 10%.

Suballocators solve this problem by allocating for each different size of allocations a larger block of memory. Instead of allocating 3000 individual chunks, a suballocator will allocate 1 block of 3000 chunks, leading to a much smaller overhead.

Of course there are a number of problems with this approach. First and foremost, allocating larger blocks incurs an overhead of empty space that is, in a statistical sense, not used. And secondly, the extra management information required to find blocks of appropriate size incurs another overhead that must be carefully calculated.

Memory Layout

The statistics presented below are based on an actual C++ implementation that is available as a package from [1].

Overall memory layout

The overall memory layout contains 6 starting records. Some of these records point to the root of a number of search trees we deal with. Others form sentinels, to point to the first and last block. After the initial records come a collection of blocks. Each block contains a starting record, which we will describe below, and then a number of 'chunks' (or elements), all of the same size.

The block meta information
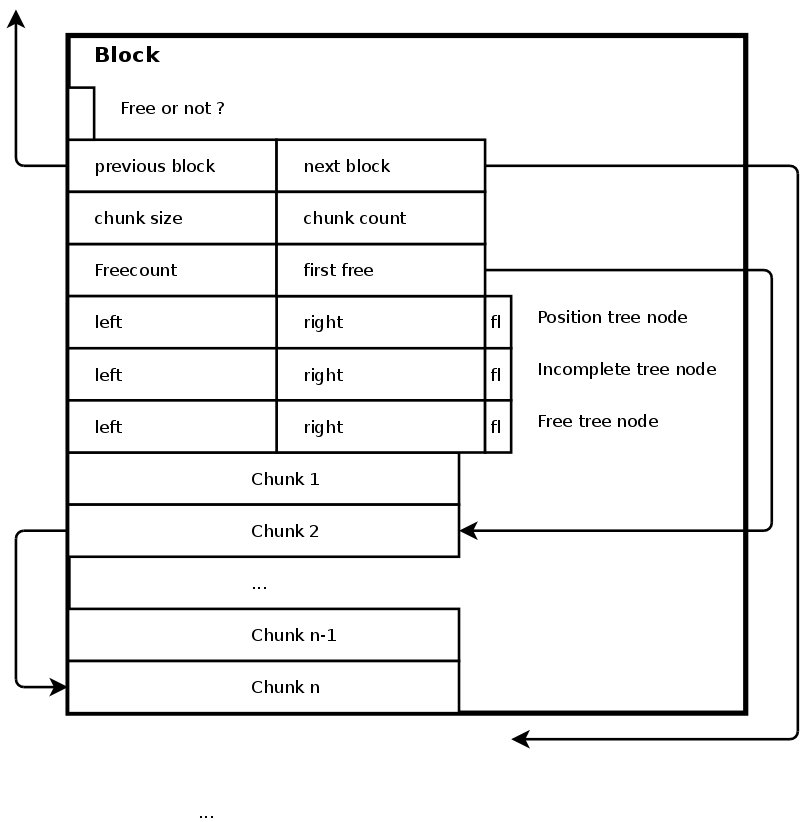The starting record of a block

All memory blocks contain the following information

In total, each blocks header is thus 100 bytes long. If we however would compress and make certain things overlap better we would of course end up with a better estimate. In particular:

In summary, we can work with 40 bytes (if we deal with a 32 bit memory), or with a 80 byte block header (in case of a 64 bit addressing scheme).

The element freelist in a block

The freelist of elements/chunks in a block works as follows:

In case the chunksize is larger than 4 (or 8) bytes, then the freelist can directly point to the actual addresses.

A problem appears when the 'next' pointer cannot be stored within the required chunk size. Such situations arise when we allocate blocks that deal with chunks of size 1,2 or 3 (and maybe 4,5,6 or 7). When this happens, it is suffices for most cases to refer to element indices instead of addresses. Even when allocating elements of 2 bytes long, will it suffice for most purposes.

However, if we want to go the insane way of allocating many single bytes, then we can be creative and use the freepointer its 4 (or 8) bytes to refer to specific element starts. The first byte of the freepointer would then deal with the first subchunk of the block (the first 256 bytes). The second byte of the freepointer would then deal with the second subchunk of the block (byte 256-511) and so on. Using this approach we can only deal with 1024 (or 2048) bytes. It is however a very weird thing to require for the allocation of a simple bytes. Especially because the pointer to such a byte itself would already be longer than the byte. Nevertheless, when programming it can sometimes occur that the programmer does not want to deal with cases where the string is suspiciously short. So therefore we must allow this to occur and we should be able to deal with it.

Target block size

Because the size of a block is a somewhat arbitrary choice. E.g: do we really need to allocate 100'000 single bytes, if a request for a single byte comes in, or might it be more economic to allocate only 1024 elements at a time ? In case we deal with large blocks we obviously do not even want to do that, that would mean allocating 1024 elements of 1Mb !

To deal with this aspect of the statistics it is in general better to try to make all blocks of similar length: E.g 8192 bytes, or 16384 bytes, unless the required element size becomes larger than the blocksize itself. In which case, the block will contain only 1 element.

Estimating the overhead, with which we mean, the number of empty bytes or bytes allocated to meta information, in ratio to the number of useful bytes, is not straightforward. We will ask the following questions

  1. What is the overhead within one block if it has been completely filled ?
  2. What is the overhead when we deal with incompletely filled blocks

Both cases will be approached under the assumption that we deal with an blockheader of 36 (in case of 32 bits per pointer), or 72 bytes (in case of 64 bits per pointer), as a theoretical attainable target. We will also be considering different target block sizes.

We will rely on a number of variables

Overhead for large blocks

When an element is allocated that is larger than the required chunk size then only 1 element will be stored, in the block, meaning that the overhead is given by the elements size (s) and the overhead (c), as c/(s+c)

If we want to reach an efficiency of E for single element blocks, then the minimum block size must be


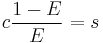
An efficiency of 1% is reached if we store an element of 3564 bytes directly in its own block (32 bit), or 7128 (64 bit).

Target block size for small elements

The overhead per block, of length n, is given as the total allocated memory (n) divided by the useful memory (n-c), subtract 1.


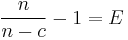
If we want this to reach a specific efficiency. E.g 1%, then we


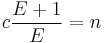
To reach an efficiency of 1%, we will need to have block sizes of 3636 bytes (32 bit pointers), or 7272 bytes (64 bit pointers). This is already somewhat of a surprise that simply the pointer size will force us to allocate twice as many elements per block

Together with this result we find that we can describe the number of elements we must place in this type of blocksize. i=(n-c)/s

  1. s reflects the element size
  2. i reflects the number of elements

For elements of size 2, we will allocate 1800 elements (32 bit), 3600 (64 bit). For elements of size 4, we will allocate 900/1800 elements per block.

Intermediate block sizes

We already figured out that storing an element of 3564 bytes in its own block leads to an efficiency of 1%, and that completely filled blocks with a blocksize must have a size larger than 3636 bytes.

The question now becomes, what happens if we have sizes that cannot be easily doubled into a block: E.g: an element size of 3500. If is clearly less than 3564, so we want multiple elements, but we cannot store two of them in 3636 bytes. In this case, it is useful to take the minimum number of elements to be larger than 3636 bytes.

Overhead for elements of 1 byte

If we deal with very small elements of 1 or 2 bytes, we have a limit on the number of elements we can store. If a block of element size 2 we can at most store 65535 elements. This is already much larger than the required minimum blocksize and is thus not a problem.

If we store single elements, we can store up to 1024 element (32 bit), or 2048 (64 bit), which leads to the unavoidable overhead of 3.396%

Incompletely filled blocks

Overhead in 1 incompletely filled block

When a block of size n is filled half, we have c+(n-c)/2 useless bytes. (the first c is the start meta information, and then half of the block has turned out to be useless). This gives an overhead of



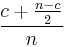
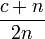
which leads to an overhead of 50.5%. Quite a disaster indeed. This might even be worse. The chance that a single memory allocation of 3023 elements take place is much higher than this element being allocated twice, leading to the question whether we should indeed allocate such not large enough, yet not sufficiently small elements twice.

In case the element size is a seldom occurring element (a string of 213 bytes), we will still allocate 3636 bytes, leaving us with an overhead of 94.1%. This is an even bigger disaster. Tuning this type of information might require the ability to split a block when it has not been used for a long time. Another strategy might require us to rely on the memory allocation size distribution, and set an appropriate cutoff value at which point we will no longer allocate multiblocks, instead we might rely on single blocks.

Overhead in t blocks of same elementsize

If we would need to allocate 2 blocks of the same elementsize, we would of course see this overhead to about 75%, and if we allocate t blocks of a certain element size, then we would be allocating t*n bytes, in which, for the first (t-1) blocks (n-c) bytes are actually useful. For the last block we would have (n-c)/2 useful bytes. Expressed in overhead: for the first t-1 blocks, we would have a total overhead of (t-1)*c, while the last block would have an overhead of (c+n)/2.



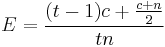
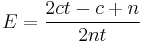
and


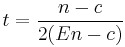
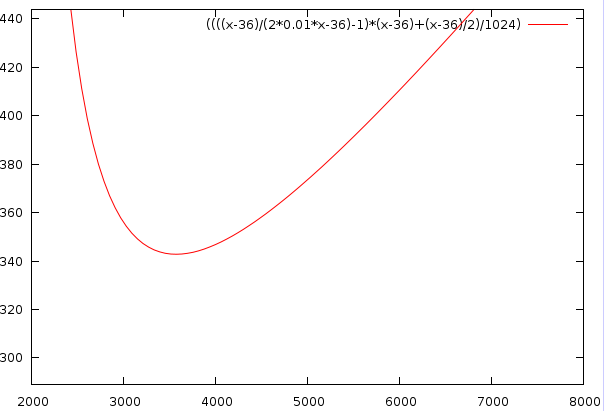
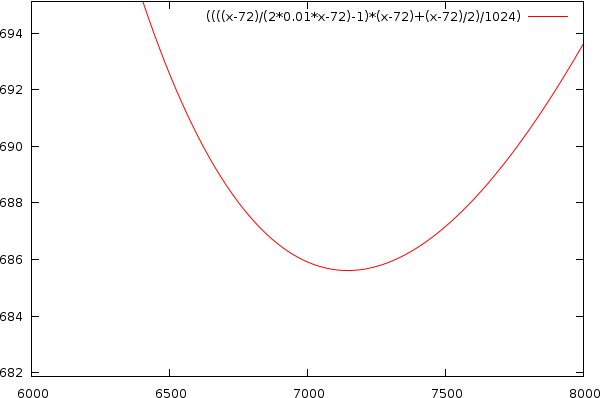
This means that to achieve an efficiency of 1%, with c=36 and a blocksize of n=3636 bytes, we need about 5000 ! blocks. This is mainly due to our choice of minimal blocksize. If we choose larger block sizes, it becomes easier to achieve better performances. E.g, When using a target size of 8192 we only need 88 blocks to reach said efficiency. A plot is shown below

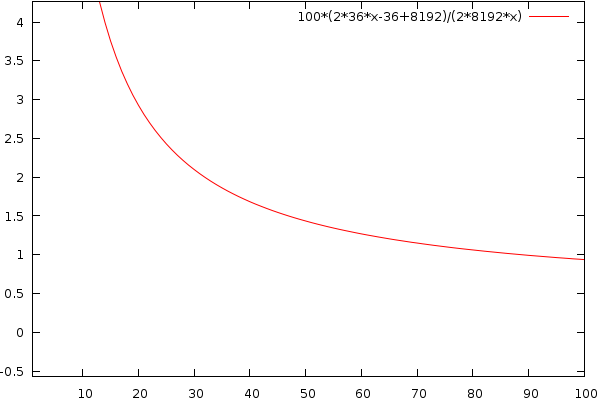Plot showing the overhead when we need to allocate x blocks of 8192 byes

The drama of this cannot be underestimated. Although the estimates we gave when blocks were completely full, the fact that a block will seldom be complete full requires us to allocate much, much, much more than we originally anticipated. As an example: with 88 blocks needed to allocate, we must allocate 704 Kb to deal with, for instance the 4 byte elements, or the 8 byte elements, and then the 16 byte elements. For each of these potential sizes we must at least have 704kb data to store, otherwise are overhead will be larger than 1%.

Tradeoff between blocksize, efficiency and required data to store

To calculate the trade off between blocksize, blockcount to reach 1% efficiency and the required amount of data to store, we combine the various variables. The blocksize is again given by n. The blockcount required to reach the appropriate efficiency has been given before. The amount of data to store is given by the blockcount tmultiplied with the blockload (n-c) for the first t-1 elements, and then (n-c)/2 for the last one. Which gives as stored data amount


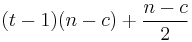
Substituting the required blockcount under blocksize n, gives


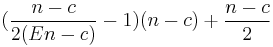
and we can plot a graph with on the horizontal axis the blocksize and on the vertical axes the kilobytes of data necessary to store, before we will reach that efficiency.

c=36 (32 bit pointers) c=72 (64 bit pointers)

Vertical: the required amount of data to store in equally sized elements to reach 1% efficiency, given a certain target blocksize (n), shown horizontally.

Conclusion

The memory allocator we presented seems to achieve great efficiency if we compare the used memory against the allocated memory. That is if we assume fully allocated blocks.

That is however not very likely to happen. There will always be blocks partly filled, which leads to a drastic reduction in performance. There seems to be a trade off between the target blocksize and the amount of data that needs to be stored before the allocator reaches a certain efficiency. To achieve an efficiency of 1%, the ideal blocksize would be around 100 times larger than the blockheader size. And in that case the minimal amount of data to store to reach that efficiency is about 10'000 times more than the blockheader size. In words: to achieve an efficiency of 1% in a 64bit memory we require to store around 720KB of equally sized elements.

This also means that every byte we can remove from the blockheader reduces the required data to store with 9.7 kB.

In conclusion, this allocator is well suited for very very large memory requirements. When dealing with a 64bit memory, an optimal dataset will require 9.7 GB of data. In practice that would, due to the non-uniform distribution of allocationsizes easily jump up 4 orders of magnitude. So when dealing with terabytes (or even petabytes) of information, then this allocator might become efficient. Sadly enough, in such situations, location of data as well as access times (thinking of the balanced tree), might become more of a burden than the speed-efficiency itself.

In truth, this was a nice algorithm to work with, a nice idea, but achieving an efficiency of 1% can easily be obtained using other methods, such as adaptations of the dough-lea allocator, using variable sized pointers (local and remote), letting the program deal with block allocations instead of the memory allocator, or a hybrid approach in which block allocation happens only for a limited number of element sizes (e.g: those below 200 bytes).

So all in all it is quite worthless. ... but you can still download the artefact:

1.The Extreme SubAllocator Werner Van Belle ftp site on ftp://ftp.yellowcouch.org/tools/suballocator-0.1.tgz ftp://ftp.yellowcouch.org/tools/suballocator-0.1.tgz
http://werner.yellowcouch.org/
werner@yellowcouch.org