| Home | Papers | Reports | Projects | Code Fragments | Dissertations | Presentations | Posters | Proposals | Lectures given | Course notes |
|
Detecting Transients in AudioWerner Van Belle1 - werner@yellowcouch.org, werner.van.belle@gmail.com Abstract : Explained is a transientdetector to detect changes in frequency or volume.
Keywords:
transients, transient detector, groupdelay, phase responce |
Table Of Contents
| Introductiveness | Group Delay A tick A change in frequency Algorithm |
Introductiveness
Transients are important for time pitch modifications. When slowing down, one wants to avoid repeating transients, while, when speeding up one does not want to skip transients. Measuring transients allows us to segment music in easily digestable chopped up pieces, making sample reshuffling possible. Measuring transients is a tricky thing. Quoting Julius Orion Smith: it leads to deeply philosophical discussions.
At first glance measuring the places where a large volume change takes place should suffice. Hi hats and strong sounds can be detected that way. The problem is of course that it cannot deal with hi hats under a thick coat of ambient atmosphere.
At second glance, a position in music is also 'transient' when the central frequency changes. Below we present a technique that detects both types of transients in a straightforward manner. Only the main points are summarized.
Group Delay
The technique measures the group delay of windowed pieces of sound, thereby we assume that each window is a filter to be applied to a tick. By measuring the group delay that tick will undergo, we know where the tick will end up in the original sound, which thus provides us with the transient positions.
The group delay of a filter is defined by how many samples the envelope of a specific frequency is delayed. It is calculated as the negative differential of the unwrapped phase response. To obtain the phase response of a finite impulse response filter one can apply a simple fourier transform to its coefficients and calculate the phases within that frame.
When calculating the group delay of an audiofragment it is necessary to window that sound before calculating the fourier transform. Otherwise one finds that the typical group delay is 0 (which would be correct because in a cyclic world the transition from the last sample back to the first tends to be discontinuous). Applying a hann window takes care of this obvious problem.
The second problem is the unwrapping of phases. That is done by ensuring that all phase differences fall between 0 and -2Pi. This is contrary to the standard strategy, which targets them to fall within -Pi:Pi. Nevertheless we need group delays that are strictly positive and positioned relative to the start of our audiofragment. Therefore this choice is appropriate and makes our live much less complicated.
As soon as we have a windowed fourier frame with a series of unwrapped phases, we can calculate each frequencies group delay as the negative differential of the phases. Each differential is then a value between 0 and 2 Pi, which corresponds to a delay in samples between 0 and the windowsize. For each frequency we can thus calculate the position at which that frequency is most 'transient'. This information is recorded by marking that position in a secondary array.
To assess the relevance of each transient position we use the log magnitude of the specific fourier bin (a group delay of X for a frequency that is barely audible might help the fourier analysis to reconstruct the audio, but it does have little meaning with respect to the transients we are calculating). Thereby a cutoff-value at for instance -64 dB suffices to deal with the problem of infinities.
Below we show the result of such a transient detector on a tick and a frequency change.
A tick
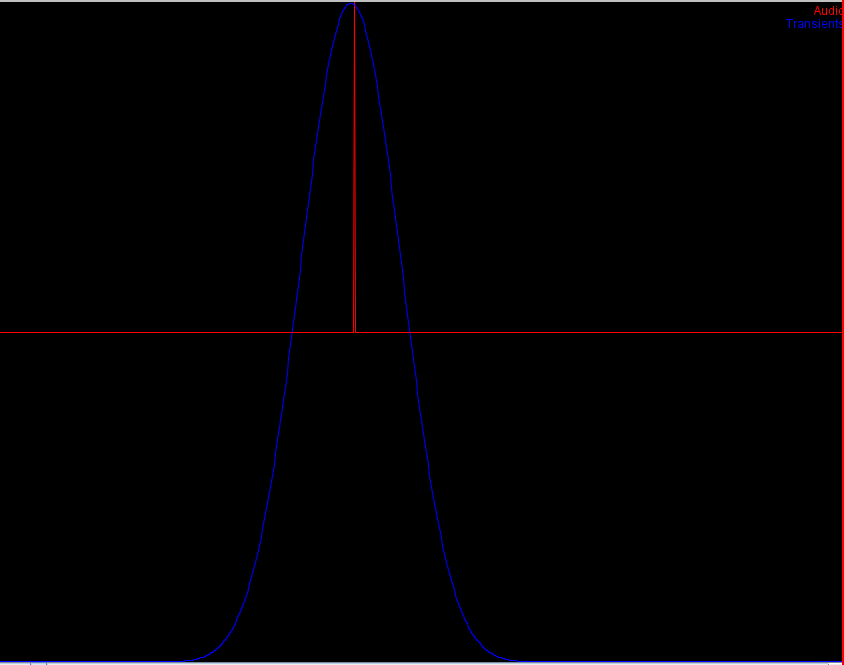The red line is the audio input. The
blue line is the detected transientness of that position
|
A change in frequency
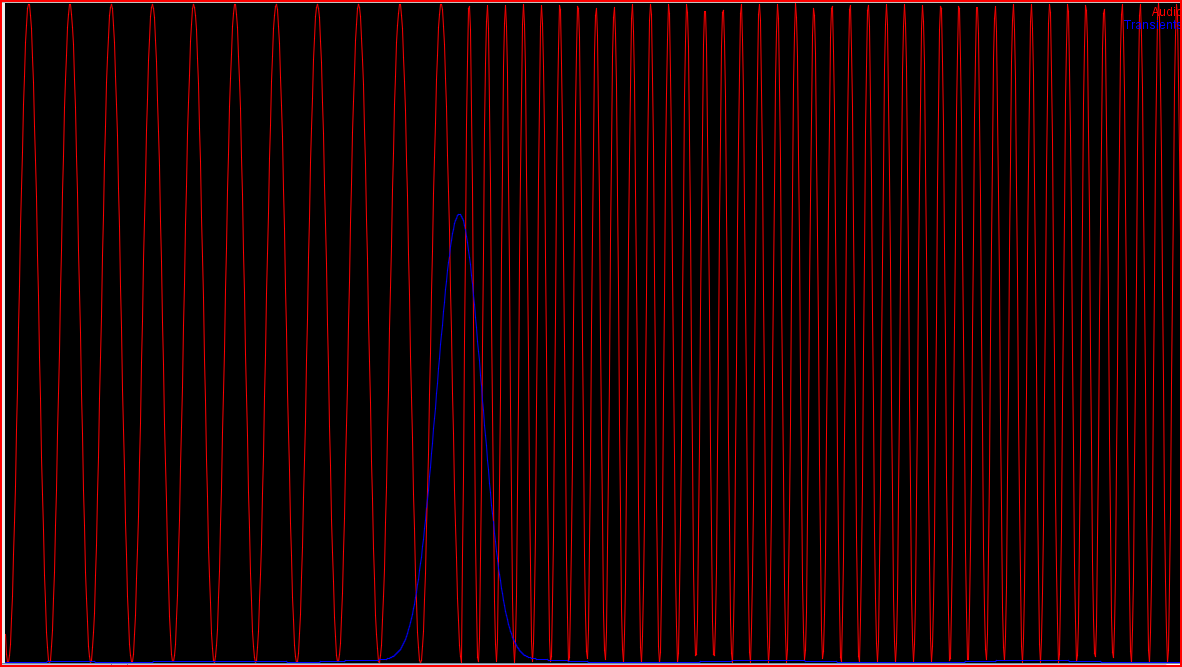The red line is the audio input. The
blue line is the detected transientness of that position
|
Algorithm
An audio block reIn, with size windowsize is used as input. The output is added to a transient array of exactly the same size.
1. apply a hann window to reIn.
2. perform a forward fourier transform of (reIn,0) to (reOut,imOut)
3. prev=0
4. for(i=0;i<windowsize;i++)
{
5. j = imOut[i]
r = reOut[i]
phase = atan2(j,r)
6. phase_difference = phase - prev;
prev = phase
7. unwrap the phase_difference to 0:2PI, such that this is a causal filter starting at window position 0
while( phase_difference < 0 )
phase_difference += 2 * pi;
8. transient_position = phase_difference * windowsize / (2 * pi);
9. weight = log(j * j + r * r);
if (weight>threshold)
transients[transient_position] += weight;
}
This algorithm should be ran over a stream of audio, which is done by merely sliding the window in sufficiently small steps over the audio (E.g: an overlap of 4 to 32 works quite well).
Lastly, the resulting transient array requires some smoothing. A linear phase filter, such as a stacked moving average of order 4 with windowsize 64, suffices to unify the information aggregated from different windows.
Below a demonstration on the transientness of a real piece of audio
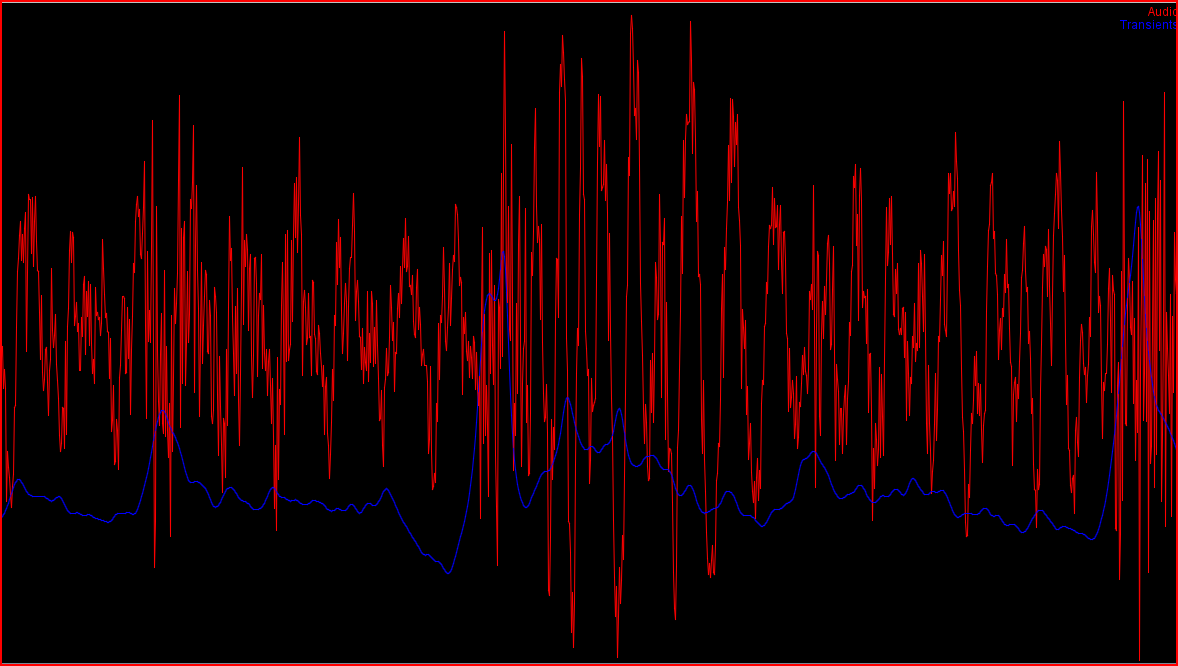The red line is the audio input. The
blue line is the detected transientness of that position
|
| http://werner.yellowcouch.org/ werner@yellowcouch.org |  |