| Home | Papers | Reports | Projects | Code Fragments | Dissertations | Presentations | Posters | Proposals | Lectures given | Course notes |
|
|
Actors for Mobile Ad-Hoc Networks (The Ambient Actor Model)Jessie Dedecker1+ - jededecker@vub.ac.be Abstract : Wireless communication has a limited communication range which introduces two major problems, currently not captured in distributed middleware. First, they are less reliable than their wired variants and secondly they are extremely dynamic. Both problems complicate the development of mobile software. In this paper we extend the operational semantics of the actor model to capture these two properties. We do this by adding a single new concept to the model: the mailbox. This paper provides a foundation for new implementations of the actor language and frameworks that are usable in the context of wireless network environments.
Keywords:
ambient pervasive ubiquitous computing asynchronous distributed systems actor systems |
1 Introduction
Networks formed by the interconnection of mobile wireless devices are often called mobile ad-hoc networks. Developping software to run within mobile ad-hoc networks is extremeley challenging. Firstly because mobile ad-hoc communication is less reliable than fixed topologies. Connections are interrupted as devices move out of communication range. Secondly because mobile ad-hoc communication is more dynamic. Communication partners frequently enter and leave the communication range.
In order to approach these problems we extended the actor model. In the remainder of the paper, we assume familiarity with the actor model, as such we will not fully recapitulate the semantics. These can be found in [AMST97].
2 Actors
2.1 The Actor Programming Language
- create a new actor using letactor primitive. The letactor primitive takes one argument. A function that is the initial behavior of that actor.
- send messages to known actors using the send primitive. The send primitive takes two arguments, the recipient's actor address and a message. Such a message can contain the address of other actors.
- modify its own state and behavior using the become primitive. The become primitive takes one argument, a function that is the new behavior and state of the actor. There is no shared data between actors.
2.2 Actor Systems
2.3 Applicability of Actors in Mobile Ad-Hoc Networks
Actors are a programming model [Agh90] for distributed networks and provide a good groundwork for programming the internet. The actor model makes use of an asynchronous message delivery, that is, it decouples the availability of the communication partners in time. This makes the actor model suitable for open distributed systems and a good candidate for mobile ad-hoc networks. However, the actor model fails to capture certain important concepts:
- the model does not support dynamic communication between different actor systems. Actor systems are connected through a static connection.
- there is no abstract way to find a set of actors that might offer a certain service, or to find actors that are in communication range.
- the model does not support disconnected operations. The actor model assumes that messages sent will eventually be received. In mobile ad-hoc networks this cannot be guaranteed. There is a need for more explicit awareness of availability and control of over message delivery. E.g; when a message is still pending but sending it is no longer necessary, it should be possible to remove it.
- between sending messages and receiving messages the computational context is lost. When a new message arrives the program will need to restore a previous context based on the message. However, because the actor model does not provide suitable primitives, the developer needs to program this functionality, which can be very tedious.
- the availability of actors within mobile ad-hoc networks often change. As such, the application often needs to postpone tasks up to a later moment. At the moment the actor comes in range again, then the postponed task can be resumed, unless of course the task has become obsolete (i.e. because the task could be done at some other place). In mobile ad-hoc networks, actors need to be able to be aware of their environmental context.
3 The Ambient Actor Model
The main addition to the actor model is the introduction of explicit mailboxes. A mailbox is a store of messages. A number of mailboxes are used within the model to guarantee communication. These are the ``in''-box, which keeps track of incoming messages, the ``out''-box, which keeps track of messages that should be delivered to other actor systems, the ``sent''- and the ``rcv''- box which keep track of, respectively, which messages have been sent and which messages have been processed by the actor. Aside from these four standard mailboxes, every actor can create new mailboxes as necessary. Messages can be present in multiple mailboxes at the same time. E.g, a message can be located in the ``sent''-box of the sending actor and the ``in''-box of the receiving actor.
3.1 Messages and Mailbox Associations
3.1.0.1 Messages (
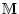 )
)
A message is a pair (pr) of:
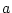 , the actor address of the
receiving actor.
, the actor address of the
receiving actor. 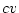 , a communicable value,
constructed from atoms and actor addresses, but not containing lambda
abstractions as specified by Agha [AMST97].
, a communicable value,
constructed from atoms and actor addresses, but not containing lambda
abstractions as specified by Agha [AMST97].
In the extended actor model a message is always associated with at least one mailbox. To denote these mailbox associations in the actor model we introduce the following set:
3.1.0.2 Mailbox Associations (
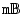 )
)
Denotes a content ![]() associated
with mailbox
associated
with mailbox ![]() .
.
![]() is the set of
identifiers
for mailboxes,
is the set of
identifiers
for mailboxes, ![]() , with
, with
![]() the set of
atoms in the functional language.
the set of
atoms in the functional language. ![]() is the set of actor
addresses.
The mailbox itself is written as an identifier, subscripted with the
name of the actor the mailbox belongs to. E.g.,
is the set of actor
addresses.
The mailbox itself is written as an identifier, subscripted with the
name of the actor the mailbox belongs to. E.g., ![]() denotes the in-box of actor
denotes the in-box of actor ![]() . Typically, messages are associated with a mailbox,
but other values can also be associated with a mailbox.
. Typically, messages are associated with a mailbox,
but other values can also be associated with a mailbox.
3.2 Actor Configurations
The operational semantics of the model itself is based on actor-configurations and reduction rules defined on such a configuration. An actor configuration can be considered to be an actor system as explained in section 2.2. Essentially, an actor configuration can be perceived as all actors present on one computational device, such as an embedded system, a desktop and others. The set of actor configurations is defined as3.2.0.1 Actor Configurations (
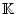 )
)
Say Y is a set then
![]() is the set of
finite subsets of Y.
is the set of
finite subsets of Y. ![]() is the set of
finite multi-sets with elements in Y.
is the set of
finite multi-sets with elements in Y.
![]() is the set of
actor states as defined in [AMST97].
is the set of
actor states as defined in [AMST97].
An actor configuration contains:
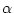 , the state of
the actors in a configuration is given by an actor map
, the state of
the actors in a configuration is given by an actor map 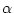 . An actor map is a finite
map from actor addresses to actor states. Each actor state is one of
. An actor map is a finite
map from actor addresses to actor states. Each actor state is one of
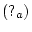 uninitialized
actor state created by an actor named
uninitialized
actor state created by an actor named 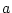
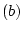 actor state
ready to accept a message where
actor state
ready to accept a message where 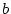 is
its behavior represented by a lambda abstraction
is
its behavior represented by a lambda abstraction ![$ [e]$](img32.png) actor in a
busy state executing expression
actor in a
busy state executing expression 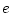 .
. 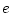 is either a value expression or a
reduction context R filled with a redex
is either a value expression or a
reduction context R filled with a redex 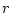 (written as
(written as ![$ {\tt R[}r{\tt ]}$](img35.png) ).
The reduction context is used to identify the subexpression of an
expression that is to be evaluated next. For the formal elaboration we
refer to the original actor model [AMST97].
).
The reduction context is used to identify the subexpression of an
expression that is to be evaluated next. For the formal elaboration we
refer to the original actor model [AMST97].
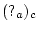 denoted that
uninitialized actor
denoted that
uninitialized actor 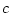 that was
created by actor
that was
created by actor 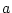 .
. 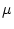 , a multi-set
of mailbox associations.
, a multi-set
of mailbox associations. 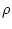 ,
receptionists, the actors from this configuration that are remotely
accessible from other actor configurations
,
receptionists, the actors from this configuration that are remotely
accessible from other actor configurations 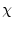 , external
actors, the references to remote actors from other actor configurations
that can be accessed from this actor configuration.
, external
actors, the references to remote actors from other actor configurations
that can be accessed from this actor configuration.
-
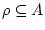 and
and
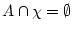 ,
, - if
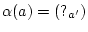 , then
, then 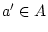 ,
, - if
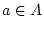 , then FV
, then FV
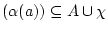 ,
, - if
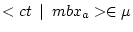 , then
, then 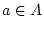
- if
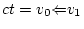 then FV
then FV
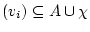 for
for 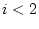
3.3 Operational Semantics of Actor Configurations
On such an actor configuration, a number of reduction rules are defined. Each rule contains a labelThe rules are in
our model are extended with an environmental set ![]() . The set
. The set ![]() contains the actor configurations that are
available (in communication range) while the reduction is performed.
The introduction of this set is important to reify the notion of
environmental context in our extended model. Below we explain and
discuss the different rules.
contains the actor configurations that are
available (in communication range) while the reduction is performed.
The introduction of this set is important to reify the notion of
environmental context in our extended model. Below we explain and
discuss the different rules.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3.3.1 Basic Actor Operations
The first four reduction rules below are the same as defined in [AMST97] and did not need to be adapted:- The
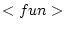 rule above
delegates the purely functional expressions used in the actor program
to the functional redexes. The functional redex contains reduction
rules for function calls, cons-cell manipulation, branch-testing,
type-testing and equality. For the exact definition of these reduction
rules we refer the reader to [AMST97].
rule above
delegates the purely functional expressions used in the actor program
to the functional redexes. The functional redex contains reduction
rules for function calls, cons-cell manipulation, branch-testing,
type-testing and equality. For the exact definition of these reduction
rules we refer the reader to [AMST97].
- The
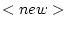 rule is used
to create a new actor with address a'. The
new actor is not initialized after the new
reduction. The new uninitialized actor is denoted with
rule is used
to create a new actor with address a'. The
new actor is not initialized after the new
reduction. The new uninitialized actor is denoted with
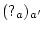 .
. - With the
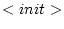 rule a new
actor is initialized with behavior
rule a new
actor is initialized with behavior 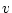 . Only the actor that created the actor a' can initialize it.
. Only the actor that created the actor a' can initialize it. - With the
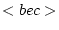 rule the
actor can change its state and its behavior.
The actor address a' is anonymous and thus
unknown to all other actors.
We say that a variable is fresh with
respect to a context of use if it does not occur free or bound in any
syntactic entity.
rule the
actor can change its state and its behavior.
The actor address a' is anonymous and thus
unknown to all other actors.
We say that a variable is fresh with
respect to a context of use if it does not occur free or bound in any
syntactic entity.
3.3.2 Adapted Rules
The remainder of the rules have been adapted to include the notion of mailboxes:- The
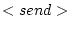 rule differs
from the original send rule. Instead of
placing the message immediately in the message set
rule differs
from the original send rule. Instead of
placing the message immediately in the message set  , we first differentiate on the nature of the
message. If the message can be delivered locally (within the same actor
configuration), it is immediatelly placed in the target its in-box, and
the sent-box of the sender. Otherwise, the message is placed in the
actor its out-box. From there on, through other reduction rules, this
message will be moved to the target its in-box.
, we first differentiate on the nature of the
message. If the message can be delivered locally (within the same actor
configuration), it is immediatelly placed in the target its in-box, and
the sent-box of the sender. Otherwise, the message is placed in the
actor its out-box. From there on, through other reduction rules, this
message will be moved to the target its in-box. 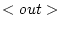 We write FV(e) for the set of free variables of
We write FV(e) for the set of free variables of 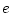 . Messages that cannot be delivered
locally, will be placed in the out-box of the sending actor. The out
reduction rule is used, at the sending side, to transmit a message to
another actor configuration. The rule explicitly states, through the
environmental set
. Messages that cannot be delivered
locally, will be placed in the out-box of the sending actor. The out
reduction rule is used, at the sending side, to transmit a message to
another actor configuration. The rule explicitly states, through the
environmental set 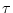 , that the
actor configuration should be in communication range with another actor
configuration that contains the target actor of the message. Then the
outgoing message will be removed from the out-box and placed in the
sent-box. This allows the actor to verify which messages have actually
been sent. Similar to the original model, the set of receptionists is
expanded with the local actor addresses that were communicated in the
message.
, that the
actor configuration should be in communication range with another actor
configuration that contains the target actor of the message. Then the
outgoing message will be removed from the out-box and placed in the
sent-box. This allows the actor to verify which messages have actually
been sent. Similar to the original model, the set of receptionists is
expanded with the local actor addresses that were communicated in the
message. 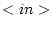 This rule is
called when an actor configuration receives a message from an external
actor that lives on another actor configuration that simulataneously
will be performing the rule with tag out.
In this situation, the message is placed in the in-box of the target
actor.
This rule is
called when an actor configuration receives a message from an external
actor that lives on another actor configuration that simulataneously
will be performing the rule with tag out.
In this situation, the message is placed in the in-box of the target
actor. 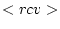 When a
message is available in the in-box of an actor, it can be received by
the actor. Once the message is being processed by the actor, the
message is moved to the rcv mailbox. This
means that an actor has a history of the messages that it processed.
This proves to be a useful session management utility as is shown in
the examples in section 4.
When a
message is available in the in-box of an actor, it can be received by
the actor. Once the message is being processed by the actor, the
message is moved to the rcv mailbox. This
means that an actor has a history of the messages that it processed.
This proves to be a useful session management utility as is shown in
the examples in section 4.
3.3.3 Mailbox Manipulation
3.3.4 Handling Environmental Contexts
Mobile applications used in an ad-hoc wireless network environment need to ``sense'' their physical environment. This ``sense'' is introduced in the model through the notion of first-class ``environmental context''. The first-class ``environmental context'' is supported with two reduction rules: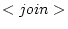 when two
actor configuration come in communication range. Every actor
when two
actor configuration come in communication range. Every actor 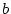 that requires a certain pattern
that requires a certain pattern 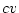 , which has become available in another
actor configuration
, which has become available in another
actor configuration 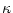 that is in communication range, will be informed of this by receiving a
``join'' message in its in-box. Also, for every matching pair of
required-provided patterns, the corresponding joined
mailbox is updated. In the joined mailbox,
a special kind of messages is stored, namely a resolution. A
resolution contains a) the kind of pattern (
that is in communication range, will be informed of this by receiving a
``join'' message in its in-box. Also, for every matching pair of
required-provided patterns, the corresponding joined
mailbox is updated. In the joined mailbox,
a special kind of messages is stored, namely a resolution. A
resolution contains a) the kind of pattern (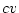 ) that has been matched and b) a provider
) that has been matched and b) a provider 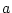 who provides the service.
who provides the service. 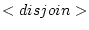 when two
actor configurations leave each others communication range. Every actor
that is aware of another joined actor, that has become unavailable,
will be informed of the disjoin. Once an actor is informed the
corresponding resolution is removed from the joined mailbox. Actors
that have removed the matching messages from their joined
mailbox will not be informed.
when two
actor configurations leave each others communication range. Every actor
that is aware of another joined actor, that has become unavailable,
will be informed of the disjoin. Once an actor is informed the
corresponding resolution is removed from the joined mailbox. Actors
that have removed the matching messages from their joined
mailbox will not be informed.
4 Examples
Now that we have defined the operational semantics of the extended actor model we show that it is useful in the context of ad-hoc wireless network environments by means of two examples. The examples are defined with actor code using the extended actor model from the previous section. The first example shows how anonymous communication can be expressed. In the second example we work out a meeting scheduler application for use in an ad-hoc wireless network environment.4.1 Pattern-Based Communication
We often want to send messages to an actor providing some service, but the actor address is unknown at the time of message sending, because the actor address depends on the physical environment of the embedded device. The anonymous actor can be described using type information [lKB02] or more semantic information about the service (such as a QoS property of the communication partner). In this example, we show how we can express such anonymous communication using the mailboxes in the extended actor model. We define a new communication primitive psend that takes two parameters: a description pattern of the required actor and the message that needs to be send.seq(add(required, pattern),
add(pending, msg))
The handleJoin definition walks over the resolutions in the joined mailbox. Each time a pattern that corresponds with the target of the messages in pending mailbox is found, the message is send to the provider of the pattern and removed from the pending mailbox.
if(join?(m),
for-each(
for-each(
if(eq?(target(msg), pattern(resolution)),
seq(send(provider(resolution), msg),
delete(pending, msg))),
messages(pending)),
messages(joined)))
Below is the definition of an actor that wants to print a file from the moment it comes into communication range of an actor that provides a printing service.
seq(psend('printer@300dpi, mkPrint(file)),
become(handleJoin(m)))
4.2 Meeting Scheduler
Suppose a group of people all walk around with a PDA that is equipped with a wireless transmitter. Each PDA has an agenda application running and the agenda can be used to schedule a meeting with a group of acquaintances. A request for a meeting can be made at any point of time (so the acquaintances do not have to be reachable at the point of requesting a meeting). We assume that the PDA's at some point in time will be in communication range. The owner of the PDA's does not have to be aware of the communication that goes on between the PDA's, so the PDA can become out of range at any point in the communication. The agenda application schedules a meeting in two steps:- try to make a reservation in the agenda from the participants of the meeting
- confirm the meeting in the agenda from the participant if all were successfully reserved.
4.2.1 Agenda Actor
The agenda is initialized with the e-mail address of the owner from the agenda. The e-mail address is used together with the type information of the application to join actor configurations together.seq(add(provided, mkProvided(email)),
become(
We have chosen to represent the agenda as a single slot that is available for meetings to reduce the length of our example. The slot has three states: free, reserved and confirmed. The agenda understands three messages:
- free: when this message is received and the slot is reserved then it becomes available for reservation. This message is used to undo a reservation.
- reserve: when this message is received and the slot is free, then the slot becomes reserved.
- confirm: when this message is received and the slot is reserved then the slot becomes confirmed.
The code below shows the implementation of the agenda. The function rec in the code calculates the fixed-point of a function [MT91] so that it can be called recursively.
if(free?(m),
become(b()))
if(reserve?(m),
seq(send(sender(m), mkReserveAnswer(session(m), #true)),
become(
if(and(free?(m), eq?(id, session(m))),
become(
if(reserve?(m),
seq(send(sender(m), mkReserveAnswer(session(m), #false)),
become(b(id))))
if(and(confirm?(m), eq?(id, session(m))),
become(
if(reserve?(m),
seq(send(sender(m), mkReserveAnswer(session(m), #false)),
become(b(id)))))
4.2.2 Scheduler Actor
The scheduler agent is responsible for contacting the agenda actors to schedule the meeting. In the scheduler actor definitions below we use three helper functions:- a filter function that uses a
predicate to filter elements in a list2
filter = rec(
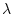 b.
b.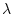 predicate.
predicate.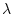 list.
list.
if(empty?(list),
emptyList,
if(predicate(car(list)),
cons(car(list), b(predicate, cdr(list))),
b(predicate, cdr(list)))))
- a map function that returns a transformed list and takes two parameters: a function that transforms elements and a list that is to be transformed is defined as in most standard Scheme implementations [ASS85].
- msend that allows to send a message
to a list of actor addresses or actors described with pattern
descriptions (such as in the previous example)
msend =
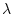 targets.
targets.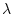 m.
m.
for-each(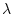 target.
target.
if(actorAddress?(target),
send(target, m),
psend(target, m)),
targets)
- madd that allows to add a list of
messages to a mailbox
madd =
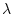 mbx.
mbx.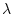 item.for-each(
item.for-each(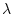 item.add(mbx,item), items)
item.add(mbx,item), items)
The scheduling agent is initialized as
![]() . The
scheduler agent has an id that is used to identify its session.
. The
scheduler agent has an id that is used to identify its session.
if(schedule?(m),
seq(madd(required,
map(
msend(participants(m), mkReserve(id)),
become(
if(and(reserveAnswer?(m), eq?(id, session(m))),
if(success?(m),
if(eq?( map(sender, filter(reserveAnswer?, messages(rcv))),
participants),
seq(msend(participants,mkConfirm(id)),
become(
seq(msend(map(destination, filter(reserve?, messages(sent))),
mkFree(id)),
mdelete(out,
map(identity, filter(reserve?, messages(out))),
send(customer, mkFailed()),
become(
When handling a reserveAnswer message we make use of the mailboxes introduced in our system:
- If the reservation was successful we check the box of received messages (named rcv) to see if we have received an answer from all the participants their agenda's. Due to the mailboxes there is no need to manually maintain the sessions. If all agenda's are successfully reserved, then the ScheduleAgent actor sends confirm messages to all Agenda's.
- If the reservation fails at some point we have to free up the agenda's of the reservations that were succesfull. We can use the mailbox of the messages that were sent (named sent) to track to which agenda actors we already sent out reservation request. To these actors we send the free message so that they can undo their reservation. We then delete the reservation messages that were not sent out from the mailbox out. We also notify the customer actor that sent the schedule message that the meeting could not be scheduled by sending it a failed message.
if(and(disjoin?(),
eq?( map(sender, filter(confirm?, messages(sent))),
participants))
seq(send(customer, mkSucceeded()),
become(
Each time the ScheduleAgent actor disjoins from an agenda actor it checks to see if all confirm messages were sent out, again using the mailbox sent. If all confirm messages were sent, then the customer actor that sent the schedule is notified with a succeeded message.
The second example shows that the mailboxes introduced in the extended actor model contain useful primitives that allow to structure the different conversations the scheduler has with the different agenda applications. It also shows the usefulness of the mailboxes ``sent'' and ``out'' to check and manipulate the communication status of different messages.
5 Related Work
5.1 Formalisms
Locality based linda [DFP97] is a formalisation of Linda [Gel85,CG89] (discussed below) but with the explicit notion of locations. Locations are added to the primitives of Linda, so the primitives work on a specific tuple space. Anonymous communication becomes impossible, because the location needs to be provided. In our context this would mean that the addresses of communicating devices need to be known, which is impossible to determine in ad-hoc wireless network environments. The model also does not define what happens with communication if the location is unavailable.
The mobile ambient calculus [CG00] expresses an abstraction between mobile computing and mobile computation in administrative domains. Mobile computation is the physical movement of devices between administrative domains, while mobile computing is the movement of a logical process (also called migration). The extended actor model and the ambient calculus are complementary. The mobile ambient calculus describes movement of processes between different locations and communication between ambients that are located in an ambient. The extended actor model describes how actors can structure their asynchronous communication to manage sessions and how new actors can be found in new physical environments. The mobile ambient calculus could be used to describe the physical movement of actor configurations.
5.2 Software Technology
JXTA [Gon01] is middleware for peer-to-peer environments and covers problems such as peer discovery and peer-to-peer communication. JXTA can also be employed in a wireless context [Gon02]. A disadvantage however is that wireless devices have to depend on JXTA relays in order to perform basic operations such as peer discovery. This means that JXTA relays have to be present in each physical environment before wireless devices are able to interact with one another. This is in conflict with the idea of transparency in pervasive computing.
Jini [AWO+99] enables discovery and lookup of services based on their description. It is possible to search for objects based on the object's type information and attributes. Jini is based on a central server architecture. A Jini server would have to be present in any place where devices need to find each other.
In [lKB02] a library is introduced to enable multicast and broadcast messages between objects in Java using wireless communication. Message delivery is based on the type information instead of addresses. The mechanism of sending messages based on type information is similar to our dynamic join that uses a pattern to find compatible devices. However, the lookup mechanism provided by the dynamic join in our extended actor model allows the use of other useful static information such as the e-mail address we used in the example of the meeting scheduler. This can simplify lookup of specific devices without having to know the exact actor address. Messages are also sent asynchronously in the library, but there is no notion of an outgoing queue. This means that if a message is sent and there is no device listening on the other side, then the message is lost. This means that checking message delivery is put on the shoulders of the developer, which will make the program inherently more complex.
Linda [Gel85,CG89] is a coordination language based on tuple spaces. There are several primitives that make communication explicit in the code. There is a primitive for putting values in the tuple space (asynchronous) and primitives for getting values from the tuple space (blocking). Tuple spaces are interesting, because they allow communication without the need to specify the communication address of the receiver, much like in the spirit of our join rule. Linda is based on a central server architecture, there is one central tuple space where the structured values are put, which makes it not suitable for ad-hoc wireless network environments. The language does not provide semantics of communication failures in the language, which is important in our context.
6 Conclusion
In this paper we extended the operational semantics of the actor model in order to deal with three problems associated with ad-hoc wireless network environments:- How do several devices find each other?
To handle this problem we introduced reduction rules join and disjoin that define what happens when devices come in communication range of one another. - How to deal with communication failures and disconnected
operation?
This problem is handled with the introduction of the in, rcv, out and sent mailboxes that allow us to track and intervene in the communication between different devices. - How to keep track of different conversations that occur in
different places?
This problem is handled through the custom manipulation of mailboxes.
Acknowledgements
Thanks to Thomas Cleenewerck for proof-reading this paper and for providing us with some useful hints to increase the readability of this paper.Bibliography
-
- Agh90
- Gul Agha.
Concurrent object-oriented programming.
Communications of the ACM, 33(9):125-141, 1990. - AMST97
- Gul Agha, Ian A. Mason, Scott F. Smith, and
Carolyn L. Talcott.
A foundation for actor computation.
Journal of Functional Programming, 7(1):1-72, 1997. - ASS85
- H. Abelson, G. J. Sussman, and J. Sussman.
Structure and Interpretation.
MIT Press, Cambridge, MA, 1985. - AWO+99
- Ken Arnold, Ann Wollrath, Bryan O'Sullivan, Robert Scheifler, and
Jim Waldo.
The Jini specification.
Addison-Wesley, Reading, MA, USA, 1999. - CG89
- Nicholas Carriero and David Gelernter.
Linda in context.
Commun. ACM, 32(4):444-458, 1989. - CG00
- Luca Cardelli and Andrew D. Gordon.
Mobile ambients.
In Andrew Gordon, Andrew Pitts, and Carolyn Talcott, editors, Electronic Notes in Theoretical Computer Science, volume 10. Elsevier, 2000. - Chu85
- A. Church.
The Calculi of Lambda-Conversion, volume 6 of Annals of Mathematical Studies.
Princeton University Press, Princeton, 1985. - DFP97
- R. De Nicola, G. Ferrari, and R. Pugliese.
Locality based Linda: Programming with explicit localities.
Lecture Notes in Computer Science, 1214:712-??, 1997. - FGL+96
- C. Fournet, G. Gonthier, J. J. Levy,
L. Maranget, and D. Remy.
A Calculus of Mobile Agents.
In U. Montanari and V. Sassone, editors, Proceedings of 7th International Conference on Concurrency Theory (CONCUR'96), volume 1119 of LNCS, pages 406-421. Springer-Verlag, Berlin, Germany, August 1996. - Gel85
- David Gelernter.
Generative communication in Linda.
ACM Transactions on Programming Languages and Systems, 7(1):80-112, January 1985. - Gon01
- Li Gong.
Project jxta: A technology overview.
Technical report, SUN Microsystems, http://www.jxta.org/project/www/docs/TechOverview.pdf, 2001. - Gon02
- Li Gong.
Jxta for j2me Ð extending the reach of wireless with jxta technology.
Technical report, SUN Microsystems, http://www.jxta.org/project/www/docs/JXTA4J2ME.pdf, 2002. - KS90
- K. Kahn and Vijay A. Saraswat.
Actors as a special case of concurrent constraint (logic) programming.
In Proceedings of the European conference on object-oriented programming on Object-oriented programming systems, languages, and applications, pages 57-66. ACM Press, 1990. - lKB02
- lan Kaminsky and Hans-Peter Bischof.
Many-to-many invocation: A new object oriented paradigm for ad hoc collaborative systems.
17th Annual ACM Conference on Object Oriented Programming Systems, Languages, and Applications (OOPSLA 2002), 2002. - MT91
- Ian Mason and Carolyn Talcott.
Equivalence in functional languages with effects.
Journal of Functional Programming, 1(3):287-328, July 1991.
Footnotes
- ... list2
- In the
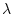 calculus a
pair is created with the function cons.
The function car returns the first element
of the pair, while the cdr function
returns the second element. A list of elements is represented as a
nesting of pairs. e.g. (1, 2, 3) is represented as (1, (2, (3, '())))
calculus a
pair is created with the function cons.
The function car returns the first element
of the pair, while the cdr function
returns the second element. A list of elements is represented as a
nesting of pairs. e.g. (1, 2, 3) is represented as (1, (2, (3, '())))
| http://werner.yellowcouch.org/ werner@yellowcouch.org |  |