| Home | Papers | Reports | Projects | Code Fragments | Dissertations | Presentations | Posters | Proposals | Lectures given | Course notes |
|
|
Using Genetic Programming to Generate Protocol Adaptors for Interprocess CommunicationWerner Van Belle1* - werner@yellowcouch.org, werner.van.belle@gmail.com Abstract : As mobile devices become more powerful, interprocess communication becomes increasingly more important. Unfortunately, this larger freedom of mobility gives rise to unknown environments. In these environments, processes that want to communicate with each other will be unable to do so because of protocol conflicts. Although conflicting protocols can be remedied by using adaptors, the number of possible combinations of different protocols increases dramatically. Therefore we propose a technique to generate protocol adaptors automatically. This is realised by means of genetically engineered classifier systems that use Petri nets as a specification for the underlying protocols. This paper reports on an experiment that validates this approach.
Keywords:
mobile agents, interface conflicts, peer-to-peer computing, genetic algorithms, classifier systems |
1 Introduction
In the field of evolvable computing, software (and hardware) is developed that adapts itself to new runtime environments as necessary. The runtime environments targetted in this paper are open distributed systems in which interprocess communication forms an essential problem. In these environments an application consists of processes that communicate with other processes to reach specific goals.
With the advent of mobile devices these processes do not necessarily know in which kind of runtime environments they will execute. Therefore they rely on standardised solutions, such as JINI, to find other processes offering a certain behaviour.
Once the other process is known, the real problems start. How can the requesting process communicate with the unknown offered process ? Given the fact that those processes are developed by different organisations, the protocols provided and required can vary greatly. As a result protocol conflicts arise.
On first sight, a solution to this problem would be to offer protocol adaptors between every possible pair of processes. The problem with this approach is that the number of adaptors grows quadratic to the number of process protocols and as such it simply doesn't scale. The solution is to automate the generation of protocol adaptors between communicating processes.
As a potentially useful technique for this adaptor generation, we explored the research domain of adaptive systems. We found that the combination of genetic programming, classifier systems, and a formal specification in terms of Petri nets allowed us to automate the detection of protocol conflicts, as well as the creation of program code for adaptors that solve these conflicts. This paper reports on an experiment we performed to validate this claim.
2 Prerequisites of Interprocess Communication
Processes communicate with each other only by sending messages
over a communication channel (similarily to CSP [1]
and the ![]() -calculus [2]). Communication channels
are accessed by the process' ports. Processes communicate
asynchronously and always copy their messages completely upon
sending. The connections between processes are full duplex: every
process can send and receive
messages over a port.
This brings us in a situation where a process provides
a
certain protocol and requires a protocol
from another
process. A process can have multiple communication channels: for
every communication partner and for every provided/required
protocol.
-calculus [2]). Communication channels
are accessed by the process' ports. Processes communicate
asynchronously and always copy their messages completely upon
sending. The connections between processes are full duplex: every
process can send and receive
messages over a port.
This brings us in a situation where a process provides
a
certain protocol and requires a protocol
from another
process. A process can have multiple communication channels: for
every communication partner and for every provided/required
protocol.
We imposed other requirements on the interprocess communication to allow us to generate adaptors:
- Implicit addressing. No process can use an explicit address of another process. Processes work in a connection-oriented way. The connections are set up solely by one process: the connection broker. This connection broker will also evolve adaptors and place them upon the connections when necessary.
- Disciplined communication. No process can communicate with other processes by other means than its ports. Otherwise, `hidden' communication (e.g., over a shared memory) cannot be modified by the adaptor. This also means that all messages passed over a connection should be copied. Messages cannot be shared by processes (even if they are on the same host), because this would result in a massive amount of concurrency problems.
- Explicit protocol descriptions. While humans prefer a protocol description written in natural language, computers need an explicit formal description of the protocol semantics. A simple syntactic description is no longer suitable.
3 Specifying Protocols
As a running example we choose a typical problem of communicating processes: how processes synchronise with each other. Typically, a server provides a concurrency protocol (often a transaction protocol) [3] that can be used by clients. The clients have to adhere to this specification or they won't function. Since the clients also expects a certain concurrency behaviour from the server, it is possible that the required interface and provided interface differ.
For example, a client/server can require/provide a full-fledged optimal transaction protocol or it can require/provide a simple locking protocol. When two such protocols of a different kind interact, we can run into an incompatibility problem.
In our example we use a simple locking protocol of the server with which a client can typically lock a resource and then use it. The API for the server is described as follows. (A similar protocol description can be given for the clients.)
-
- incoming lock(resource)
outgoing lock_true(resource)
outgoing lock_false(resource)
// lock_true or lock_false are sent back whenever a lock
// request comes in: lock_true when the resource is locked,
// lock_false when the resource couldn't be locked.
incoming unlock(resource)
outgoing unlock_done(resource)
// will unlock the resource. Send unlock_done back when done.
incoming act(resource)
outgoing act_done(resource)
// will do some action on the process.
The semantics of this protocol can be implemented in different ways. We will use two kinds of locking semantics [3]:
Counting semaphores allow a client to lock a resource multiple times. Every time the resource is locked the lock counter is increased. If the resource is unlocked the lock counter is decreased. The resource is finally unlocked when the counter reaches zero.
Binary semaphores provide a locking semantics that doesn't offer a counter. It simply remembers who has locked a resource and doesn't allow a second lock. When unlocked, the resource becomes available again.
Differences in how the API considers lock and unlock can give rise to protocol conflicts. In figure 1 the client process expects a counting semaphore from the server process, but the server process offers a binary semaphore. The client can lock a resource twice and expects that the resource can be unlocked twice. In practice the server just marked the resource as locked. If the client unlocks the resource, the resource will be unlocked. Acting upon the server now is impossible, while the client expects it to be possible.
This protocol conflict arises because the API does not specify enough semantic information. Hence, we propose to use a more detailed and generally applicable formalism, namely Petri nets, to offer an explicit description of the protocol semantics. Petri nets [4] offer a model in which multiple processes traverse states by means of state transitions.
In the context of our locking example, this allows us to write a suitable adaptor by relying on: (1) which state the client process expects the server to be in; (2) in which state the server process is. Both kinds of information are essential: If we don't know that the client thinks that it still has a lock, and we don't know that the state of the server is unlocked (see figure 1), no learned algorithm can make a correct decision.
![\includegraphics[width=1.0\textwidth, keepaspectratio]{CombinedLocking}](img3.png) |
As an example Petri net that offers the needed semantics, the left part of figure 2 specifies a binary semaphore locking strategy. The current state is unlocked. From this state the process requiring this protocol, can choose only one action: lock. It then goes to the locking state until lock_true or lock_false comes back. We can also use this Petri net to model the behaviour of a process that provides this protocol. It is perfectly possible to offer an protocol that adheres to this specification, in which case, the incoming lock is initiated from the client, and lock_true or lock_false is sent back to the client when making the transition.
4 Evolving Protocols
Protocol adaptors overcome the semantic differences between two processes. We propose to use a genetic algorithms [5] with classifier systems to generate adaptors. Classifier systems are known to work very well in cooperation with genetic algorithms, they are Turing complete and they are symbolic. This is important because our Petri net description is in essence a symbolic representation of the different states in which a process can reside.
If this representation would be numerical, techniques such as neural networks [6], reinforcement learning and Q-learning [7] could probably be used.
The standard questions before implementing any genetic programming technique are: What are the individuals and their genes? How do we represent the individuals? How do we define and measure the fitness of an individual? How do we initially create individuals? How do we mutate them and how do we create a cross-over of two individuals? How do we compute a new generation from an existing one? For a quick overview of the parameters of our genetic program we refer to table 4.
In our implementation, the individuals will be protocol adaptors between communicating processes. The question of how to represent these individuals is more difficult. We could use well-known programming languages to represent the behaviour of the adaptor. Unfortunately, the inevitable syntactic structure imposed by these languages complicates the random generation of programs. Moreover, these programming languages do not offer a uniform way to access memory.
An alternative that is more suitable for our purposes is the Turing complete formalism of classifier systems [5]. A classifier system is a kind of control system that has an input interface, a finite message list, a classifier list and an output interface. The input and output interface put and get messages to and from the classifier list. The classifier list takes a message list as input and produces a new message list as output. Every message in the message list is a fixed-length binary string that is matched against a set of classifier rules. A classifier rule contains a number of (possibly negated) conditions and an action. These conditions and actions form the genes of each individual in our genetic algorithm. Conditions and actions are both ternary strings (of 0, 1 and #). `#' is a pass-through character that, in a condition, means `either 0 or 1 matches'. If found in an action, we simply replace it with the character from the original message. Table 1 shows a very simple example. When evaluating a classifier system, all rules are checked (possibly in parallel) with all available input messages. The result of every classifier evaluation is added to the end result. This result is the output message list. For more details, we refer to [5].
Input message list = { 001, 101, 110, 100 }
Output message list = { 111, 100, 110 } |
A classifier system needs to reason about the actions to be
performed based on the available input. In our implementation, the
rules of a classifier system consist of a ternary string
representation of the client state and server state (as specified
by the Petri net), as well as a ternary string representing the
requested Petri net transition from either the client process or
the server process. With these semantics for
the classifier rules, translating a request from the client to the
server requires only one rule. Another rule is needed to translate
requests from the server to the client (see table 2).
The number of bits needed to represent the transitions depends on the number of possible state transitions in the two Petri nets of figure 2. The number of bits needed to represent the states of each Petri net depends on the number of states in the Petri net as well as the variables that are stored in the Petri net (e.g., the lockcount variable requires 2 bits if we want to store 4 levels of locking).
|
|||||||||||||||||||||||||||||||||||
Although this is a simple example, more difficult actions can be represented. Consider the situation where the client uses a counting-semaphores locking strategy and the server uses a binary-semaphores locking strategy. In such a situation we don't want to send out the lock-request to the server if the lock count is larger than zero. Table 3 shows how we can represent such a behaviour.
|
|||||||||||||||||||||||||||||||||||
The genetic programming we implemented uses a full classifier list with variable length. The classifier list is an encoding of the Petri nets, as representation for the individuals. Every individual is initially empty. Every time an individual encounters a situation where there is no matching gene a new gene (i.e., a new classifier rule) will be added with a condition that covers this situation and a random action that is performed on the server and/or the client. This way of working, together with the use of Petri nets guarantees that the genetic algorithm will only search within the subspace of possible solutions. Without these boundaries the genetic algorithm would take much longer to find a solution.
Fitness of an individual is measured by means of a number of test scenarios. Every test scenario illustrates a typical behaviour the client requests from the server. The fitness of an individual is determined by how many actions the scenario can execute without yielding unexpected behaviour. Of course this is not enough; we should not have solutions that completely shortcut the server. For example, the algorithm could return lock_true every time a request comes in from the client, without even contacting the server. To avoid this kind of behaviour our algorithm provides a covert channel that is used by the test scenario to contact the server to verify its actions.
The genetic
programming uses a steady-state GA, with a ranking selection
criterion: to compute a new generation of individuals, we keep (reproduce)
10% of the individuals with the best fitness. We throw away 10%
of the worst individuals (not fit enough) and add cross-overs
from the 10% best group. To create a
cross-over of individuals we iterate over
both classifier
lists and each time randomly select a rule that will be stored in
the resulting individual. It should be noted that the individuals
that take part in cross-over are never mutated. The remaining 80%
of individuals are mutated, which means
that the genes of
each individual are changed at random: for every rule, a new
arbitrary action to be performed on server or client is chosen. On
top of this, in 50% of the classifier rules, one bit of the
client and server state representations is generalised by
replacing it with a #. This allows the genetic program to find
solutions for problems that are not presented yet.
|
5 The Experiment
We will now present the experiment that shows the feasibility of the above techniques to automatically learn an adaptor between incompatible locking strategies.
The experiment is set up as a connection broker between two processes. The first process contacts the second by means of the broker. Before the broker sets up the connection it will generate an adaptor between the two parties to mediate semantic differences. It does so by requesting a running test process from both parties. The client will produce a test client and test scenarios. The server will produce a test server. In comparison with the original process, these testing processes have an extra testing port, over which we can reset them. Furthermore, this testing port is also used as the covert channel for validating actions at the server.
The genetic program, using a set of 100 individuals (i.e., adaptor processes), will deploy the test processes to measure the fitness of a particular classifier system. Only when a perfect solution is reached, i.e., a correct adaptor has been found, the connection is set up. For reliability reasons we have repeated the experiment (i.e., the execution of the genetic program) 100 times.
The scenarios offered by the client are the ones that determine what kind of classifier system is generated. We have tried this with three scenarios, as illustrated on the left of figure 3. Scenario 1 is a sequence: [lock(), act(), unlock()]. Scenario 2 is the case we explained in figure 1. Scenario 3 is similar to scenario 1: [lock(), act(), act(), unlock()]. The reason why we added such a look-alike scenario will become clear in our observations. In all three scenarios, we issue the same list of messages three times to ensure that the resource is unlocked after the last unlock operation.
![\includegraphics[ width=1.0\textwidth]{ScenariosCombined2}](img4.png)
|
1 Observations
An examination of the results of several runs of our genetic programming algorithm lead to the following observations:
When we used the covert channel to measure the fitness, we found that (for all 100 runs of the GA) a perfect solution was found within at most 11 generations. When we didn't use the covert channel to check the actions at the server side, the genetic algorithm often (30%) created a classifier that doesn't even communicate with the server. In such a situation the classifier immediately responds lock_true whenever the client requests a lock.
Occasionally a classifier system was generated with a strange behaviour. Its fitness was 100%, but it worked asynchronously. In other words, the adaptor would contact the server process before the client process even requested an action from the server process. It could do so because the adaptor knew that the client would request that particular action in the given context. This is illustrated on the right of Figure 3. It implies that a learned algorithm can anticipate certain kinds of future behaviour.
Initially, we only used scenario 1 and 2 to measure the fitness of each individual. We encountered the problem that sometimes, the adaptor anticipates too much and after the first act, keeps on acting. This problem was solved by assigning a zero fitness to such solutions.
As a last
experiment we measured the fitness by combining
information from all three scenarios. This allowed the genetic
algorithm to find a perfect solution with less generations because
separate individuals that developed behaviour for a specific test
scenario were combined in a later generation using cross-over.
This illustrates the necessity for a cross-over operator. A random
search would take considerably more time to find a combination of
both behaviours.
One of the classifier system that is generated by the genetic algorithm, when providing as input all three test scenarios, is given in table 5. The produced classifier system simply translates calls from client to server and vice versa, unless it is about a lock call that should not be made since the server is already locked. The bit patterns in the example differ slightly from the bit patterns explained earlier. This is because we need the ability to make a distinction between a 'transition-message' and a 'state-message'. All transition messages start with 00 and all state-messages start with 10 for client-states and 11 for server-states.
|
2 Discussion
In our approach, the problem of 'writing correct adaptors' is shifted to the problem of 'specifying correct test sets': whenever the developer of a process encounters an incompatibility, he needs to specify a new test scenario that avoids this behaviour. This test scenario is given as additional input to the genetic algorithm, so that the algorithm can find a solution that avoids this incompatibility. The result of this approach is that the programmer does not have to implement the adaptors directly, but instead has the responsibility of writing good test sets (i.e., a consistent set of scenarios that is as complete as possible). This is a nontrivial problem, since the test set needs to cover all explicit as well as implicit requirements. The main advantage of test sets over explicit adaptors is that we would need a new adaptor for every pair of communicating processes, while we only need one test set for each individual process. As such, test sets are more robust to changes in the environment: when a process needs to communicate with a new process, there is a good chance that the test set will already take into account potential protocol conflicts. Another important advantage of test sets is that they can help in automatic program verification. Bugs in the formal specification (the Petri net) can be detected and verified at runtime. As such, this approach helps the developer to stay conform to the program specification. This clearly helps him in his goal to write better software.
Below we discuss some strengths and weaknesses of our approach:
Automatically generated adaptors can be better than hand-crafted adapters since they can reorder incoming and outgoing messages as necessary. This can result in anticipated behaviour that boosts performance.
The genetic algorithm we proposed has the problem that it needs to learn a certain behaviour based on a very small set of examples. Therefore, the learning algorithm will automatically generate more general or more specific adaptors when offered test sets. This tendency to generalize matches does not always correspond to how a programmer tries to generalise. If there is a close correspondence, the programmer simply needs to write test sets that will naturally be generalised to the desired adaptor. On the other hand, if the generalisation (or specialisation) does not fit the developer's way of thinking, the algorithm will generate seemingly illogical adaptors.
An ideal test scenario should cover all the actions that will be invoked upon the server in all possible combinations. How can we write good tests that do not leave any open holes for the programmer? And if we can write such tests, are the Petri nets still necessary? In other words, is it possible to learn the adaptor automatically just by looking at the interaction between the processes?
Some protocol
conflicts that seem simple at first sight cannot be
solved (not even by humans). For example, the locking protocol example
could be used to lock simple ![]() - specified cells on a checker board.
It is impossible to protocol this with a locking strategy that locks
and unlocks the whole board at once. A simple solution such as `lock
all fields' will not work because other communication partners can
enter the field and lock a single position. This indicates that the
approach presented here is good in solving `control flow' problems
but is bad at converting `data representations'. However, this is
a general AI problem [11] for
which no solution yet
has been found.
- specified cells on a checker board.
It is impossible to protocol this with a locking strategy that locks
and unlocks the whole board at once. A simple solution such as `lock
all fields' will not work because other communication partners can
enter the field and lock a single position. This indicates that the
approach presented here is good in solving `control flow' problems
but is bad at converting `data representations'. However, this is
a general AI problem [11] for
which no solution yet
has been found.
In this paper we presented only a simple example with small protocols (binary versus counting semaphore locking strategies) for the sake of the presentation. We are currently investigating how we can write adaptors by generating a suitable petri-net instead of a classifier system. More elaborate experiments and technical details can be found on http://borg.rave.org/adaptors/.
6 Conclusion
We proposed an automated approach to create intelligent protocol adaptors to resolve incompatibilities between communicating processes. Such an approach is indispensable to cope with the combinatorial explosion of protocol adaptors that are needed in an open distributed setting where processes interact with other processes in unpredictable ways.
Our approach uses a genetic programming tecnique that evolves classifier systems. These classifier systems contain classifiers that react upon the context they receive from both client process and server process. The context is defined as a combination of the possible client-side and server-side states as given by a user-specified Petri net. To measure the fitness of an adaptor, the user needs to provide test scenarios as input. This enables the user to avoid undesired behaviour in interprocess communication.
Acknowledgements
Thanks to Johan Fabry, Tom Lenaerts, Anne Defaweux, Tom Tourwé and the anonymous referees for reviewing this paper.
Bibliography
- 1- Hoare, C.:
- Communicating Sequential Processes.
International Series in Computer Science. Prentice Hall (1985) - 2- Milner, R.:
- Communicating and Mobile Systems: the
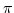 -calculus.
-calculus.
Cambridge University Press (1999) - 3- Lea, D.:
- Concurrent Programming in Java (2nd edition) Design Principles
and Patterns.
The Java Series. Addison Wesley (2000) - 4- Reisig, W.:
- An Informal Introduction To Petri Nets.
Proc. Int'l Conf. Application and Theory of Petri Nets, Aarhus, Denmark (2000) - 5- Glodberg, D.E.:
- Genetic Algorithms in Search, Optimization, and Machine Learning.
Addison-Wesley (1989) - 6- Kröse, B., van der Smagt,
P.:
- An introduction to neural networks.
University of Amsterdam (1996) - 7- Sutton, R.S., Barto, A.G.:
- Reinforcement Learning - An Introduction.
MIT Press (1998) - 8- Smith, S.:
- A Learning System Based on Genetic Adaptive Algorithms.
PhD thesis, Department of Computer Science, University of Pittsburgh (1980) - 9- Bull, L., Fogarty, T.:
- Co-evolving communicating classifier systems for tracking.
Proc. Int'l Conf. Neural Networks and Genetic Algoriths (1993) - 10- Koza, J.R.:
- Genetic Programming; on the programming of computers by means of
natural selection.
MIT Press (1992) - 11 - Morgenstern, L.:
- The problem with solutions to the frame problem.
In Ford, K.M., Pylyshyn, Z., eds.: The Robot's Dilemma Revisited: The Frame Problem in Artificial Intelligence.
Ablex Publishing Co., Norwood, New Jersey (1996) 99-133
Footnotes
- ... Belle
- Corresponding author. He is developing peer-to-peer embedded systems for a project funded by the Flemish Institute for Science and Technology (IWT).
- ... Mens
- Tom Mens is a Postdoctoral Fellow of the Fund for Scientific Research - Flanders (Belgium)
- ... process.
- Currently we are investigating whether we can drop this translation and generate an adaptor from the Petri net representation directly.
- ...BlindTranslation).
- This method of using full classifier systems as individuals is known as the Pittsburgh approach [8]. The Michigan approach, whereby a set of classifier rules evolve together to reach a solution[9], is not suitable for our purposes because one rule doesn't cover the behaviour of an adaptor. As such, cross-over between single rules would not help that much.
- ... group
- These values were taken from [10] and gave good results during our experiments.
| http://werner.yellowcouch.org/ werner@yellowcouch.org |  |
![\includegraphics[width=6cm]{SimpleConflict}](img2.png)