Subsections
8. Module 1: The Enforce-Action Module
Figure 8.1:
Bypassing a concurrency interface
|
|
IN CHAPTER we have explained that we will
construct an adaptor based on three requirements. Every requirement
will be satisfied by one module. The enforce-action module will allow
the adaptor to satisfy the no-conflict requirement. To this end, this
module will bypass a provided concurrency interface by means of a
logic deduction. Therefore a reachability analysis of the Petri-net
description of the provided concurrency interface will be used. In
this chapter, after presenting standard techniques to do such an analysis,
we will explain how we will perform a reachability analysis by means
of prolog.
A REQUIREMENT FOR THE MODULE we will develop is that it should
be able to receive any possible action from the logic interface
and execute it on a server component. To do so the necessary synchronization
messages should be generated automatically.
The adaptor itself has 3 ports (see picture 8.1).
One port is connected to the concurrency module and provides/requires
a logic interface. Another port is connected to the server-component
and provides/requires a logic interface and a last port, providing/requiring
a synchronization interface also connected to the server component.
In essence, there are two completely different techniques which we
can use to shortcut the concurrency strategy. The first is the use
of an on-line learning algorithm, which is suitable in this case because
the learning algorithm can keep on trying to enable a certain action
until it is successful. In the meantime the concurrency adaptor can
be set to wait. The reward given here is straightforward and defined
by the enabling of the required transition.
The second approach uses inductive reasoning to deduce what kind of
actions should be taken in a certain context. This is the approach
we will investigate in more detail because it has a faster response
and works in most situations.
DEDUCING HOW WE CAN ENABLE a certain state within a petri-net,
given its current marking seems typically a problem of reachability,
however there are some differences. A reachability analysis of a Petri-net
indicates whether we can reach a certain marking or not, often information
is included how this marking can be reached. In our case we don't
want to reach a specific marking, we only want to know how to enable
a transition as a result of a certain marking. Formally, we want to
find a way how to reach
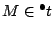 from
from 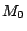 .
.
Nevertheless, in general formal reachability analysis not only gives
a yes or no answer to the reachability question, but also gives a
way to reach the target marking. Since we have a set of target markings
(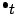 ), which we want to reach, we investigate the use of
these formal techniques. Reachability is decidable [EN94].
However it might take a long time. Generally, it can be solved in
exponential time. However for a lot of Petri-net classes different
results exist. For instance:
), which we want to reach, we investigate the use of
these formal techniques. Reachability is decidable [EN94].
However it might take a long time. Generally, it can be solved in
exponential time. However for a lot of Petri-net classes different
results exist. For instance:
- If the petri-net is symmetric then the reachability problem
is EXPTIME-complete (see glossary). A petri-net is symmetric when
for every transition
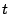 there is a transition
there is a transition 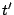 that undoes
the effect of the first transition and returns to the original marking.
This is a property which is often found in concurrency interfaces.
Once a lock is obtained it is possible to release it again. However,
aside from this intuition nothing guarantees that the petri-net also
exhibits this behavior.
that undoes
the effect of the first transition and returns to the original marking.
This is a property which is often found in concurrency interfaces.
Once a lock is obtained it is possible to release it again. However,
aside from this intuition nothing guarantees that the petri-net also
exhibits this behavior.
- If the petri-net is conflict-free and bounded
then reachability is decidable in P. (see glossary) A Petri-net is
bounded when there is a maximum number of possible tokens present
at a certain place (see section 3.10).
A Petri-net is conflict-free if for every possible marking the net
is persistent. A petri-net is persistent if for every place with more
than one enabled output transition, the execution of one transition
does not disable the other transition. In the case of concurrency
interfaces this is highly likely because normally multiple transitions
will not be enabled at once and the amount of resources remains fixed.
- Reachability in timed petri-nets is NP-complete [LLPY97,BP96]).
Extensions to Petri-nets may complicate these results. For instance:
- Our expression language is not a standard language so we don't exactly
know whether all these properties hold with the given language. We
assume they do, because the expression language used is a functional
language which is not Turing complete and as we will experimentally
observe most concurrency strategies can be written down as finite
state machines.
- Colored petri-nets make all these formal approaches a bit problematic.
Expanding a colored Petri-net to a simple Petri-net may require an
infinite explosion, so all these decidability criteria need to be
investigated again.
There are a number of algorithms available to decide whether a marking
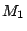 is reachable from an initial marking
is reachable from an initial marking 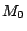 . Below we will
briefly summarize them and explain why they do not fit our needs.
. Below we will
briefly summarize them and explain why they do not fit our needs.
- Reachability graphs: The reachability of marking
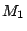 from
marking
from
marking 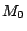 is often decided by creating a reachability-graph.
Here the nodes of the graph contain a marking and the arcs contain
the transition that brings one from marking a to marking b. Reachability
is then decided by creating a matrix containing on the X/Y-axis all
possible nodes/markings. The values within the matrix specify whether
X is reachable from Y. With every step more positions are filled with
1, by taking the transitive closure of the reachability graph. This
approach is formally very nice; a drawback however is that it takes
too much time since often we only want to know whether A is reachable
from B and not whether all possible A 's are reachable from all possible
B 's.
is often decided by creating a reachability-graph.
Here the nodes of the graph contain a marking and the arcs contain
the transition that brings one from marking a to marking b. Reachability
is then decided by creating a matrix containing on the X/Y-axis all
possible nodes/markings. The values within the matrix specify whether
X is reachable from Y. With every step more positions are filled with
1, by taking the transitive closure of the reachability graph. This
approach is formally very nice; a drawback however is that it takes
too much time since often we only want to know whether A is reachable
from B and not whether all possible A 's are reachable from all possible
B 's.
- Unfolding Petri-nets: With this approach a Petri-net is unfolded
into another Petri-net, usually with an infinite but simpler structure.
McMillan [ERV96], proposed an algorithm for the
construction of a finite initial prefix of the Petri-net, which contains
full reachability information. However, this information is difficult
to generate, and can take a long time. Therefore we didn't investigate
this track further.
- Exploiting symmetry: It is possible to exploit symmetry between
states by only looking at one side of the symmetry. This is especially
useful for colored Petri-nets. Intuitively: within a dining philosopher
Petri-net, there is a 4 way symmetry. There is no need in trying out
every philosopher, which reduces the state explosion drastically.
How this is done in practice is described in detail in [Jør].
Aside from all these techniques, there is a property of our problem
which might also be exploited. In our case, we have the ability to
search for a specific solution. As stated earlier, we want to know
how to get from a certain marking 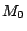 to another certain marking
to another certain marking
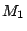 , that enables transition
, that enables transition 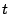 . It is important that
we are not even looking for the shortest path, but simply need to
find one way to enable
. It is important that
we are not even looking for the shortest path, but simply need to
find one way to enable 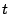 .
.
Now, let us turn back our attention to Petri-nets. As explained in
section 3.4.4, it is difficult to create
a high performance Petri-net evaluator for colored Petri-nets because
a transition is enabled if a suitable combination of input
tokens exist. This is typically a search problem and we have argued
that a logic engine (such as prolog) might be a suitable language
to write a Petri-net evaluator in. Given the fact that most reachability
analysis work for elementary Petri-nets, but have often difficulties
understanding the possible expressions present in colored Petri-nets,
it seems appropriate to use prolog as a logic engine to do a reachability
analysis. This is what we will describe below.
8.3 Converting a Petri-Net Description to
Prolog Rules
BEFORE WE CAN DEDUCE certain interesting properties from
a Petri-net we need some representation of Petri-nets within prolog.
We will now explain how we can convert Petri-nets to prolog rules.
But before we do so, we will explain how we define our markings.
![\begin{algorithm}
% latex2html id marker 4170
[!htp]
\begin{list}{}{
\setlengt...
....}{\small\par
}\end{list}\par
\caption{
Definition of markings.}
\end{algorithm}](img314.png)
Markings are declared by a set of simple rules as shown in algorithm
18. A marking is represented as an association
list of place-names and place-content. The content of a place is a
list of tokens. The basic operations on markings are del_marking(input_marking, to_delete, output_marking)
and add_marking(input_marking, to_add, output_marking).
del_marking will remove a token from an input marking
and create an output marking.
add_marking will add
a token to a given marking. Markings can be either relative or absolute.
A marking is relative if it only mentions the necessary
tokens without including all possible other tokens that could also
be present. A marking is absolute if all the tokens that are
available are specified in the marking. The notion of a relative and
absolute marking is necessary to be able to deduce which tokens should
be present in a certain marking without actually having a real marking
at hand. Without the notion of a relative marking the process of finding
out how to reach a certain sub-marking might take a long time because
the step predicates would try out all possible permutations within
the offered absolute marking. A relative marking is well defined because
Petri-nets do not allow an absence check of tokens, so we do not need
to specify which tokens cannot be in a certain marking.
![\begin{algorithm}
% latex2html id marker 4210
[!htp]
\begin{list}{}{
\setlengt...
...l\tt step} is defined
for the {\small\tt lock(X,Y)} transition.}
\end{algorithm}](img315.png)
The convention we will use is that step(T,M,N) declares
a valid transition 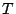 which brings marking
which brings marking 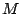 to marking
to marking 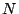 .
E.g., step(lock(X,Y),[],N) will find all possible resulting
markings N after executing the lock(X,Y) transition.
This is illustrated in algorithm 19. Depending
on whether M, N or T are known the behavior is different.
.
E.g., step(lock(X,Y),[],N) will find all possible resulting
markings N after executing the lock(X,Y) transition.
This is illustrated in algorithm 19. Depending
on whether M, N or T are known the behavior is different.
- If both
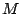 and
and 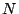 are known, the predicate step(T,M,N) will check
whether
are known, the predicate step(T,M,N) will check
whether 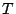 is a valid transition between M and N. This is done by
verifying the presence of all input tokens in M and the presence of
all required output tokens in N.
is a valid transition between M and N. This is done by
verifying the presence of all input tokens in M and the presence of
all required output tokens in N.
- If only
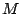 is known,
is known, 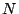 will match the resulting output. If multiple
token-pulls are possible from M, multiple answers will be placed in
will match the resulting output. If multiple
token-pulls are possible from M, multiple answers will be placed in
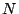 .
.
- If only
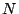 is known,
is known, 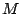 will match the necessary input for T to
result in N. If multiple possible inputs are possible they will all
match.
will match the necessary input for T to
result in N. If multiple possible inputs are possible they will all
match.
- If neither
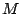 nor
nor 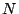 is known, The transition will create a relative
marking
is known, The transition will create a relative
marking 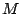 and
and 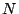 .
.
Together with definitions for steps and markings we need a way to
categorize transitions, places, incoming transition, outgoing transitions,
synchronization actions, logic actions and other. These categories
are simply declared as facts. They are:
- transition: declares whether something is a transition.
- place: declares whether something is a place.
- action: an action is a message that can be received or sent
over a logic interface. These are return_joinactor(_),
set_position(_,_,_), return_set_position, isfree(_,_),
return_free_true and return_free_false.
- synchro: a synchronization message. Every transition that
is not an action is considered to be a synchronization transition.
- incoming: a transition is an incoming transition if it is received
from some external source. We have no choice but to accept incoming
transitions and we cannot fire them ourselves.
- outgoing: a transition is an outgoing transition if it is the
result of another incoming transition. Incoming and outgoing declares
the two directions in which a message can go.
An interesting property of these is that the parameterizations of
a number of transition are mentioned as they are. For instance, the
lock transition is declared as:
-
- transition(lock(_,_)).
step(lock(X,Y),.....
where the two free variables X and Y can be filled in when appropriate.
This fact allows us to reason about a colored Petri-net in an abstract
way. This is a huge performance-improvement because, we can now easily
check how we can enable SetPosition(12,13) without actually
having a marking at hand. Therefore we need to check out how we can
enable SetPosition(X,Y) and try to match the resulting
relative marking, which will contain a token such as locked(_,_).
This allows for the creation of an abstract description how to enable
the SetPosition token, something which would be very difficult
with a completely expanded Petri-net.
![\begin{algorithm}
% latex2html id marker 4320
[!htp]
\begin{list}{}{
\setlengt...
...
Obtaining the possible future traces
given an initial marking.}
\end{algorithm}](img316.png)
WITH THE ABOVE PROLOG RULES in place we can relatively easy
deduce what can happen given a certain marking. Essentially to know
all possible future branches after one step, given a certain marking,
we simple state:
-
- :- step(Transition,marking,Result)
The result will give all possible answers, including the transition
executed and the result after executing the transition. If we would
like to know what possible branches exists after two steps we simply:
-
- :- step(Transition1,marking,Intermediate),
step(Transition2,Intermediate, Result)
If we continue this line of thought we can easily see how we can enumerate
all possible future traces given a certain depth and initial marking.
Algorithm 20 shows how this can be done. The
fwd_step rule will expand a marking into all possible
futures. The fwd_steps takes a list of nodes, which
can be either expanded or unknown. Unknown nodes are expanded one
step further when executing fwd_steps. Expanded nodes
are simply followed. With this we can construct a tree that can be
expanded a bit further every time.
With this rule-set we can easily track down how we can enable a certain
transition, or reach a certain marking. All we have to do is check
whether the transition we want to enable (or the marking we want to
reach) is present in one of the possible futures. If it isn't we can
go one step deeper.
A small problem remains to be explained here. When finding out how
we can go from 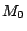 to
to 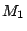 we can only investigate synchronization
actions. For example, it should not be possible for such a trace to
contain a joinActor message because the adaptor cannot
choose to send out its message since it is part of the
we can only investigate synchronization
actions. For example, it should not be possible for such a trace to
contain a joinActor message because the adaptor cannot
choose to send out its message since it is part of the 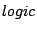 interface.
interface.
![\begin{algorithm}
% latex2html id marker 4382
[!htp]
\begin{list}{}{
\setlengt...
...mall\par
}\end{list}\par
\caption{
Printing out the trace tree.}
\end{algorithm}](img317.png)
Algorithm 21 can be used to print out such a
trace. For instance, given a certain initial marking, we can have
a result such as:
-
- start
. lock(_G410,_G411)
. . lock(_G594,_G595)
. . lock_false
. . lock_true
. . return_unlock_false
. return_unlock_false
. . lock(_G707,_G708)
. . return_unlock_false
This states very simply that, given the start situation, we can choose
to execute lock(_,_) or return_unlock_false.
It is clear that only the first one is under control of the client,
because a return_unlock_false must be issued by the
server. The possible tracks from there on are either again to lock
or to receive a lock_false, lock_true
or return_unlock_false.
![\begin{algorithm}
% latex2html id marker 4447
[!htp]
\begin{list}{}{
\setlengt...
...n{
Obtaining the possible past traces given an
initial marking.}
\end{algorithm}](img318.png)
Given a Petri-net and a marking we can also, in a similar way, deduce
which actions could have led to this marking. This is illustrated
in algorithm 22 and is similar to algorithm 20.
8.5 Reachability Analysis: Forward and Backward
Tracing
![\begin{algorithm}
% latex2html id marker 4494
[!htp]
\begin{list}{}{
\setlengt...
...there is a common marking, the way to reach
it will be printed.}
\end{algorithm}](img319.png)
![\begin{algorithm}
% latex2html id marker 4549
[!htp]
\begin{list}{}{
\setlengt...
... out \emph{how} to get from a given marking
to another marking.}
\end{algorithm}](img320.png)
TYPICALLY, SEARCH ALGORITHMS, such as implemented in the
forward or backward tracer, behave exponentially because the search
tree expands exponentially. If the search algorithm looks at depth
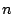 , it will take approximately
, it will take approximately 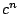 time to find a solution,
with
time to find a solution,
with 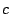 being a constant. So, if we can reduce the search depth
by halve we can find a solution
being a constant. So, if we can reduce the search depth
by halve we can find a solution 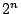 times faster. With the ability
to trace into the future and into the past we can find a solution
to the reachability problem faster. The only thing we need to do therefore
is going forward (from
times faster. With the ability
to trace into the future and into the past we can find a solution
to the reachability problem faster. The only thing we need to do therefore
is going forward (from 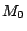 ) and backward (from
) and backward (from 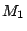 ) at the
same time. When a common marking exists between both traces, then
we have found a possible path. Algorithm 23 illustrates
how we can check if two traces matches. Algorithm 24
will determine the different strategies possible to go from
) at the
same time. When a common marking exists between both traces, then
we have found a possible path. Algorithm 23 illustrates
how we can check if two traces matches. Algorithm 24
will determine the different strategies possible to go from 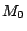 to
to 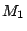 .
.
Figure 8.2:
The trace-tree to reach a marking that bring position
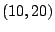 in locking.
in locking.
|
|
To illustrate the power of these rules, we will find out how we can
enable position 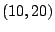 on a whiteboard, given an initial marking.
Figure 8.2 illustrates how the process works. On one
track we have a forward reasoning (the top of the figure). This process
determines that a possible future from the initial marking is lock(_,_).
A second future is the possibility that a return_unlock_false
comes back. However, this event cannot be controlled by the client
because it is an incoming event, thus we ignore this possibility.
on a whiteboard, given an initial marking.
Figure 8.2 illustrates how the process works. On one
track we have a forward reasoning (the top of the figure). This process
determines that a possible future from the initial marking is lock(_,_).
A second future is the possibility that a return_unlock_false
comes back. However, this event cannot be controlled by the client
because it is an incoming event, thus we ignore this possibility.
The second process is a backward trace (the bottom half of the drawing),
which correctly deduces that in the past a lock(10,20) could
have been present, or a return_unlock_false, return_unlock_true or
a lock_false.
The process of finding a matching trace stops here because the marking
at lock(_X,_Y) can be unified with the marking at lock(10,20).
THE PRESENTED ALGORITHM has been tested with all the conflicts
presented in chapter 6. However, because the prolog
code was not integrated within Java, we had to test the code off-line.
Therefore we obtained a start-marking from the Petri-net by exporting
one from the Petri-net evaluator. After importing it into the prolog
program, we asked the reachability program to enable a certain transition.
In all cases the result was calculated immediately (no human observable
time delay on a standard Intel processor). To a certain extent this
is normal because most interfaces provide a certain functionality
and are supposed to make state-changes easy and not difficult. An
API which requires less messages to change a state than another API
is clearly easier to use.
Now, the reachability analysis is calculated immediately, nevertheless
it took some doings before we were able to come up with such a result.
Prolog is a declarative language and is perfectly suited to find ways
to prove statements. Every solution of such a prove is a way to reach
a certain marking. Nevertheless, how the evaluator 'proves' a reachability
statement can greatly affect the performance of finding solutions.
This has forced us to insert our a) own delete operation, b) to make
a distinction between delete and append, and c) split the step predicate
into 4 parts depending on which variables are bound. We now explain
the details.
The reason why we declare our own del_marking lies in
the fact that swi_prolog (the implementation of prolog we have been
using) is only able to delete one element from a list. The predicate
delete([1,2,3],X,Y). results in only one answer:
-
- X = 1
Y = [2, 3] ;
No
while the predicate del_marking([1,2,3],X,Y). results
in all possible elements taken from the input list:
-
- X = 1
Y = [2, 3];
X = 2
Y = [1, 3];
X = 3
Y = [1, 2];
No
By relying on our del_marking predicate we are sure that
all tokens present at a certain place will be tried to satisfy the
precondition of a transition. If we used the standard delete predicate
this was not possible.
Maybe it could be possible to use select/3 as an unification
of a delete/3 and an append/3 operation. This
however would result in drastic performance penalties because there
is a subtle difference between an append/3 operation and
a select/3 operation. Select is defined as
-
- select(X, [X | L], L).
select(X, [Y | L], [Y | R]) :- select(X, L, R).
We can indeed use this predicate to implement a delete operation.
In fact del_marking(X, Y, Z) :- select(Y, X, Z). However,
if we would implement an append/3 as the inverse of a
delete, or by means of the select predicate then a simple append of
two small lists, written down as select(5, X, [6]) would
result in:
-
- X = [5, 6] ;
X = [6, 5] ;
No
This in contrast with the standard append/3 operation,
which will return only one answer: append([5],[6], X)
-
- X = [5, 6];
No
Because the lists we are using represent tokens present at certain
places the order of elements is of no importance. However, if we use
something like select/3 we would receive the same tokens
at least two times. (To be exact, we receive the same tokens 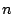 times, with
times, with 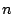 the number of elements in the target list). Because
our search algorithm is constantly adding and deleting elements from
markings, the search time would increase drastically. For every add_marking
we would create at least two new branches. On the other hand,
if we simply use the append/3 operation, we avoid the
introduction of useless branches in the search tree.
the number of elements in the target list). Because
our search algorithm is constantly adding and deleting elements from
markings, the search time would increase drastically. For every add_marking
we would create at least two new branches. On the other hand,
if we simply use the append/3 operation, we avoid the
introduction of useless branches in the search tree.
Wouldn't it be better to write a step with only one set of marking
modifications instead of a step which, depending on which variables
are bound behaves differently. The answer to this question is twofold.
First, if both the input marking and output marking are unknown then
the behavior is clearly different because we must assume that we are
working with a relative marking (a marking only describing the necessary
tokens), hence we start with empty token sets which will be filled
up by the step predicate. The other case, when one of the input or
output markings is bound requires also different behavior for every
possibility:
- if both the input and output marking are bound then we must simply
verify whether the necessary tokens are present. We can do this by
removing the elements from involved markings.
- if only the input marking is known, we must first remove
the necessary tokens from the input marking and afterward we can
put the appropriate tokens in the output marking.
- if only the output marking is known, we must first remove the
necessary tokens from the output marking and then we can deduce
which tokens should have been present in the input marking and put
them there.
As can be seen, the order in which the tokens are investigated is
important and different. This order is not strictly necessary, however,
it greatly increases the performance of one step. Finding out what
kind of tokens we could append to the unbound marking and then verifying
whether these tokens can be found in the bound marking can easily
lead to an infinite list of similar answers. Every new possible unbound
variable might always be bound to the same token later on. We consider
it better to get rid, as fast as possible, of free variables by actually
binding them to one of the available tokens and then creating the
required tokens for the unbound marking. By doing so, we a) increase
the speed of the reachability analysis and b) get rid of a possible
infinite amount of answers.
By implementing the step as we did, we do not break the declarative
programming style. The step predicate can be used in any way necessary.
For the user of step it behaves perfectly declarative.
The only thing we did by introducing a verification of the boundedness
of the variables is increasing performance.
The concurrency module its responsibility is to bring the server component
in a required state. More specifically, the required state is defined
by the incoming 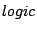 message because every incoming
message because every incoming 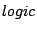 message
must be accepted by the server. To make sure that the server keeps
behaving correct, we restricted the possibilities of the enforce-action
module to only interleave new
message
must be accepted by the server. To make sure that the server keeps
behaving correct, we restricted the possibilities of the enforce-action
module to only interleave new 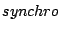 messages. However, one problem
was not anticipated, certain concurrency strategies require the ability
to bring a server and its resources back to an old state. These servers
typically embody a rollback mechanism. To allow this kind of logic,
the reachability program must be modified to allow the use of
messages. However, one problem
was not anticipated, certain concurrency strategies require the ability
to bring a server and its resources back to an old state. These servers
typically embody a rollback mechanism. To allow this kind of logic,
the reachability program must be modified to allow the use of 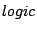 messages.
messages.
IN THIS CHAPTER we have shown how logic programs allow us
to deduce easily how we can enable certain transitions. The process
is fairly simply described in prolog but compared to standard formal
reachability techniques it is fairly advanced:
- It takes advantage of the colored Petri-net description. Instead of
expanding a colored net to all its elementary places, the process
works on a high level of abstraction by keeping variables as long
as possible variable and unifying them only in the end.
- It takes advantage of the possibility to reason in an abstract way
about a marking. It does not require a fully described marking, it
suffices to work only with the smallest necessary sub-markings. This
results in a distinct advantage over other methods because all the
possibilities introduced by non-relevant tokens are removed.
- It reduces the search space drastically by doing a forward trace as
well as a backward trace at the same time.
With this information, we can, given a petri-net description, a current
marking and a target marking, easily deduce which actions should be
taken to either a) enable a certain transition or b) place a certain
token at a certain place. This enables us to create an adaptor that
effectively bypasses the concurrency interface at a component, because
all incoming actions will always be executed, no matter what state
the component is in.
Werner
2004-03-07
![]() from
from ![]() .
.
![]() ), which we want to reach, we investigate the use of
these formal techniques. Reachability is decidable [EN94].
However it might take a long time. Generally, it can be solved in
exponential time. However for a lot of Petri-net classes different
results exist. For instance:
), which we want to reach, we investigate the use of
these formal techniques. Reachability is decidable [EN94].
However it might take a long time. Generally, it can be solved in
exponential time. However for a lot of Petri-net classes different
results exist. For instance:
![]() which brings marking
which brings marking ![]() to marking
to marking ![]() .
E.g., step(lock(X,Y),[],N) will find all possible resulting
markings N after executing the lock(X,Y) transition.
This is illustrated in algorithm 19. Depending
on whether M, N or T are known the behavior is different.
.
E.g., step(lock(X,Y),[],N) will find all possible resulting
markings N after executing the lock(X,Y) transition.
This is illustrated in algorithm 19. Depending
on whether M, N or T are known the behavior is different.
![]() to
to ![]() we can only investigate synchronization
actions. For example, it should not be possible for such a trace to
contain a joinActor message because the adaptor cannot
choose to send out its message since it is part of the
we can only investigate synchronization
actions. For example, it should not be possible for such a trace to
contain a joinActor message because the adaptor cannot
choose to send out its message since it is part of the ![]() interface.
interface.
![]() , it will take approximately
, it will take approximately ![]() time to find a solution,
with
time to find a solution,
with ![]() being a constant. So, if we can reduce the search depth
by halve we can find a solution
being a constant. So, if we can reduce the search depth
by halve we can find a solution ![]() times faster. With the ability
to trace into the future and into the past we can find a solution
to the reachability problem faster. The only thing we need to do therefore
is going forward (from
times faster. With the ability
to trace into the future and into the past we can find a solution
to the reachability problem faster. The only thing we need to do therefore
is going forward (from ![]() ) and backward (from
) and backward (from ![]() ) at the
same time. When a common marking exists between both traces, then
we have found a possible path. Algorithm 23 illustrates
how we can check if two traces matches. Algorithm 24
will determine the different strategies possible to go from
) at the
same time. When a common marking exists between both traces, then
we have found a possible path. Algorithm 23 illustrates
how we can check if two traces matches. Algorithm 24
will determine the different strategies possible to go from ![]() to
to ![]() .
.
![]() on a whiteboard, given an initial marking.
Figure 8.2 illustrates how the process works. On one
track we have a forward reasoning (the top of the figure). This process
determines that a possible future from the initial marking is lock(_,_).
A second future is the possibility that a return_unlock_false
comes back. However, this event cannot be controlled by the client
because it is an incoming event, thus we ignore this possibility.
on a whiteboard, given an initial marking.
Figure 8.2 illustrates how the process works. On one
track we have a forward reasoning (the top of the figure). This process
determines that a possible future from the initial marking is lock(_,_).
A second future is the possibility that a return_unlock_false
comes back. However, this event cannot be controlled by the client
because it is an incoming event, thus we ignore this possibility.
![]() message because every incoming
message because every incoming ![]() message
must be accepted by the server. To make sure that the server keeps
behaving correct, we restricted the possibilities of the enforce-action
module to only interleave new
message
must be accepted by the server. To make sure that the server keeps
behaving correct, we restricted the possibilities of the enforce-action
module to only interleave new ![]() messages. However, one problem
was not anticipated, certain concurrency strategies require the ability
to bring a server and its resources back to an old state. These servers
typically embody a rollback mechanism. To allow this kind of logic,
the reachability program must be modified to allow the use of
messages. However, one problem
was not anticipated, certain concurrency strategies require the ability
to bring a server and its resources back to an old state. These servers
typically embody a rollback mechanism. To allow this kind of logic,
the reachability program must be modified to allow the use of ![]() messages.
messages.