Next: 4. Learning Algorithm Up: I. Preliminaries Previous: 2. Event Based Models Contents
WHEN WE WANT TO AUTOMATICALLY GENERATE an adaptor between conflicting interfaces, the program that generates the adaptor needs some knowledge about the interfaces required and provided. This chapter introduces a formal technique to specify interfaces. Specifically we will investigate the use of Petri-nets as a formal documentation technique.
AS EXPLAINED IN PREVIOUS CHAPTER every component has a number of ports. Every port embodies a certain behavior. This can be compared with the interface offered by objects in an object oriented language. This interface, typically called an application program interface (or API for short), must be documented before someone can use the functionality offered by that interface.
Often this API is nothing more than a standard listing of method-signatures.
This is clearly insufficient for our purposes for two reasons. Firstly,
method signatures have semantics incompatible with the semantics of
our ports because we are working in an event based model in which
'messages' are transmitted between components. This implies that messages
are passed by value and that a message not necessarily specifies that
a certain method needs to be called. A message can be for instance
something like ![]() . Lastly, messages, in comparison to standard
method calls, will never return a value. Therefore a simple list of
method signatures is not very well suited to document ports. A second
reason why common used API's are not suitable is that method signatures
do not specify enough information to allow a program to extract interesting
properties. This, we will show, is necessary in order to generate
an intelligent adaptor. Therefore we will now investigate which technique
is usable to formally document an interface.
. Lastly, messages, in comparison to standard
method calls, will never return a value. Therefore a simple list of
method signatures is not very well suited to document ports. A second
reason why common used API's are not suitable is that method signatures
do not specify enough information to allow a program to extract interesting
properties. This, we will show, is necessary in order to generate
an intelligent adaptor. Therefore we will now investigate which technique
is usable to formally document an interface.
COMMONLY USED FORMAL SYNTACTICAL INTERFACE DESCRIPTIONS simply state what methods can be called, with which parameters. Sometimes a type system specifies what kind of objects need to be passed. Specifying interfaces this way suits compiler and linker, and together with an informal explanation of what the interface is supposed to do, can be understood by humans. For machines, on the other hand, there is a lot of information missing within such a simple syntactical description.
Now, let us think about machines that need to understand interfaces. It is obvious that they cannot make much more sense out of simple API's than they already do (that is type checking and linking). If we want to create an adaptor, then a machine needs to understand enough of the possibilities offered by an interface. Therefore we will do what is typical done is such situations: specify this extra information in a formal way.
The problem that arises now is that, contrary to a syntactical description it is difficult to capture the semantics of an interface. How far should we describe the interaction ? Should we only describe when a certain function can be called or do we also need to specify what the arguments should look like ? If we would specify what the arguments look like do we need to specify the maximum and/or minimum size of the data transferred ? In short, it is very difficult to describe an interface in a formal way without capturing too much detail, or without giving a trivial description (such as: this function will be called at some time). The programmer should have the freedom to specify what he wants in an easy formal way. The formalism should not stop him from expressing certain requirements, it should be flexible and easy to understand. Therefore, the formalism we will use are Petri-nets.
THE FORMALISM WE WILL USE TO SPECIFY THE BEHAVIOR of an interface will be colored Petri-nets. Petri-nets were originally invented by Petri[Pet62]. Petri-nets have a number of very appealing properties. For an in-depth discussion of all these properties see [KCJ98].
It is very difficult to find a formal documentation technique that is a) as general and formal as Petri-nets and b) as useful as Petri-nets at the same time. Below we will shortly touch upon a number of techniques to do so.
Finite automatons (FSM's) and state diagrams [Har87,JMW+91,G.01] have problems when multiple concurrent sessions should be expressed and their size explodes very quickly with every newly added behavior.
Reuse Contracts [LSMD96], invented at the Programming Technology lab of the VUB, are a means to describe the behavior of an interface in an abstract way. This abstract interface description is called a reuse contract. From reuse contracts a number of properties of an implementation can be deduced, for instance reuse contracts can help in evolving a software system such that existing software dependent on the framework still functions as expected. The approach described in [LSMD96] has some drawbacks, which also form the reason why we didn't use them in our work:
Message sequence charts (MSC's) [JCJO92,Wyd01], as a documentation technique, offers example traces of what a component can do. However, message sequence charts typically documents only one run through a component and are difficult to extend to include all possible traces of a component. A second drawback of the work presented in [Wyd01] is that it is only possible to reason about the sequence of things to happen, not about the actual content of the data transmitted. For concurrent systems this is a large drawback. It is almost completely impossible to describe the semantics of a rollback-able transaction without taking the state of the resources into account.
The use of purely logical approaches that specify what conditions should be met would be possible: it is not too difficult to use predicate-logic or proposition-logic to describe the behavior of an interface to a chosen level of detail. Often this is done by using pre- and post-conditions to describe when a message can be send or received. However, since these approaches are barely readable and do not offer extra advantages over Petri-nets we chose not to use them to describe the behavior of component interfaces.
The use of temporal logics [KV97,Pnu77]
to describe when which transition is enabled could also have been
possible. Again the drawback here is the readability and the difficulties
one can have to write down even simple statements such as: 'between
every occurrence of ![]() and
and ![]() there can only be one enable or
disable transition'.
there can only be one enable or
disable transition'.
Another, well known specification technique such as SDL [OFM97,JDA97], which is widely used to specify communication protocols, can be easily mapped onto Petri-nets [FG98].
The lack of a formal semantical description of interfaces in protocols has been recognized for a long time. See [Bra01]. In the past, attempts have been made to extend CORBA IDL's with extra formal specifications in such a way that they could help in automatic checking of the protocols involved [CFP+01]. However, since we are not working with IDL's anyway there was no use in using these approaches. [BOP] discusses how Petri-nets can be used to describe the behavior of CORBA objects.
A lot of tools support Petri-net in all kinds of contexts. The main reason why we didn't use them is because we are using Petri-nets in a context in which they are generated automatically. This includes a random element and by generating pseudo-random Petri-nets we would test every tool to its limits. It is not to be expected that a tool which survives all possible Petri-nets will be found quickly. Neither would it be possible to fix bugs in such a tool because most often the source is not free. A second reason why existing Petri-net tools have not been used is that most of the existing tools are to be paid for.
However, there is one tool we did investigate because it looked very
promising: Pep. Pep [Gra] is a programming environment,
developed at the university of Oldenburg by the parallel systems group
and is based on Petri-nets in which the programmer can design the
requirements of a parallel system using a process algebra notation,
called ![]() [BH93], SDL[OFM97],
high level Petri-nets, called M-nets, or low level petri-nets. Along
with the tool comes a set of compilers which generate Petri-nets from
the different kinds of input formats. A lot of papers have been published
how certain of these languages can be mapped onto Petri-nets [BFF+95b,FG98].
The Petri-nets can be visually simulated, and the possibility exists
to link it with a 3D VRML environment. Automatic verification is also
included in Pep, by means of an integration of other packages such
as an Integrated Net Analyzer, a symbolic verification system (developed
at CMU) and others.
[BH93], SDL[OFM97],
high level Petri-nets, called M-nets, or low level petri-nets. Along
with the tool comes a set of compilers which generate Petri-nets from
the different kinds of input formats. A lot of papers have been published
how certain of these languages can be mapped onto Petri-nets [BFF+95b,FG98].
The Petri-nets can be visually simulated, and the possibility exists
to link it with a 3D VRML environment. Automatic verification is also
included in Pep, by means of an integration of other packages such
as an Integrated Net Analyzer, a symbolic verification system (developed
at CMU) and others.
Pep's big attraction is due to the good programming documentation and documented internals. The whole abstract Petri-net notation is given in an understandable form. Its drawbacks on the other hand are its incorrect conversion from high level petri-nets to low level petri-nets and its wrong execution of high level petri-nets. It seems as if every high-level place acts as a queue on which messages can come in and whenever a transition needs to be checked only the top level elements are checked. In most cases this is suitable and this is certainly suitable if the Petri-nets are generated automatically. However, a suitable combination of tokens, such as is required from colored petri-nets, is not the case, which makes executing an automatically generated Petri-net an impossible case. Another drawback of Pep is that its Petri-net file format is very rigorous and unreadable. Specifying a Petri-net is difficult because there are cross-linked labels and references almost everywhere. This is something which is a) unnecessary and b) difficult to keep track of when specifying a Petri-net.
A second tool we wanted to investigate, is CPNet. This is the tool promoted by the author of [Jen94], is sold to companies and is supposed to be free for universities. However after contacting the authors 3 times we still didn't get any answer.
PETRI-NETS ARE OFTEN DRAWN AS BOX/CIRCLE DIAGRAMS. Figure 3.1 is a box/circle diagram of a Petri-net describing the behavior of a non-counting semaphore. Petri-nets have a number of concepts:
![\includegraphics[%
width=1.0\textwidth]{CPN-NestedLocking.eps}](img41.png)
|
Given this, we can now clearly see the expressive power of Petri-nets. We can choose how much detail we include in our Petri-net. The Petri-net given in figure 3.2 only covers the locking of a single square with a lockcount. If we want we could add a session ID to check whether the incoming lock request is from the same one who already has obtained a lock. The fact that we do not need to specify this, without losing the ability to reflect over the behavior of the system is one of the greatest strengths of Petri-nets.
It is even possible to describe the same behavior with only one place.
Therefore we need to add another color ![]() which describes whether
a certain position is in busy locking (busyL), busy unlocking (busyU)
or available (avail). The associated Petri-net, without acting logic
for the sake of simplicity is pictured in 3.3.
On the other hand if we need to use this Petri-net in a larger context,
in which we only need to know whether a place is locked or unlocked
we can split the LockCount state of figure 3.2
in two as depicted in figure 3.4.
which describes whether
a certain position is in busy locking (busyL), busy unlocking (busyU)
or available (avail). The associated Petri-net, without acting logic
for the sake of simplicity is pictured in 3.3.
On the other hand if we need to use this Petri-net in a larger context,
in which we only need to know whether a place is locked or unlocked
we can split the LockCount state of figure 3.2
in two as depicted in figure 3.4.
![\includegraphics[%
width=1.0\textwidth]{CPN-NestedLockingLarge.eps}](img60.png)
|
Simple Petri-nets, which we will need later on, are Petri-nets in which tokens cannot contain a color. They only can be at a certain place. A simple Petri-net only allows for one token per place. A simple Petri-net also doesn't have guard, input or output expressions.
We will now define Colored Petri-nets formally. The definition given
below is based, to a large extent, on the well known work of [Jen94].
Mainly we have removed some
![]() and
and
![]() mappings, however this does not modify the formalism it merely simplifies
it for our purposes. The often-used and referenced definition given
in [Jen94] is not the first definition given of colored
Petri-nets, other definitions also exists such as referenced in [EK98,Lak94].
However, they are not explained in as much detail as the one we will
use.
mappings, however this does not modify the formalism it merely simplifies
it for our purposes. The often-used and referenced definition given
in [Jen94] is not the first definition given of colored
Petri-nets, other definitions also exists such as referenced in [EK98,Lak94].
However, they are not explained in as much detail as the one we will
use.
Before we can explain the details of colored Petri-nets we need the ability to describe multiple tokens at the same place. Since this is something that cannot easily be expressed with mathematical sets, we resort to multi-sets.
A multi-set is a set in which every element can occur multiple
times. Formally a multi-set ![]() is defined over a certain underlying
set
is defined over a certain underlying
set ![]() as a function that maps every element of S to a natural number:
as a function that maps every element of S to a natural number:
![]() . The domain of the multi-set: the occurency
counts of every possible element of
. The domain of the multi-set: the occurency
counts of every possible element of ![]() are called the coefficients
of
are called the coefficients
of ![]() . All possible multi-sets associated with a certain set
. All possible multi-sets associated with a certain set ![]() will be denoted as
will be denoted as ![]() . This should not be confused
with the power-set, denoted
. This should not be confused
with the power-set, denoted ![]() which is the set of all possible
subsets.
which is the set of all possible
subsets.
A second preliminary before we can explain the formal side of colored
Petri-nets concerns expressions. The guards and actions work
on values. The way in which these are represented is currently left
open, any type of expression can be inserted into a colored Petri-net.
For example, one can use ![]() expressions, or simple algebraic
expressions. One can choose whatever fits best. If one chooses a language
too expressive a certain level of formal analysis will no longer be
possible. We will discuss this later on. Once one has chosen an expression
language one cannot change this anymore within the same Petri-net.
In the following definitions we will refer to an expression as
expressions, or simple algebraic
expressions. One can choose whatever fits best. If one chooses a language
too expressive a certain level of formal analysis will no longer be
possible. We will discuss this later on. Once one has chosen an expression
language one cannot change this anymore within the same Petri-net.
In the following definitions we will refer to an expression as ![]() .
.
![]() (with a capital) refers to all possible expressions. For every
expression
(with a capital) refers to all possible expressions. For every
expression ![]() it should be possible to obtain the type
and free variables. We should also be able to evaluate it under a
certain binding of values to variables:
it should be possible to obtain the type
and free variables. We should also be able to evaluate it under a
certain binding of values to variables:
|
The above describes the static structure of a CPNet. Figure 3.1 describes in a formal way the the Petri-net pictured in figure 3.3.
To describe the dynamic behavior of a CPNet we will first describe what a marking is, then describe when a transition is enabled and finally what happens when a transition is executed. But before we do so, some syntactic sugar is introduced.
The set of all bindings for ![]() is called
is called ![]() . A token element
is a couple
. A token element
is a couple ![]() with
with ![]() and
and ![]() . A binding elements
is a couple
. A binding elements
is a couple ![]() with
with ![]() and
and ![]() . The set of all
possible token elements is called
. The set of all
possible token elements is called ![]() , the set of all possible binding
elements is called BE. Now we can define a marking:
, the set of all possible binding
elements is called BE. Now we can define a marking:
A marking is a multi-set over ![]() . The initial marking
. The initial marking ![]() is obtained from
is obtained from ![]() as follows
as follows
A transition ![]() is enabled if a) there exist a binding satisfying
the guard (
is enabled if a) there exist a binding satisfying
the guard (![]() ) and b) all expressions placed on the incoming
arcs result in something of the correct type. We will denote this
as
) and b) all expressions placed on the incoming
arcs result in something of the correct type. We will denote this
as ![]() , which specifies that transition
, which specifies that transition ![]() is enabled
under marking
is enabled
under marking ![]() . Formally,
. Formally,
![]() will be called the postcondition of
will be called the postcondition of ![]() . When an enabled
transition
. When an enabled
transition ![]() is executed (fired) the marking
is executed (fired) the marking ![]() changes to
changes to
![]() as follows :
as follows :
A shorthand notation
![]() will be used to denote
the set of all possible future markings after firing one of the enabled
transitions.
will be used to denote
the set of all possible future markings after firing one of the enabled
transitions.
For both shorthand notation, ![]() and
and
![]() ,
which both specify what can happen next, two other notations exist,
which describe what could have happened before.
,
which both specify what can happen next, two other notations exist,
which describe what could have happened before. ![]() is
called the pre-condition of
is
called the pre-condition of ![]() .
.
The above formal definition of Colored Petri-nets can be scaled down to Elementary Place Transition nets. To do so, the concept of multiple tokens per place, different colors per token and (input-, output- and guard-)expressions has to be removed. The resulting net has almost the same dynamics as a colored Petri-net, however, because only one token is allowed per place, a transition is only enabled when none of its output places contains a token.
Below we explain that implementing an efficient evaluator for Colored Petri-nets is in general difficult. Later on this might pose some problems when testing verifying certain requirements.
Petri-nets can be implemented on control-flow machines, that is, machines with a 'fetch', 'execute', 'store', architecture. To do so one needs to keep a marking in working memory. With every time-step this marking is used to verify which transitions are enabled. The current marking in the working memory is then replaced by the new marking.3.1 However fast in execution, a typical control flow machine suffers from one bottleneck: the memory access: since every single Petri-net step has to fetch and store data in the main working memory, Petri-nets are difficult to map efficiently to commonly used hardware.
Nevertheless, in the past, data-flow machines have been built which are much more efficient in executing Petri-nets. A data-flow machine consists of a number of registers that hold tokens; a token is transferred from operation to operation. In a typical data-flow machine an operation has at most two input-registers and at most two output operations. The input registers are filled in by other instructions that want to pass a token to this operation. The destination registers contain the addresses where to put the result in. These addresses refer to the input registers of other operations. Every operation has also two signaling registers which are used to schedule the passing of tokens. [Moo96] contains a description of a number of existing data-flow machines. Not so strangely the evolution of data-flow machines follows very closely the evolution of formal Petri-net models.
Implementing an evaluator for colored Petri-nets seems trivial: instead
of checking whether a token is present and moving the token from the
input places to the output places we also have to check a guard. Unfortunately
it isn't that simple. Remember the formula 3.2,
if we want to know which transitions are enabled we must be able to
evaluate the right hand side of that expression. This means that we
must find a binding for which the guard (and accompanying expressions)
is satisfied. In contrast to an elementary net where we simply have
to check whether a token is present we now have to find out which
combination of tokens is suitable to satisfy the guard. Fortunately,
when searching a suitable combination we only need to take into account
the set of all tokens present in places local to the transition under
investigation. This means that we don't have to check combinations
of tokens in places which are not immediately linked to the current
transition. This can be easily seen if we look at the two expressions
within formula 3.2. The first requirement,
(there should be a ![]() ), does not necessarily guarantee that
the values are present in the places local to
), does not necessarily guarantee that
the values are present in the places local to ![]() . In fact nothing
indicates where the values have to come from. It only guarantees that
there is a binding which satisfies the guard and which binds all necessary
values. The second part of the expression on the other hand
. In fact nothing
indicates where the values have to come from. It only guarantees that
there is a binding which satisfies the guard and which binds all necessary
values. The second part of the expression on the other hand
![]() guarantees that all the values necessary to satisfy the guard are
present at the incoming places.
guarantees that all the values necessary to satisfy the guard are
present at the incoming places.
In practice this means that, when a transition has ![]() tokens in
total over all its input places (this set is called
tokens in
total over all its input places (this set is called ![]() and there
are
and there
are ![]() free variables (this set is called
free variables (this set is called ![]() we must try out
all combinations over X. If there are many tokens this number grows
exponentially. Hence we cannot check whether a transition is enabled
in
we must try out
all combinations over X. If there are many tokens this number grows
exponentially. Hence we cannot check whether a transition is enabled
in ![]() (as can be done with Elementary Nets). A second aspect
in evaluating a Petri-net is knowing which transitions have a chance
to be enabled. If we start with an initial marking
(as can be done with Elementary Nets). A second aspect
in evaluating a Petri-net is knowing which transitions have a chance
to be enabled. If we start with an initial marking ![]() we know
that we only have to check the transitions immediately bound to the
places containing tokens. So we only need to check out
we know
that we only have to check the transitions immediately bound to the
places containing tokens. So we only need to check out
![]() .
If a certain transition is selected to be executed we need to change
the marking from
.
If a certain transition is selected to be executed we need to change
the marking from ![]() to
to ![]() as specified in formula 3.3.
In human terms this equation transfers a certain number of tokens
from the input place(s) to the output place(s), thereby changing the
local states of all the input places and all the output places, formally
changing the state of
as specified in formula 3.3.
In human terms this equation transfers a certain number of tokens
from the input place(s) to the output place(s), thereby changing the
local states of all the input places and all the output places, formally
changing the state of
![]() . The transitions
connected to these places:
. The transitions
connected to these places:
![]() are the only ones who can possible change from disabled to enabled
(or vice versa).
are the only ones who can possible change from disabled to enabled
(or vice versa).
Because of this, it is important to have Petri-nets with enough distinct places: the number of incoming tokens in a transition will likely be smaller if we have more places in a Petri-net. For example, a Petri-net as in figure 3.3 is very small, with only one place. Given the fact that the net is conservative3.2 and that we start with 3072 tokens, and there are 5 possible enabled transitions, we need to check out 15360 possibilities. This number rises exponentially with the number of input tokens taken by one transition. In comparison, consider the Petri-net in figure 3.2, we start with a token count of 1024 at place LockCount. There are 3 possible output places so we need to check 3072 combinations.
Given the fact that we need to try out all combinations of incoming tokens we might start thinking of using something like a logic engine to evaluate a Petri-net. Indeed, it is very easy to write a Petri-net evaluator in prolog [Fla94]. To do so one simply needs to translate the formal definition of a Petri-net to prolog rules as we will do in chapter 8.
THE FORMAL DEFINITION of a colored Petri-net given earlier handled expressions in an abstract way. Therefore we need to define what kind of expressions we will use. The syntax:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Semantically speaking those expressions are straight forward. In the end everything evaluates to either a token or an integer. There are no other values to work with. If a compound statement is found, the arguments are evaluated in applicative order: they are all evaluated recursively, after that the operator is applied to the given values.
We now define the ![]() operator on expressions.
operator on expressions.
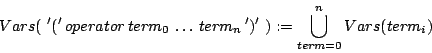
![\begin{displaymath}
Vars( '[' term_{0} \ldots term_{n} ']' ):=\bigcup_{term=0}^{n}Vars(term_{i})\end{displaymath}](img180.png)
The ![]() operator on expressions is defined as
operator on expressions is defined as
with ![]() either
either
![]() and arithmetic one
of
and arithmetic one
of ![]() . Because all operators work on integers the values assigned
to variables can only be integers.
. Because all operators work on integers the values assigned
to variables can only be integers.
WE ARE ABOUT TO USE COLORED PETRI-NETS to describe the behavior of a component. Since a) programmers are supposed to write these and b) our adaptor generation software needs the ability to read and understand them we need a text format to write Petri-nets down in a clear and understandable way, hence:
Therefore, we came up with the following basic Petri-net syntax. We also implemented a prototype of a Petri-net evaluator based on this syntax in Java. The Petri-nets are based on the expression syntax given earlier.
![]()
![]() (place
(place ![]()
![]() )
)
![]() (transition
(transition ![]()
![]()
![]()
![]() )
)
![]() (input
(input
![]() )
)
![]() (output
(output
![]() )
)
![]() (guard
(guard
![]() )
)
With this notation it is easy to write down Petri-net of figure 3.2.
(place Locking)
(place UnLocking)
(place Acting)
(transition Lock
(input LockCount[X,Y,C])
(output Locking [X,Y,C]))
(transition Lock_True
(input Locking[X,Y,C])
(output LockCount[X,Y,C+1]))
(transition Lock_False
(input Lock_False[X,Y,C])
(output LockCount[X,Y,C]))
(transition UnLock
(input LockCount[X,Y,C])
(output UnLocking[X,Y,C])
(guard (> C 0)))
(transition UnLock_Done
(input UnLocking[X,Y,C])
(output LockCount[X,Y,C-1]))
Before we can actually use Petri-nets in an execution environment our Petri-nets need to be linked to this environment. Commonly, Petri-nets have a provision for this under the form of sources and sinks. A source is a place where 'out of the blue' tokens can arrive without prior notification. A sink is a place where the Petri-net can place a token and this token will be automatically removed to perform some action.
Informally a source-place is a place for which there are no incoming arcs. A sink place is a place for which there are no outgoing arcs. Formally this can be written down as
Similarly,
However, sources and sinks are not only defined based on their presence in the Petri-net. They also have an external behavior associated with them, which is often not expressed within the Petri-net. Below we will define a suitable behavior for sources and sinks such that it can be used within an event based framework.
The component framework outlined earlier (chapter 2) describes how ports and components can be used to write adaptors easily. The main idea behind the framework is that messages should be the only way to communicate events between components. Therefore it is a logical extension to link every message to a token. Converting messages to tokens and vice versa is done by a set of conversion rules. Every rule describes what a message looks like and declares how the token should be created. Syntactically we define this,
![]() (message
(message
![]()
![]() )
)
![]() (field
(field
![]()
![]() )
)
Converting a message to a token, given a set of such message rules, is done by retrieving all of the unbound variables, sorting them alphabetically and placing them inside a token. For instance
(field ``X'' X)
(field ``Y'' Y)
(field ``Result'' 1))
![\includegraphics[%
height=8cm]{SourceSinkDemo.eps}](img210.png)
|
These message rules give us a means to convert messages to and from tokens. This is necessary to be able to interface a Petri-net with our external component framework. The only thing we still need to define is the way sources and sinks are written down. A source place is a place which generates tokens. In our case, tokens are generated when messages arrive, therefore a source place is described by means of a string (the name), an integer which specified over which port the messages comes from and a message template. Sink places are specified in a similar way.
![]() (source
(source ![]()
![]()
![]() )
)
![]() (sink
(sink ![]()
![]()
![]() )
)
The extra
![]() field is necessary for sources
to specify the port over which the message comes. For sinks it is
necessary to specify the port to which the message should go to. Figure
3.5 illustrates how sources (left side, ending on
-in) and sinks (right side, ending on -out) can be used to specify
a required message interaction between components.
field is necessary for sources
to specify the port over which the message comes. For sinks it is
necessary to specify the port to which the message should go to. Figure
3.5 illustrates how sources (left side, ending on
-in) and sinks (right side, ending on -out) can be used to specify
a required message interaction between components.
Because this kind of Petri-nets (with sources and sinks) quickly becomes very large, it is impractical to request from the developer to write down all sources and sinks and link them together. However, there are two more reasons why a developer should not write the sources and sinks explicitly down.
One of the ideas behind the component framework is that one needs the ability to specify the inverse of an interface. To illustrate this think of a server that offers a locking strategy and a client that expects a locking strategy. The server will specify an incoming Lock message and outgoing LockTrue and LockFalse messages. The client on the other hand will specify exactly the contrary: Lock messages go out and LockTrue or LockFalse messages come in. This can be seen in figure 3.6 and 3.7. The red interface boxes (left) are the ones going toward the server, the blue interface boxes (right) are the ones coming from the client. In practice, the colored transitions are replaced by sources and sinks to match certain messages. The translation from such an incoming or outgoing transition to source and sink places is however not always the same because multiple reasons exist to create such an adaptor.
The first situation is one in which an adaptor traces the behavior of an interaction, without adapting anything. This is useful to test the correct working of both components and the Petri-net specification of the interface. Using such an adaptor ensures that the formal description is in tune with the implementation of the component.
A second situation occurs when an adaptor is required to adapt the behavior of two interfaces. In such a situation there will be two Petri-nets available: one accepting messages from the client and one accepting messages from the server. Both Petri-nets and some 'adaption' logic will reside in the adaptor.
These two cases offer some problems because the behavior of the Petri-net transitions is different. To understand this look at the required behavior of the red and blue lines connected to the transitions. Depending on the situation a transition should behave different
The extended Petri-net notation:
![]() (intransition
(intransition ![]()
![]()
![]()
![]()
![]() )
)
![]() (outtransition
(outtransition ![]()
![]()
![]()
![]()
![]() )
)
In order to be able to transform the in-transitions and out-transitions to an executable Petri-net we have added special source and sink places (as is done in almost all Petri-net tools). In figures 3.8 and 3.9, the source places are colored green and will contain a token when a message arrives, the sink places are colored red and the underlying component will sent out a message when a token arrives at those places.
![\includegraphics[%
width=0.70\textwidth]{InOutTransitionConvertionTracer.eps}](img216.png)
|
Transforming a Petri-net to be used in a tracing Petri-net adaptor (illustrated in figure 3.8):
![\includegraphics[%
width=0.70\textwidth]{InOutTransitionConvertionAdaptor.eps}](img221.png)
|
Transforming a Petri-net to be used in an adaptor (illustrated in figure 3.9), requires another transformation logic for the in/out transitions; For the left port this becomes
IN THIS SECTION WE GIVE TWO examples of more difficult locking interfaces that can be expressed by means of Petri-nets. The first example covers a layered concurrency strategy. The second covers a rollback-able concurrency strategy.
![\begin{algorithm}
% latex2html id marker 1622
[!htp]
{}
\begin{list}{}{
\setle...
...tri-net description of a blocking layered concurrency strategy.}
\end{algorithm}](img223.png)
Figure 3.10 contains an example of a layered concurrency strategy that works in different stages. This example demonstrates how well suited Petri-nets can be to describe subtle interaction patterns between different 'modes' of an interface. The concurrency interface itself describes a) the behavior that can be executed upon certain resources and b) the synchronization behavior that need to be used before these resources are accessible. The concurrency strategy is layered. This means that, before the actual resources can be locked, the server needs to be locked entirely by the client. Once all the locks are obtained the server itself can be released, such that other component might start a set of locking operations. This example has a number of interesting features
![\begin{algorithm}
% latex2html id marker 2057
[!htp]
{}
\begin{list}{}{
\setle...
...net describing non-blocking rollback-able concurrency strategy.}
\end{algorithm}](img225.png)
The example given in figure 3.11 shows how a concurrency strategy that makes use of rollbacks can be written down. Locks can be requested, when they are granted they can be either committed or aborted. If a lock is aborted the previous state will be recalled, if a lock is committed the previous state is forgotten. Important features of this Petri-net are:
PETRI-NETS ALLOW THE PROGRAMMER of a component to document the required and provided interfaces of a component. Nevertheless there are some issues which should be taken into account. Not every Petri-net expresses as much as another Petri-net. For instance, one Petri-net of a component might specify that every incoming message can be handled at any time, while another Petri-net will carefully offer pre-conditions and postconditions for this message to be handled. To help the programmer write down Petri-nets that make sense we introduce some guide rules to write them:
By means of Petri-nets we will be able to define clearly what a conflict is. Therefore we will rely on the existence of a certain link between two Petri-nets. This link will consist of the common transitions and will be called the functional link. All the other transitions within a Petri-net will be considered to be part of the synchronization interface.
We will also assume that both Petri-nets are linked in such a way that the firing of one transition is mapped onto the firing of a similar transition in the other Petri-net (this can be accomplished by inserting an adaptor or by hardwiring the transitions by means of inserting common places, as we've done in section 3.6.3). For instance, when a SetPosition message arrives, then the first Petri-net will fire a SetPosition. Afterward, the second Petri-net (of the outgoing link) also needs to fire a SetPosition, otherwise no communication will occur between both components.
If the Petri-nets are used as such, then we can define a conflict
as a situation in which an incoming functional message ![]() can be
accepted by the first Petri-net, but not by the second Petri-net because
the required preconditions does not hold. E.g, an incoming setPosition
that cannot be execute on the server because the position is not locked
yet (this will be described within the server side Petri-net and will
form the blocking pre-condition of the SetPosition transition).
can be
accepted by the first Petri-net, but not by the second Petri-net because
the required preconditions does not hold. E.g, an incoming setPosition
that cannot be execute on the server because the position is not locked
yet (this will be described within the server side Petri-net and will
form the blocking pre-condition of the SetPosition transition).
Formally, two Petri-nets ![]() and
and ![]() are, given two markings
are, given two markings
![]() and
and ![]() , in conflict when a logic transition exists
that is enabled in only one of both interfaces. We will use
, in conflict when a logic transition exists
that is enabled in only one of both interfaces. We will use ![]() to denote a conflict between two Petri-net markings:
to denote a conflict between two Petri-net markings:
| (3.4) |
BELOW WE WILL INTRODUCE a number of formal properties of Petri-nets. Not all of them are decidable.
This property is decidable and forms the basis for many other properties. In chapter 8 we will explain in more detail how this kind of information can be obtained.
IN ORDER FOR AN ADAPTOR to mediate the behavior of two conflicting interfaces, it needs extra formal documentation. The formalism we will use to represent the behavior of an interface are Petri-nets because it allows us to
We wrapped up this chapter with giving some guidelines to the developer to write Petri-nets and gave a short introduction to which properties are decidable for Petri-nets.
The Petri-nets we have described here will be used further on for two purposes: