Next: II. The Case: Conflicting Up: I. Preliminaries Previous: 3. Describing Interfaces by Contents
THE FINAL CHAPTER OF THE PRELIMINARIES gives an overview of learning algorithms and how they can be used to mediate the semantic differences between different concurrency strategies. Given the context of open distributed systems, this problem cannot be solved automatically. This is because we cannot expect to have an adaptor available for every possible pair of conflicting interfaces, so we need some automatic approach.
We have a problem in which we need to create an adaptor that is able to establish meaningful communication between two components with a conflicting interface. As already mentioned in the introduction, the adaptor will be divided in three modules. One module, the liveness module, will be responsible for keeping the underlying component alive, a second module, the concurrency module, will be responsible for implementing a suitable concurrency strategy and a third module, the enforce-action module, is responsible for bypassing an existing concurrency strategy. The second and third modules can be implemented in a formal way, the first module however is computationally too complex to be able to handle formally (see liveness of Petri-nets in section 7.3.1). Therefore we will resort to a learning algorithm.
Before we can look for solutions to the problem presented we need to investigate which techniques we can use to keep the underlying component alive. We need to know what we can expect from a given learning algorithm and what kind of information it expects. In this chapter we first explain a number of important concerns with respect to learning algorithms in general, after which we will briefly introduce a number of different learning algorithms available. Secondly, based on this information we will explore the possibilities we have to map our problem on existing learning algorithms. Thirdly, we explain how genetic algorithms and genetic programs are conceived, and how we will use them in this dissertation. Fourthly, we present reinforcement learning algorithms.
A LEARNING ALGORITHM IS CHARACTERIZED by the sort of problems presented, the sort of solutions to be found and the environment in which the algorithm is supposed to work. For instance, in our case we have a problem of conflicting interfaces: the solutions we are looking for are adaptors between the conflicting interfaces and the environment includes all the limitations we place upon the adaptors. Examples of such limitations are 'an adaptor is a process', or 'an adaptor can only handle one message at a time' to 'the conflicts we are dealing with are concurrency problems'. All these implicit or explicit degrees of freedom define the search space of the learning algorithm.
Sadly there is no universal learning algorithm that will work optimally in every possible situation. Therefore learning algorithms are designed to work within certain environments. Learning algorithms cannot learn what they cannot see, and they don't work very well if they see too much information. (This is the typical bias versus variance problem). This is a bit of a disappointment for people introduced to learning algorithms because they assume that an intelligent algorithm should be able to look for other clues than the ones found in their environment. Learning algorithms will not exhibit such behavior[Mor96]. Nevertheless they can be helpful in certain domains such as character recognition, robot motion planning, robot activator control, regulation systems and others.
The number of available learning algorithms is large, and the number of variations on every algorithm itself is even larger. We can consider different criteria for classifying learning algorithms. We will discuss them below:
TO CHOSE A SUITABLE LEARNING ALGORITHM for our problem, we need to define the boundaries clearly.
BELOW WE EXPLAIN THE DETAILS OF A GENETIC ALGORITHM. We will also explain how we use them as representational testers in this dissertation.
A genetic algorithm [Gol89] is an algorithm that tries to solve a problem by trying out a number of possible solutions, called individuals. Every individual is an encoding of a number of modifiable parameters, called genes, and is assigned a fitness that measures how well the individual solves the problem at hand. From the pool of individuals a new generation of individuals is created. This can be either by preserving, mutating or crossing over individuals. This process is repeated until a suitable individual is found. An illustrative flowchart of this process is pictured in figure 4.1.
The standard questions before implementing any genetic algorithm are: What are the individuals and their genes? How do we represent the individuals? How do we define and measure the fitness of an individual? How do we initially create individuals? How do we mutate them and how do we create a cross-over of two individuals? How do we compute a new generation from an existing one? At the moment a genetic algorithm is implemented in a way that the individuals are themselves programs, we call it a genetic programming algorithm. In our implementation, the individuals could be protocol adaptors between communicating processes.
Genetic algorithms as an evolutionary algorithm to solve the problem of conflicting concurrency strategies is relatively useless in a running system, because a genetic algorithm works in general off-line and can never guarantee that the resulting adaptor will work in every possible situation. Indeed: it is very difficult to verify certain concurrency requirements such as deadlock-freedom or no race conditions. However, we will use genetic algorithms is such a way that we turn an argument against them to our advantage. This argument is the representational problem: how well does a genetic algorithm perform given a certain representation of the problem [SB92,Sch87]. Or, stated otherwise how can we create a representation that will offer a good fitness landscape.
To illustrate this, think of a problem in which an ant has to learn how to walk a line from left to right. If we use a representation of our individuals in which we only offer the generation process 'go left' and 'go right' primitives, the genetic algorithm will very easily find a solution to the problem. However if we use another representation of the individuals with operators such as 'current angle', 'current position', 'turn left x degrees', 'turn right x degrees', 'forward' and 'backward' it will be substantially more difficult to find a solution to the same problem. We will use this property of genetic algorithms (which is, in general, a big disadvantage), to determine the best representation of a solution within a given environment and fitness function. Specifically, we will keep the same environment and fitness function and will measure how fast a solution is found given a certain representation of the individuals. We consider that if a certain problem can be solved easily under a certain representation, it is a good representation. If the same genetic algorithm has more trouble finding a solution the representation might not be so suitable. In chapter 9 and chapter 11 we will use this technique to validate different representations.
However, which kind of representation are available for our problem still needs to be discussed. In general two approaches are used. First, we can use hierarchically structured, human readable/programmable programming languages such as Scheme, Lisp, Java and others to represent the behavior of the concurrency adaptor. Unfortunately, the inevitable syntactic structure imposed by these languages complicates the random generation of programs. Second, we can use a representation that is more suitable for random generation, but is in general not readable. These approaches are mainly based on classifier systems, for which we will explain the basics below.
We will now introduce one of the representations we have tested because we need them in chapter 11. This representation are classifier systems. Classifier systems [Gol89] in cooperation with genetic algorithms form a genetic programming4.1 approach that is symbolic and easy to implement. Moreover, given our problem, their symbolic nature can be to our advantage.
A classifier system is a kind of control system that has an input interface, a finite message list, a classifier list and an output interface. The input and output interfaces put and get messages to and from the classifier list. The classifier list takes a message list as input and produces a new message list as output. Every message in the message list is a fixed-length binary string that is matched against a set of classifier rules. A classifier rule contains a number of (possibly negated) conditions and an action. These conditions and actions form the genes of each individual in our genetic algorithm. Conditions and actions are both ternary strings (of 0, 1 and #). `#' is a pass-through character that, in a condition, means `either 0 or 1 matches'. If found in an action, we simply replace it with the character from the original message. Table 4.1 shows a very simple example. When evaluating a classifier system, all rules are checked (possibly in parallel) with all available input messages. The result of every classifier evaluation is added to the end result. This result is the output message list. For more details, we refer to [Gol89].
|
Input message list = { 001, 101, 110, 100 }
Output message list = { 111, 100, 110 }
|
Using this representation for individuals of a genetic algorithm, we can easily introduce the necessary operators: cross-over is performed by selecting certain bits within the classifier expressions (genes) and exchanging them with the same genes from another individual. Mutation is easily implemented by selecting a number of bits and simply changing them to something else. The technique of using entire classifier systems as individuals within a genetic program is referred to as the Pittsburgh approach [Smi]. In comparison, the Michigan approach [LF93] treats every classifier- rule as an individual. After having introduced genetic algorithms and classifier systems we will now proceed with discussing reinforcement learning algorithms.
THE APPROACH WE WILL USE to learn how to keep Petri-nets alive will be based on a reinforcement learning technique. Therefore, we will now introduce what a reinforcement learning technique is. Reinforcement learning [SAG98,KLAPM96] is originally an on-line technique where a learner tries to maximize the accumulated reward it receives from the environment. The actions the learner can take in a given situation are initially unknown, so the learner itself needs to discover a good way of working. The typical challenge for a reinforcement learning algorithm is that actions taken in a certain context will influence the future environment and rewards the learner will get.
Typical to the class of reinforcement learning algorithms is that it is defined based on the problem at hand. Reinforcement learning is defined as a solution to the problem in which a learner, which interacts with its environment, tries to reach a certain goal. Such a learner should be emerged in the environment, it should be able to sense the environment and it should be able to act upon the environment. The goal, or goals of such a problem should also be related to and expressible in the environment. A more formal definition of the problem in a more formal way will be given in section 4.4.4.
There are many kinds of reinforcement learning algorithms. For this
dissertation, we will focus on one particular branch of algorithms,
called ![]() -learners [Sut88,Tes92,SAG98].
The following sections will discuss this branch of algorithms in more
detail. We will first introduce the elements most often encountered
in reinforcement learners, second we will state the difference between
episodic and continual tasks. Third, we will formally express the
requirements of a reinforcement learning problem by means of Markov
Decision Processes. Fourth, we will explore the value function and
policy of a
-learners [Sut88,Tes92,SAG98].
The following sections will discuss this branch of algorithms in more
detail. We will first introduce the elements most often encountered
in reinforcement learners, second we will state the difference between
episodic and continual tasks. Third, we will formally express the
requirements of a reinforcement learning problem by means of Markov
Decision Processes. Fourth, we will explore the value function and
policy of a ![]() -learner. Fifth we will discuss the tradeoff
between exploration and exploitation.
-learner. Fifth we will discuss the tradeoff
between exploration and exploitation.
A typical reinforcement learning algorithm contains 4 elements:
In general, a reinforcement learning algorithm works on-line, i.e. emerged in the environment, without supervision. There is never an explicit training phase that teaches how the algorithm should behave in a real environment. However sometimes the same learner will be allowed multiple trials, in the form of episodes, to perform a task. An episode is the run of a learner until a terminal state is reached. Such a terminal state can be either a dead-state or a goal-state. After reaching such a state, a new episode starts, in which the same exact problem as before needs to be solved. However, during every episode the learner will be able to develop its behavior further until a suitable approach has been reached. Such a task is called an episodic task.
Other learning-tasks don't have terminal states and simply require the learner to maximize the total amount of reward it receives in the long run. Such a task is called a continual task.
Given the above general description of a reinforcement learning problem, we can now formally introduce the elements of a reinforcement learning algorithm. In chapter 9, we will use this formal approach to map the liveness problem to a reinforcement learning problem.
The action a learner takes at time ![]() will be called
will be called ![]() The
actions available to the learner in a situation
The
actions available to the learner in a situation ![]() are denoted
are denoted ![]() .
When an action
.
When an action ![]() is executed the resulting situation is denoted
is executed the resulting situation is denoted
![]() . The reward received after executing
. The reward received after executing ![]() is a numerical
value
is a numerical
value ![]() Time is considered to be discrete.
Time is considered to be discrete.
A reinforcement learner can never take all possible information into account when deciding upon its action, because either a) not all information is available, or b) it would require too much space to store all information. Therefore reinforcement learners require the environment to offer just enough information for the learner such that it can proceed. The situation-signal a learner receives should summarize in a compact way the past which has lead to this situation, such that no relevant information has been lost. If the state-signal succeeds in retaining this information it is said to have the Markov-property. For example, a checkers position, containing the position of all pieces on board, has the Markov-property, because it summarizes the past in a way such that no necessary information is lost for the future.
Formally, if the situation-signal has the Markov-property, the next
situation and reward can be probabilistically expressed in terms of
the current situation and reward. In the equation below ![]() denotes
a probability distribution.
denotes
a probability distribution.
This notation denotes a chance that ![]() and
and ![]() if both
if both ![]() and
and ![]() are given. In summary, a problem needs
to have the Markov property before it can be considered to be a reinforcement
learning problem.
are given. In summary, a problem needs
to have the Markov property before it can be considered to be a reinforcement
learning problem.
We will now describe the value functions ![]() ,
, ![]() and policy
and policy
![]() as used by many reinforcement learners. A policy describes
which action is favored in a given situation. To decide this, the
policy uses a value-function, which describes the maximum possible
reward a certain action could lead to. Typically, both the policy
and the value function change over time. The policy balances the exploration
and exploitation phases while the value function learns how good it
is to be in a certain state.
as used by many reinforcement learners. A policy describes
which action is favored in a given situation. To decide this, the
policy uses a value-function, which describes the maximum possible
reward a certain action could lead to. Typically, both the policy
and the value function change over time. The policy balances the exploration
and exploitation phases while the value function learns how good it
is to be in a certain state.
Formally, given a certain situation, the policy decides the probability
of an action to be chosen: ![]() returns the probability
that
returns the probability
that ![]() if
if ![]() . The value function defines what the
maximum future reward will be given a certain policy. However, because
the time a learner might run can be infinite, the expected future
reward may be also be infinite. Therefore, a discount factor is introduced
which makes future rewards less interesting if they are placed further
in the future.
. The value function defines what the
maximum future reward will be given a certain policy. However, because
the time a learner might run can be infinite, the expected future
reward may be also be infinite. Therefore, a discount factor is introduced
which makes future rewards less interesting if they are placed further
in the future.
where ![]() .
.
Given this definition of a future reward, we can define the state-value
function, which defines how good it is for a learner to be in a certain
state. Of course, this depends on which actions the learner will take
in certain situations, hence the policy ![]() should be taken into
account.
should be taken into
account.
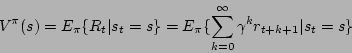
In the above equation, ![]() denotes the expected return
value given that the learner follows policy
denotes the expected return
value given that the learner follows policy ![]() . Similarly, we
can define the expected return the learner receives when it takes
action
. Similarly, we
can define the expected return the learner receives when it takes
action ![]() in state
in state ![]() .
.
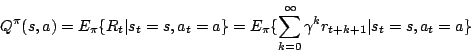
![]() is called the action-value function under policy
is called the action-value function under policy
![]() .
.
Both the state-value as action-value functions cannot be calculated
immediately because the expected future reward ![]() is unknown.
The goal of most reinforcement learning algorithms is to find approximations
of these value-functions. In chapter 9 we will
investigate how we can map the liveness problem (and our solution)
to a function approximation of
is unknown.
The goal of most reinforcement learning algorithms is to find approximations
of these value-functions. In chapter 9 we will
investigate how we can map the liveness problem (and our solution)
to a function approximation of ![]() .
.
The difference between the policy and the value-function is that a value-function estimates what future reward could be possible, while the policy decides which action will effectively be taken. However, this action is not always necessarily the action that will lead to the highest reward. If the best action is taken, the policy is exploiting the value-function, otherwise it is exploring the environment. A tradeoff between exploitation and exploration must be made. If a learner exploits too much it will be blind to possibly better solutions which could result in higher rewards, while a learner which keeps on exploring the environment in a fully random way will end up accumulating very little reward.
An action selection method in which all information is exploited without
ever trying new paths is called a greedy action selection strategy.
The drawback of such a method is clearly that it gets easy stuck in
sub-optimal solutions. A simple but effective variant of greedy action
selection methods are the ![]() -action selection methods, in
which most of the time the best available action is favored, but in
-action selection methods, in
which most of the time the best available action is favored, but in
![]() % of the time an action is uniformly random selected
from the set of possible actions. Eventually, all possible actions
will be selected once by this method.
% of the time an action is uniformly random selected
from the set of possible actions. Eventually, all possible actions
will be selected once by this method.
This wraps up our introduction of reinforcement learning.
IN THIS SECTION we have explained that we need an on-line adaptive learning algorithm that works on symbolic input and output. The algorithm needs to work on-line because of the nature of open distributed systems. The algorithm needs to work with symbolic input and output because of the nature of interfaces. The internal representation however can be either numerical or symbolic. As a result the only algorithm suitable to do the job is reinforcement learning, for which we explained the basic operation.
Second, in this chapter we introduced the use of genetic algorithms as a means to test the representation of a system, instead of an approach to solve a problem. If a certain problem can be solved easily under a certain representation, it is a good representation. If the same genetic algorithm has more trouble finding a solution the representation might not be so suitable. On the same representational track we also introduced classifier systems because we will investigate their usefulness chapter 11.
Third, we introduced the working of reinforcement learning algorithms. We explained the policy-function, value-function, reward function and the requirements posed upon a problem before it can be considered to be a reinforcement learning problem. One of these requirements was that the environment signal should summarize the past in such a way that no necessary information is lost. This property is called Markov. In chapter 9 we will need this property to ensure that the approach we use is indeed a valid reinforcement learning problem. The reinforcement learning technique introduced in this chapter will be used to create the liveness module.
We have now presented the preliminaries of this dissertation. In chapter 2 we explained the event based system we will use. In chapter 3 we introduced the use of Petri-nets as a means to formally specify an interface and in chapter 4 we introduced the learning algorithms we will need later on. Given these preliminaries we are now able to shift our attention to the case we will use to validate our thesis: concurrency strategy conflicts in open distributed systems.