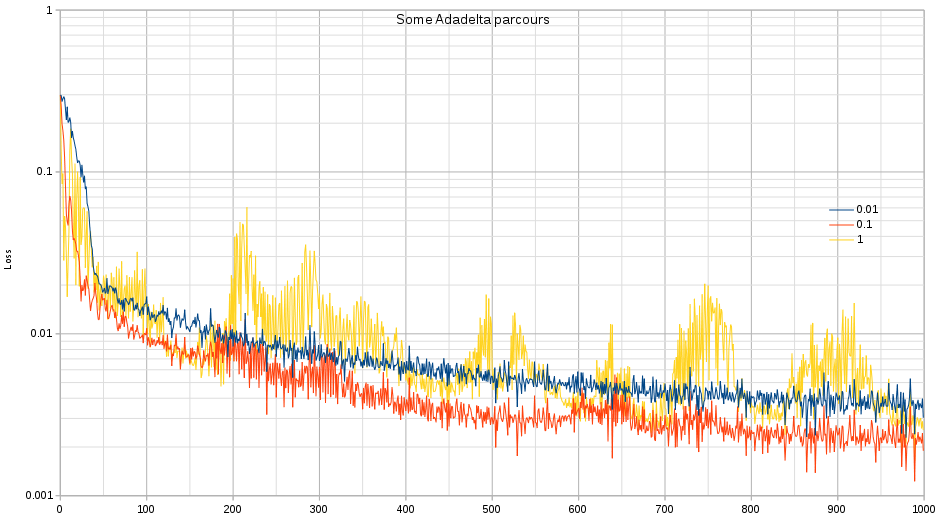
I just tested adadelta on the superresolution example that is part of the pytorch examples. The results are quiet nice and I like the fact that LeCun’s intuition to use the hessian estimate actually got implemented in an optimizer (I tried doing it myself but couldn’t get through the notation in the original paper).

Interesting is that the ‘learning-rate of 1’ will scatter throughout the entire space a bit more than what you would expect. Eventually it does not reach the same minima as a learning rate of 0.1.

In the above example we also delineated each epoch every 20 steps. That means, when step%20==0 we cleared all the gradients. Which feelsd a bit odd that we have to do so. In any case, without the delineation into epochs the results are not that good. I do not entirely understand why. It is clear that each epoch allows the optimizer to explore a ‘new’ direction by forgetting the garbage trail it was on, and in a certain way it regularizes how far each epoch can walk away from its original position. Yet _why_ the optimizer does not decide for itself that it might be time to ditch the gradients is something I find interesting.