Can an autoencoder learn the identity mapping ? To test that, I went to the extreme: let an optimalisation algorithm (SGD) find the best mapping when then visible units are 0-dimensional (a scalar) and the hidden units as well.

the first remarkable thing is that there is no solution that will have the perfect mapping ! There simply does not exist a relation that will map the input straight to the output when tied weights and sigmoids are used.

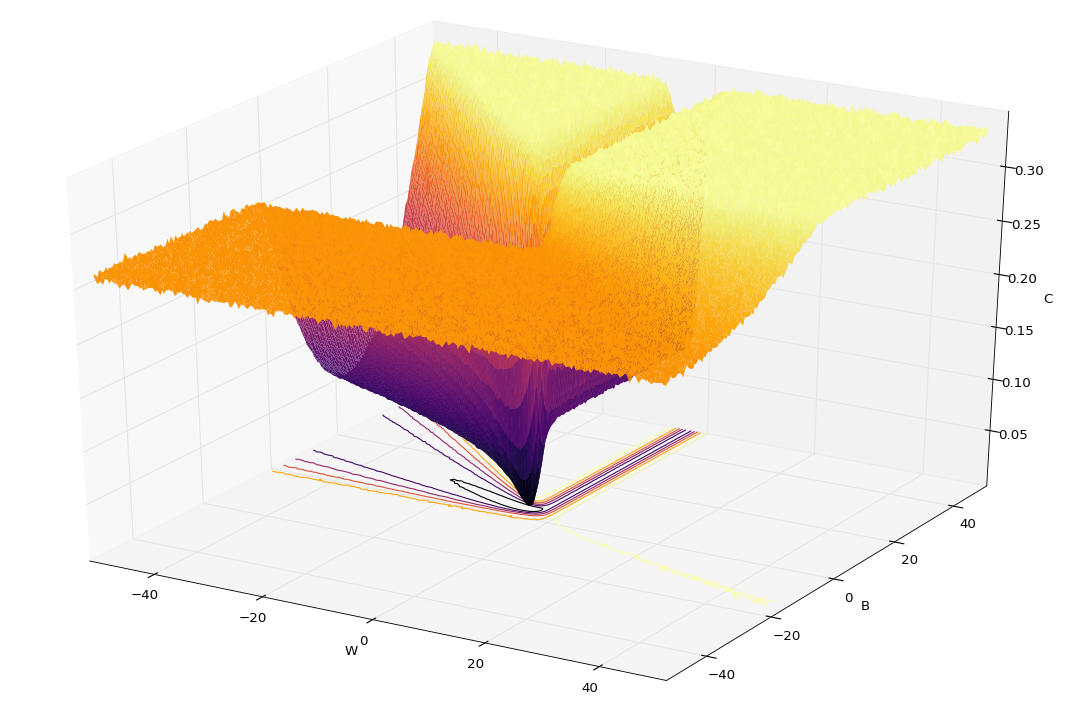
Anyway, because the problem is so non-dimensional, we can calculate the cost over an area and plot it in a surface. Two things are worth noting.

1. The minimum can be found as soon as we get into a very narrow valey… from the right angle… If we were to enter it from the back (B>40) then the value floor is not sufficiently steep to guide us quickly to the minimum.
2. If we were dropped on this surface at (W:40;B:-20) then the search algorithm would go down from one plateau to the next, blissfully aware of that nice crevasse that we laid out for it.